Автоматика.
    Автоматизация.
        Электротехнические
            комплексы и системы.

УДК 681.3

СОВОКУПНЫЕ КОЛИЧЕСТВЕННЫЕ ОЦЕНКИ КАЧЕСТВА

ВЫДЕЛЕНИЯ РЕГИОНОВ ИЗОБРАЖЕНИЙ

С ПОМОЩЬЮ СТАТИСТИЧЕСКИХ АЛГОРИТМОВ

Вовк О.Л.

            Введение

Эффективные алгоритмы выделения регионов (однородных областей) изображений применяются для обработки изображений различной природы (космических, микроскопических или снятых на обычную цифровую камеру) в тех случаях, когда стоит задача описания изображения не как матрицы пикселей, а как множества объектов, характеризующихся цветовыми, текстурными и (или) пространственными признаками. Наиболее активно научные исследования алгоритмов такого рода ведутся в следующих областях компьютерного зрения [1]: контекстный поиск изображений в базах данных, медицинская диагностика, удаленное наблюдение.

            Существует две основные группы методов автоматического распознавания регионов изображений – статистические методы [1, 2]  и методы, основанные на выделении перепадов яркости [3].          При распознавании регионов с помощью статистических методов набор пикселей изображения рассматривается как набор объектов, заданных цветовыми характеристиками, согласно которым происходит классификация (кластеризация) пикселей на группы (регионы, кластеры) с “близкими” характеристиками [4]. При кластеризации путем выделения перепадов яркости проблема выделения границ объектов решается путем локализации на изображении резких перепадов яркостной составляющей цвета [3]. С этой целью вычисляется градиент функции интенсивности в каждой точке изображения, после чего подавляются значения, не превышающие установленного порога. За основу принято брать метод Собеля.

Кроме основных групп методов разбиения изображений на регионы, в последнее время все больше разработок ведется в сфере нечеткой кластеризации изображений [5, 6]. Методы нечеткой кластеризации предполагают представление классифицируемых объектов в виде нечетких множеств и вводят функции принадлежности этим множествам, на основании которых определяют шаблоны в тот или иной кластер.

Цель данной статьи – оценить качество кластеризации изображений с помощью статистического иерархического агломеративного алгоритма, разработанного автором статьи и описанного в [4], в сравнении с наиболее распространенным алгоритмом противоположной статистической группы методов кластеризации – k-means алгоритмом (модификация которого для распознавания однородных областей изображений приведена в [7]). Исходя из поставленной цели, работа содержит следующие основные разделы:

-         краткое описание основных направлений статистической кластеризации;

-         введение оценок эффективности выделения регионов изображений;

-         анализ результатов экспериментов оценок качества процедур статистической кластеризации.

Статистическая кластеризация изображений

Постановка задачи кластеризации

Кластеризация [8] – общее название множества вычислительных процедур, используемых при создании классификации объектов. В результате кластеризации образуются “кластеры” (регионы, области) – группы похожих по различным характеристикам объектов. Кластерный метод [8] – многомерная статистическая процедура, выполняющая сбор данных, содержащих информацию о характеристиках объектов, и затем упорядочивающая объекты в сравнительно однородные группы.

Исходные данные для процедуры кластеризации – набор объектов, каждый из которых задается вектором своих характеристик. В ходе кластеризации происходит объединение “подобных” объектов в отдельные классы. Результатом кластеризации является набор классов, содержащих однородные объекты [8].

В случае решения задачи выделения объектов изображения задан набор пикселей, каждый из которых определяется тремя цветовыми компонентами в одном из цветовых пространств. С помощью процедуры кластеризации осуществляется выделение групп пикселей, имеющих наиболее “близкие” цветовые компоненты, т.е. происходит распознавание изображений.

            Примеры выделения регионов (кластеров) изображений приведены на рис. 1.

Рис. 1 Примеры кластеризации (выделения регионов) изображений

Основные технологии статистической кластеризации

Согласно [1, 2] существует две базовые технологии статистической кластеризации объектов: иерархическая и итеративная.

            Иерархические методы представляют собой процедуры создания последовательности вложенных разбиений, исходя из данных матрицы близости [1].

Формально любой иерархический метод кластеризации состоит из следующих шагов [2]:

1.                  Расчет матрицы близости между всеми парами шаблонов. Изначально каждый объект – отдельный кластер.

2.                  Нахождение минимума в матрице близости и объединение кластеров с минимальным расстоянием. Обновление строк и столбцов матрицы, соответствующих объединенным кластерам.

3.    Если все объекты принадлежат одному кластеру, то конец работы метода, иначе на шаг 2.

В результате работы таких методов, все объекты классификации будут принадлежать одному кластеру. Поэтому для получения значимых разбиений необходимо рассматривать различные “срезы” построенной иерархии [1].

Основная идея итеративных методов (методов разбиения) [2] – нахождение единственного разделения шаблонов по кластерам, вместо иерархии, полученной согласно иерархическим технологиям. Реализация методов разбиения предполагает выполнение следующих шагов [1, 2]:

1.                  Выбор начального распределения объектов по кластерам. Расчет центров тяжести полученных кластеров.

2.                  Перегруппировка объектов кластеров: отнесение каждого объекта к кластеру с минимальным расстоянием до центра.

Наиболее используемым методом данной группы является метод k-means кластеризации [1, 2, 7], который при решении задачи выделения объектов изображений состоит из следующих основных этапов:

1.                  Произвольное разбиение на некоторое заданное количество кластеров (обычно изначально количество кластеров равно двум).

2.                  Вычисление центров тяжести полученных кластеров.

3.                  Анализ каждого объекта каждого кластера; и перераспределение в кластер с минимальным расстоянием до центра.

4.                  После перераспределения производится пересчёт центров тяжести кластеров.

5.                  Этапы 3, 4 повторяются до тех пор, пока все точки не будут находиться в “ближайшем кластере”.

6.                  Если не удовлетворен критерий окончания кластеризации, то увеличивается количество кластеров, повторяются шаги 1 – 5.

Необходимо отметить, что в работах группы исследователей Ванга [7] показано, что при кластеризации изображений количество кластеров необходимо ограничивать шестнадцатью –  для выделения наиболее информативных областей изображений.

            В работе [4] автором статьи предлагается новый статистический иерархический агломеративный алгоритм для выделения регионов изображений. В его основе – битовая маска связей и рангов цветовых компонентов [9], характеризующих центры кластеров. Так как любое цветовое пространство трехмерно, то разработанная маска отражает взаимосвязи и ранги трех цветовых характеристик. Она содержит 18 бит, причем 9 младших бит характеризуют взаимосвязи цветовых составляющих, а старшие 9 бит отражают уровни (ранги) каждого из анализируемых компонентов в отдельности.

При формировании младших бит маски, каждая пара компонентов анализируется на наличие связей типа: меньше, больше и равно. Старшие биты маски описывают уровни каждой из трех характеристик; вводится три основных уровня – низкий, средний и высокий. Кроме того, предлагается “размывать” границы, как отношений, так и уровней, с помощью введения некоторой погрешности маски – e.

            Разработанный иерархический алгоритм  [4] сокращенно можно описать тремя основными стадиями:

1.                  Этап полной связи. Предполагается, что изначально каждый пиксель изображения представляет собой отдельный кластер; на этом этапе происходит разнесение точек изображения с различными битовыми масками в различные кластеры. Т.е. для каждого пикселя изображения формируется маска взаимосвязей и рангов, затем пиксели с одинаковыми масками разносятся в разные кластеры.

2.                  Этап одиночной связи. Для полученных на предыдущем этапе кластеров строится матрица близости (расстояний) между кластерами. В качестве расстояния между кластерами используется среднее Евклидово расстояние между всеми парами точек, входящих в кластеры, расстояние между которыми рассчитывается. В полученной матрице происходит поиск наиболее “близких” кластеров (т.е. кластеров с минимальным расстоянием), которые объединяются, образуя новые кластеры, для которых производится перерасчет центров. Причем, кластеры i-ый и j-ый считаются “близкими” только в том случае, если расстояние от i-ого кластера к j-ому является минимальным в i-ой строке матрицы близости и расстояние от j-ого кластера к i-ому является минимальным в j-ой строке матрицы близости. Из матрицы расстояний удаляются строки и столбцы, соответствующие объединенным кластерам, и добавляется строка и столбец, соответствующие полученному кластеру. Данный этап повторяется до тех пор, пока количество кластеров не достигнет количества шестнадцати (данный числовой параметр взят из работы [7] и проверен экспериментально).

3.                  Этап окончания. Данный этап разработан как критерий окончания кластеризации; он аналогичен предыдущему этапу с некоторым ограничением. Объединение кластеров с минимальным расстоянием матрицы близости производится только при выполнении  условия “близости” масок; в противном случае процесс кластеризации заканчивается.

Совокупные количественные оценки эффективности выделения кластеров изображений

Рассмотрим три наиболее распространенные оценки качества выделения регионов изображений [10].

            Харалик и Шапиро ввели оценку качества результатов выделения регионов изображений, основанную на следующих критериях [10, 11]: 1) выделенные регионы должны быть однородными; 2) внутренняя часть области должна быть простой, без большого числа отверстий; 3) смежные регионы должны иметь значительно отличающиеся значения соответствующих цветовых характеристик. Согласно предложенным критериям, оценочная функция определяется как:

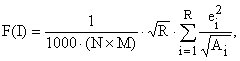                                    (1) 

где: I – изображение, разбитое на кластеры; N´M – размер изображения; R – число выделенных регионов;  A_i и e_i – площадь и среднее отклонение цветовых характеристик для i-ого региона соответственно. При анализе эффективности сравниваемых способов кластеризации, минимальные значения показателей (1) соответствуют наилучшему методу разбиения изображения на регионы.

            Оценка (1) состоит из трех основных частей, входящих в формулу в качестве множителей произведения: первая часть – нормализующий фактор, обратно пропорциональный размеру изображения; вторая часть, , “препятствует” выделению большого числа кластеров; третья часть, сумма, увеличивает значение оценочного показателя в случае выделения неоднородных регионов.

            В работе [12] предлагается модификация оценки качества распознавания регионов изображений (1), которая, как подчеркивают авторы, более точно соответствует визуальному восприятию результатов кластеризации:

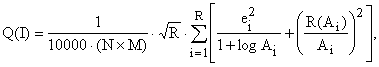                      (2)

где R(A_i) – количество регионов, имеющих площадь, равную A_i.

            Критерий Q(I) (2) отличается от критерия F(I) (1) третьим компонентом, суммой, первая из частей которой “препятствует” образованию неоднородных кластеров, а вторая – выделению большого числа маленьких регионов одинакового размера.

            В качестве другого подхода к оценке результатов кластеризации изображений в [10] выделяют технологию нахождения оптимального разбиения изображений на кластеры по цветовому подобию, подробно описанную в [13]. В основании рассматриваемой методики – минимизация следующего функционала качества:

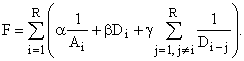                                  (3)

В формуле (3): D_i – среднее расстояние между цветовыми характеристиками i-ого региона, D_i-j – среднее расстояние между цветовыми компонентами i-ого и j-ого регионов, a, b, g - контрольные параметры, соответствующие уровню приоритета того или иного компонента критерия (3).

Результаты экспериментальной оценки качества кластеризации изображений

Проведем экспериментальное сравнение разработанного автором алгоритма статистического иерархического агломеративного алгоритма (СИАА) кластеризации [4] с k-means алгоритмом [1,2,7] по критериям (1)-(3). В качестве анализируемой базы данных изображений используется коллекция 24-битных семантически классифицированных изображений, разработанная исследовательской группой Ванга [14].

Результаты экспериментов сравнения по критерию Харалика и Шапиро (1) представлены на рис. 2, по критерию (2) – рис. 3, по критерию (3) – рис.4. В качестве контрольных параметров критерия (3) выбраны следующие значения: a=b=g=1 (все компоненты критерия равнозначны). Необходимо отметить, что оценка качества кластеризации проводилась при выделении обоими алгоритмами одинакового количества кластеров; в качестве ошибок по каждому из критериев приводится среднее значение F(I), Q(I), F среди всех значений ошибок изображений с энтропией в определенных диапазонах. Кроме того, в анализируемой базе данных различное число изображений попадают в каждый из рассматриваемых интервалов энтропии (процент изображений, энтропия которых принадлежит каждому из анализируемых интервалов – см. таблица 1).

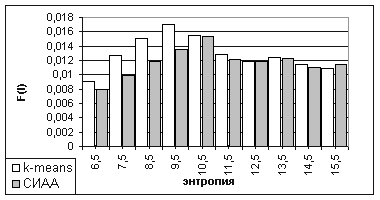Рис. 2 Экспериментальная оценка качества кластеризации, критерий F(I) (1)

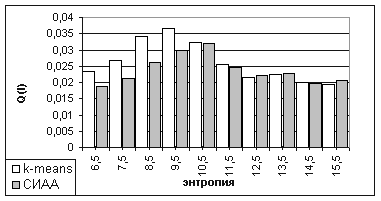Рис. 3 Экспериментальная оценка качества кластеризации, критерий Q(I) (2)

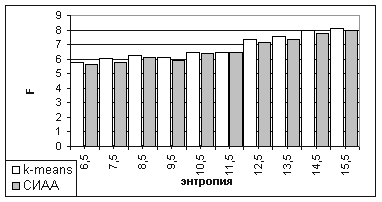Рис. 4 Экспериментальная оценка качества кластеризации, критерий F (3)

Таблица 1

            Рассматривая полученные результаты, можно сделать следующие выводы:

-                     для изображений с небольшими показателями энтропии [6…10] авторский алгоритм значительно превосходит статистический алгоритм кластеризации k-means по критериям F(I), Q(I);

-                     для изображений с высокими показателями энтропии (10…16) анализируемые алгоритмы кластеризации имеют приблизительно одинаковый уровень ошибок согласно критериям F(I), Q(I);

-                     при анализе алгоритмов согласно критерию нахождения оптимального разбиения согласно цветовому подобию F предлагаемый автором алгоритм превосходит k-means алгоритм на всех рассмотренных интервалах энтропии для коллекции изображений Ванга [14].

Такие результаты можно обосновать тем, что при применении k-means алгоритма для кластеризации изображений не учитываются особенности кластеризируемых объектов (пикселей изображений), а  в  основе  авторского алгоритма – битовая маска взаимосвязей и рангов цветовых компонентов пикселей. 

Заключение

Выделение значимых областей изображений – актуальная задача как для исследователей в области компьютерного зрения, так и для исследователей в области разработки эффективных механизмов поиска изображений. Однако, на сегодняшний день не разработано универсального критерия для оценки качества кластеризации изображений.

В данной работе рассматриваются основные способы оценки качества выделения регионов изображений по цветовому подобию, и приводится сравнение разработанного автором статистического иерархического агломеративного алгоритма с наиболее используемым среди статистических алгоритмов k-means алгоритмом.

Результаты экспериментального сравнения показывают более высокий уровень качества кластеризации изображений иерархическим агломеративным алгоритмом по сравнению с k-means алгоритмом.

В качестве направления дальнейшего исследования предлагается разработка эффективного механизма контекстного поиска кластеризованных изображений.

1.                  Chen C.H., Pau L.F., Wang P.S.P. The Handbook of Pattern Recognition and Computer Vision (2^nd Edition). –  World Scientific Publishing Co., 1998. –  1004 p.

2.                  Jain A.K., Murty M.N., Flynn P.J. Data Clustering: A Review // ACM Computing Surveys. – 1999. – vol. 31, №3. – P. 264-323.

3.                  Байгарова Н.С., Бухштаб Ю.А., Евтеева Н.Н. Современная технология содержательного поиска в электронных коллекциях изображений. – Институт прикладной математики им. М. В. Келдыша РАН, http://artinfo.ru/eva/ eva2000M/eva-papers/200008/Baigarova-R.htm.

4.                  Вовк О.Л. Иерархический  агломеративный  алгоритм  кластеризации для выделения регионов изображений // Графикон’2004. – Москва, 2004, http://www.graphicon.ru/2004.

5.                  Baraldi  A., Blonda  P. A Survey of  Fuzzy Clustering Algorithms for Pattern  Recognition – Part I // IEEE  Transactions on systems, man, and cybernetics – Part B: Cybernetics. – 1999. –  vol. 29, №6. –  P. 778-785.

6.                  Xie X.L., Beni G. A validity measure for fuzzy clustering // IEEE Transactions on Pattern Analysis and Machine Intelligence. –  1991. – P. 841-847.

7.                  Wang J. Z., Du Y. Scalable Integrated Region-based Image Retrieval using IRM and Statistical Clustering // Proc. ACM and IEEE Joint Conference on Digital Libraries. –  Roanoke, VA, ACM, June 2001. – Р. 268-277.

8.                  Ким Д. О., Мьюллер Ч. У., Клекка У. Р. Факторный, дискриминантный и кластерный анализ. – М.: Финансы и статистика, 1989. – 215 с.

9.                  Вовк О.Л. Битовая маска взаимосвязей и рангов для ускорения и автоматизации статистической кластеризации // САИТ’2004. – Киев, 2004. – С. 17-18.

10.              Schettini R., Ciocca G., Zuffi S. A Survey of Methods for Color Indexing and Retrieval in Image Databases, http://www.itim.mi.cnr.it/Linee/Linea1/scaricare/methodsCIIR-9-1-01a.pdf

11.              Haralick R.H., Shapiro L.G. Image Segmentation Techniques // Computer Vision, Graphics and Image Processing. – 1985. – vol. 29. – P.100-132.

12.              Borsotti M., Campadelli P., Schettini R. Quantitative evaluation of color image segmentation results // Pattern Recognition Letters. – 1998. – vol. 19. – P.741-747.

13.              Del Bimbo A. Visual Information Retrieval. – San Francisco: Morgan Kaufmann Publishers, 1999.

14.              База данных изображений, http://wang.ist.psu.edu/~jwang/test1.tar.