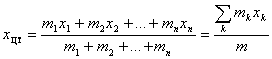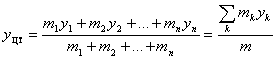УДК 620.179:534.6
ЛОКАЛИЗАЦИЯ МЕСТА ПОЛОЖЕНИЯ СКВОЗНЫХ ДЕФЕКТОВ ПО СИГНАЛАМ АКУСТИЧЕСКОЙ ЭМИССИИ
Бабак В.П., Пономаренко А.В.
Введение
Для обнаружения и локализации сквозных дефектов, образовавшихся в протяженных продуктопроводах под давлением, доступ к которым ограничен (расположение в земле на определенной глубине или каналах, наличие защитных слоев и т.д.), распространение получили низкочастотный акустический метод и метод акустической эмиссии [1-6]. Первый основан на анализе взаимной корреляционной функции (ВКФ) при обработке низкочастотных акустических сигналов, регистрируемых двумя датчиками, между которыми находится источник излучения [1-3]. При этом расстояние до места утечки среды рассчитывается по временной задержке прихода сигналов на датчики, определяемой по ВКФ, а именно по временному положению максимума амплитуды ВКФ. При использовании метода акустической эмиссии (АЭ) применяются два основных подхода.
В основе второго подхода, лежит расчет координат утечки по амплитудам сигналов АЭ, регистрируемых несколькими датчиками, установленными на объекте контроля [5, 7]. Количество датчиков всегда должно быть больше двух. При этом в качестве амплитуды сигналов непрерывной АЭ используется наиболее вероятная амплитуда ![]() [8]. Если известно значение коэффициента затухания
[8]. Если известно значение коэффициента затухания ![]() в материале изделия, а затухание происходит по экспоненциальному закону, то по значениям амплитуд определяются разности расстояний [5, 7] до каждой пары датчиков в виде
в материале изделия, а затухание происходит по экспоненциальному закону, то по значениям амплитуд определяются разности расстояний [5, 7] до каждой пары датчиков в виде ![]() , где
, где ![]() - разность расстояний от источника сигналов АЭ до i-го датчика;
- разность расстояний от источника сигналов АЭ до i-го датчика; ![]() - значения для наиболее вероятных амплитуд с i-го и j-го датчиков;
- значения для наиболее вероятных амплитуд с i-го и j-го датчиков; ![]() - коэффициент затухания. В общем случае для любых пар датчиков записывается уравнение в вида
- коэффициент затухания. В общем случае для любых пар датчиков записывается уравнение в вида ![]()
![]() , где x, y – координаты неизвестного источника излучения;
, где x, y – координаты неизвестного источника излучения; ![]() - координаты выбранной пары приемных датчиков. Решение систем уравнений, составленных для выбранных пар датчиков, например, при известных координатах трех или четырех датчиков [5, 7], позволяет определить координаты (x, y) местоположения течи на изделии.
- координаты выбранной пары приемных датчиков. Решение систем уравнений, составленных для выбранных пар датчиков, например, при известных координатах трех или четырех датчиков [5, 7], позволяет определить координаты (x, y) местоположения течи на изделии.
Второй подход, как и в случае низкочастотного метода, основан на анализе ВКФ при обработке сигналов АЭ, поступающих на два датчика [6], между которыми находится сквозной дефект. Однако в отличие от низкочастотного метода полоса частот анализируемых сигналов в методе АЭ имеет значительно больший диапазон значений.
Методика, основанная на анализе ВКФ, является более простой. Однако наличие различных влияющих факторов (акустические шумы, неравномерность физико-механи-ческих характеристик материалов, дефекты структуры и т.д.) проявляется в сложном характере изменения ВКФ, невыразительности и неустойчивости основного всплеска ВКФ. Следствием этого может быть существенная вариация результатов измерений. Вопросы повышения достоверности поиска утечек рассмотрены в ряде работ [9-11], где показана возможность использования частотной фильтрации и волновой (пространственной) селекции. Их применение направлено на получение статистически устойчивого основного всплеска ВКФ. В тоже время, из-за наличия сложного, комбинированного сочетания влияющих факторов, возможно изменение положения максимума в пределах основного всплеска ВКФ. При таких условиях расчет расстояния по временному положению максимума ВКФ может приводить к ошибкам обнаружения течи.
В работе будет рассмотрена методика определения расстояния до течи с использованием анализа ВКФ. Будет показано, что снижение действия факторов, влияющих на искажение формы основного всплеска ВКФ, и, как следствие, повышение достоверности определения расстояния до течи, обеспечивается за счет обработки временного положения центра тяжести основного всплеска ВКФ.
Результаты исследований
Как было отмечено выше, определение расстояния до течи с использованием ВКФ осуществляется по временной задержке прибытия сигналов поступающих на два датчика, расположенных на конструкции, по выражению вида
![]() , (1)
, (1)
где L – расстояние между датчиками; ![]() - скорость распространения сигналов по объекту контроля (низкочастотных сигналов или сигналов АЭ);
- скорость распространения сигналов по объекту контроля (низкочастотных сигналов или сигналов АЭ); ![]() - временная задержка или разность прихода сигналов на датчики.
- временная задержка или разность прихода сигналов на датчики.
Выражение (1) правомочно при условии, что один из датчиков является базовым, относительно которого и определяется расстояние до течи. При этом значение ![]() определяется по ВКФ
определяется по ВКФ ![]() сигналов от датчиков
сигналов от датчиков ![]() и
и ![]() , например, исходя из условия
, например, исходя из условия
![]() . (2)
. (2)
Другими словами, величина ![]() определяется по временному расстоянию (положению) до максимума основного всплеска ВКФ. Вместе с тем, основной всплеск на корреляционной функции относительно оси времени можно рассматривать, как импульсный сигнал, по параметрам которого определяется
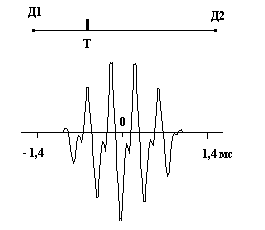
определяется по временному расстоянию (положению) до максимума основного всплеска ВКФ. Вместе с тем, основной всплеск на корреляционной функции относительно оси времени можно рассматривать, как импульсный сигнал, по параметрам которого определяется ![]() . Поэтому, если какая-либо анализируемая величина определяется “расстоянием“ до не перекрывающегося сигнала, то крайне важно установить точное значение данного “расстояния”. Другими словами, возникает вопрос: какую точку в общей форме сигнала взять за точку отсчета? Традиционно данная точка для ВКФ определяется, в соответствие, с соотношением (2), т.е. по максимальной амплитуде ВКФ. При этом предполагается, что максимум основного всплеска на корреляционной функции является статистически устойчивым. Однако, как отмечалось выше, наличие большого количества влияющих факторов приводит к искажению формы ВКФ, и, прежде всего, интересующего нас, его основного всплеска (рис.1). В тоже время, пик основного всплеска может быть размытым (иметь полочку), а в его пределах наблюдается перемещение положения максимальной амплитуды. Как показывают расчеты, например, для данных приведенных на рис.1, при расстоянии между датчиками 1,64 м, расположении источника излучения на расстоянии 0,53 м от датчика 1 (Д1, рис1), изменение временного положения максимальной амплитуды в пределах основного всплеска приводит к ошибке определения места положения источника, которая может достигать 20%.
. Поэтому, если какая-либо анализируемая величина определяется “расстоянием“ до не перекрывающегося сигнала, то крайне важно установить точное значение данного “расстояния”. Другими словами, возникает вопрос: какую точку в общей форме сигнала взять за точку отсчета? Традиционно данная точка для ВКФ определяется, в соответствие, с соотношением (2), т.е. по максимальной амплитуде ВКФ. При этом предполагается, что максимум основного всплеска на корреляционной функции является статистически устойчивым. Однако, как отмечалось выше, наличие большого количества влияющих факторов приводит к искажению формы ВКФ, и, прежде всего, интересующего нас, его основного всплеска (рис.1). В тоже время, пик основного всплеска может быть размытым (иметь полочку), а в его пределах наблюдается перемещение положения максимальной амплитуды. Как показывают расчеты, например, для данных приведенных на рис.1, при расстоянии между датчиками 1,64 м, расположении источника излучения на расстоянии 0,53 м от датчика 1 (Д1, рис1), изменение временного положения максимальной амплитуды в пределах основного всплеска приводит к ошибке определения места положения источника, которая может достигать 20%.
Из механики известно [12], что если в плоскости дана система материальных точек M(xk,yk) с массой mk, где k=1, 2,…, n, все точки неизменно связаны между собой, а вес каждой точки ![]() есть вертикальная сила, величина которой равна
есть вертикальная сила, величина которой равна ![]() , где g – ускорение силы тяжести, одинаковое для всех материальных точек, то координаты центра тяжести этой системы определяются по выражениям
, где g – ускорение силы тяжести, одинаковое для всех материальных точек, то координаты центра тяжести этой системы определяются по выражениям
|
|
(3) |
а) б)
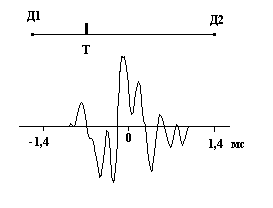
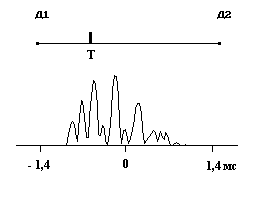
в) г)
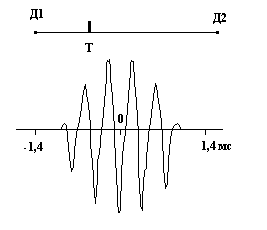
Рис. 1 ВКФ при определении места положения модельной течи: а, б – возбуждение акустичес-кого излучения периодическим низкочастотным импульсным сигналом, поступающим на пьезоке-рамический датчик возбуждения; в, г - возбуждение акустического излучения наложением периоди-ческого низкочастотного импульсного сигнала и сигнала типа белого шума, поступающих на пьезо-керамические датчики возбуждения, расположенные в близи друг от друга; г - представление ВКФ при инверсии отрицательных значений. Д1, Д2 – приемные датчики; Т – место положения источника излучения
Если пренебречь бесконечно малыми равномерно-высшего порядка, заставляя частицы (материальные точки) бесконечно уменьшаться (их число n безгранично увеличивается), то от сумм (3) переходят к интегралам.
Следует подчеркнуть, что центр тяжести есть единственный и однозначно определяемый математически. Данный факт играет немаловажное прикладное значение во многих физико-химических исследованиях, где приходится иметь дело с зависимостями (сигналами), форма которых может видоизменяться под влиянием большого количества факторов. В зависимости от области проводимых исследований сигналы и площадь под ними могут характеризовать различные величины. Так в регнтгеноструктурном анализе [13] используются сигналы, площадь которых характеризует интегральную интенсивность дифракционных линий, а для определения местоположения центра тяжести дифракционной линии производят вычисления согласно выражению
![]() , (4)
, (4)
где I – интенсивность дифракционных линий; ![]() – координаты вдоль оси углов дифракционных линий; n – число участков разбиения профиля дифракционной линии.
– координаты вдоль оси углов дифракционных линий; n – число участков разбиения профиля дифракционной линии.
Подобный подход используется и, в так называемом, методе моментов, при решении задач определении функционала положения ![]() обобщенного импульса
обобщенного импульса ![]() , т.е. при определении положения условной точки
, т.е. при определении положения условной точки ![]() по оси абсцисс внутри интервала возможных значений функции
по оси абсцисс внутри интервала возможных значений функции ![]() [14]. В общем случае, согласно данному методу, функционал положения определяется абсциссой центра тяжести
[14]. В общем случае, согласно данному методу, функционал положения определяется абсциссой центра тяжести ![]() кривой
кривой ![]() в виде
в виде
![]() . (5)
. (5)
Тогда для значений ![]() =1 и
=1 и ![]() =2 функционал (5) будет иметь вид
=2 функционал (5) будет иметь вид
![]() , (6)
, (6)
![]() . (7)
. (7)
Выражение (6) определяет центр тяжести по “площади”, а выражение (7) – центр тяжести по “энергии”. При этом, если функция![]() не является симметричной, то
не является симметричной, то ![]()
![]()
![]() .
.
Несмотря на громоздкость вычислений, преимущества такого подхода очевидны, поскольку, как было отмечено выше, центр тяжести является однозначно определяемым математически, а с использованием компьютерной техники данные вычисления не представляют трудностей.
При обработке сигналов возможно использование, как определения центра тяжести по площади, так и центра тяжести по энергии, при условии того, что выбранный центр тяжести является реперной точкой во всех проводимых измерениях. Однако, если исследуемый сигнал имеет сложную, изрезанную форму, то энергия сигнала является более емким параметром, имеющим большую чувствительность к изменению формы сигнала. Поэтому, совершенно очевидно, что более предпочтительным является определение энергетического центра тяжести, в соответствии с выражением (7).
Основной всплеск ВКФ, относительно оси времени, можно рассматривать как импульс, по параметрам которого определяется временная задержка прихода сигналов на датчики. Тогда его обработку можно осуществлять, в соответствии, с рассмотренным выше. При цифровом способе регистрации и обработки сигналов АЭ с проведением стандартных расчетов ВКФ [15], выражение (7), определяющее временное положение энергетического центра тяжести по основному всплеску ВКФ, запишется в виде
![]() , (8)
, (8)
где ![]() - k-ый отсчет амплитуды принятого сигнала в момент времени аналого-цифрового преобразования
- k-ый отсчет амплитуды принятого сигнала в момент времени аналого-цифрового преобразования ![]() ;
; ![]() -временной интервал дискретизации входного сигнала;
-временной интервал дискретизации входного сигнала; ![]() -чувствительность аналого-цифрового преобразователя на единицу младшего разряда;
-чувствительность аналого-цифрового преобразователя на единицу младшего разряда; ![]() - цифровой код k-го отсчета амплитуды на выходе аналого-цифрового преобразователя; n – количество отсчетов амплитуды на интервале действия сигнала.
- цифровой код k-го отсчета амплитуды на выходе аналого-цифрового преобразователя; n – количество отсчетов амплитуды на интервале действия сигнала.
С учетом ![]() и
и ![]() выражение (8) перепишем в виде
выражение (8) перепишем в виде
![]() =
= ![]() . (9)
. (9)
На рис.2 показан типичный основной всплеск ВКФ при обработке тестовых сигналов АЭ, возбуждаемых датчиком излучения, установленным на расстоянии 0,53 м от датчика 1 (рис.1). Амплитуда основного всплеска ВКФ представлена в относительных единицах. Обработка параметров основного всплеска ВКФ с определением временной задержки по пиковому значению его амплитуды, а так же с использованием центра тяжести по площади и энергии сигнала, с последующим определением расстояния до имитатора излучения показала следующие. Для данных, приведенных на рис.1, расстояние, определяемое по пиковому значению амплитуды ВКФ, составляет 0,5 м; с использованием центра тяжести по площади – 0,55 м; с использованием центра тяжести по энергии – 0,54 м. При этом отклонение в процентном отношении от истинного положения источника излучения составляет, соответственно: ~ 6%, ~4 % и ~ 2%.
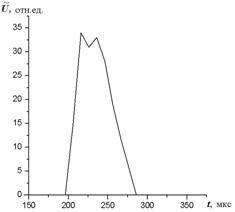
Рис. 2 Основной всплеск ВКФ при обработке тестовых сигналов АЭ. Базовым датчиком является датчик 1, в соответствии с рис.1
Из полученных результатов видно, что, во-первых, для сигнала сложной формы центр тяжести по площади не совпадает с центром тяжести по энергии. Во-вторых, ошибка определения расстояния по энергии имеет наименьшее значение – в процентном отношении почти в три раза меньше, чем по пиковому значению основного всплеска ВКФ.
Статистическая обработка результатов определения места положения источника излучения по выборкам из N=100 значений каждая с использованием пиковой амплитуды, центра тяжести по площади и центра тяжести по энергии основного всплеска ВКФ показала, что экспериментальные данные описываются нормальными законами распределения (рис. 3, рис. 4) с вероятностью, соответственно: 0,99042; 0,99855 и 0,99816.
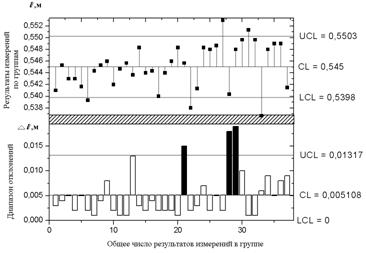
Рис. 3 Обработка результатов определения места положения источника излучения с использованием центра тяжести по энергии основного всплеска ВКФ: UCL, LCL – верхний и нижний контрольные уровни для описания закона распределения; CL – среднее значение
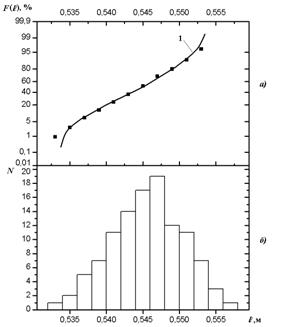
Рис. 4 Распределение по результатам определения места положения источника излучения с использованием центра тяжести по энергии основного всплеска ВКФ: а - функция распределения; б – частота; 1 – функция для идеального нормального распределения
Из анализа распределений получены оценки среднего (![]() ) и стандартного отклонения (s) места положения источника излучения, значения которых составили: при определении временной задержки по пиковой амплитуде -
) и стандартного отклонения (s) места положения источника излучения, значения которых составили: при определении временной задержки по пиковой амплитуде -![]() =0,499 м,
=0,499 м, ![]() =0,00505 м; при определении временной задержки по центру тяжести площади -
=0,00505 м; при определении временной задержки по центру тяжести площади - ![]() =0,559 м,
=0,559 м, ![]() =0,00468 м; при определении временной задержки по центру тяжести энергии -
=0,00468 м; при определении временной задержки по центру тяжести энергии - ![]() =0,545 м,
=0,545 м, ![]() =0,00486 м. Так как оценки среднего проведены для выборок из N элементов, то, в соответствии с [6], определим доверительные интервалы действительного среднего
=0,00486 м. Так как оценки среднего проведены для выборок из N элементов, то, в соответствии с [6], определим доверительные интервалы действительного среднего ![]() для заданных вероятностей в виде
для заданных вероятностей в виде
![]() , (10)
, (10)
где ![]() - коэффициент, значения которого являются табличными данными для заданных вероятностей:
- коэффициент, значения которого являются табличными данными для заданных вероятностей: ![]() =1,645 для р=0,9;
=1,645 для р=0,9; ![]() =2,0 для р=0,955;
=2,0 для р=0,955; ![]() =3,0 для р=0,997.
=3,0 для р=0,997.
Обработка экспериментальных данных, в соответствии с (10), показала, что для заданных вероятностей среднее значение места положения источника излучения ![]() при определении временной задержки по пиковой амплитуде, по центру тяжести площади и центру тяжести энергии основного всплеска ВКФ лежит, соответственно, в пределах:
при определении временной задержки по пиковой амплитуде, по центру тяжести площади и центру тяжести энергии основного всплеска ВКФ лежит, соответственно, в пределах:![]() = (0,499 ± 0,00083 )м для вероятности 0,9,
= (0,499 ± 0,00083 )м для вероятности 0,9, ![]() = (0,499 ± 0,001)м для вероятности 0,955,
= (0,499 ± 0,001)м для вероятности 0,955, ![]() = 0,499 ± 0,0015)м для вероятности 0,997;
= 0,499 ± 0,0015)м для вероятности 0,997; ![]() = (0,559 ± 0,00076 )м для вероятности 0,9,
= (0,559 ± 0,00076 )м для вероятности 0,9, ![]() = (0,559 ± 0,00094)м для вероятности 0,955,
= (0,559 ± 0,00094)м для вероятности 0,955, ![]() = (0,559 ± 0,0014)м для вероятности 0,997;
= (0,559 ± 0,0014)м для вероятности 0,997; ![]() = (0,545 ± 0,0008)м для вероятности 0,9,
= (0,545 ± 0,0008)м для вероятности 0,9, ![]() = (0,545 ± 0,00097)м для вероятности 0,955,
= (0,545 ± 0,00097)м для вероятности 0,955, ![]() = (0,545 ± 0,0015)м для вероятности 0,997. Доверительный интервал, в котором находится значение места положения источника излучения
= (0,545 ± 0,0015)м для вероятности 0,997. Доверительный интервал, в котором находится значение места положения источника излучения ![]() для заданных вероятностей, определим в виде
для заданных вероятностей, определим в виде
![]() =
=![]() ±
± ![]() . (11)
. (11)
Результаты расчетов, проведенных в соответствии с (11), приведены в табл.1.
Таблица 1
Доверительные границы на среднее значение расстояний до источника акустического излучения
|
Параметры основного всплеска ВКФ для определения временной задержки |
Доверительные границы значения места положения источника излучения |
||
|
0,9 |
0,955 |
0,997 |
|
|
Пиковая амплитуда |
0,499 ± 0,009 |
0,499 ± 0,011 |
0,499 ±0,017 |
|
Центр тяжести площади |
0,559 ± 0,0085 |
0,559 ± 0,01 |
0,559 ±0,015 |
|
Центр тяжести энергии |
0,545 ± 0,0088 |
0,545 ± 0,011 |
0,545 ±0,016 |
Из полученных результатов видно, что при истинном расположении источника излучения на расстоянии 0,53 м от базового датчика ошибка определения его положения по параметрам основного всплеска ВКФ составляет: при использовании пиковой амплитуды – 5,85%; при использовании центра тяжести по площади – 5,5%; при использовании центра тяжести по энергии – 2,8%.
Заключение
Таким образом, результаты проведенных исследований показали, что при регистрации и обработки сигналов акустической эмиссии для определения места положения источника излучения возможно использовании двух подходов. Первый из них, основан на обработке наиболее вероятных амплитуд сигналов, регистрируемых несколькими датчиками при известном коэффициенте затухания звука в материале. Второй - на определении временной задержки по положению пиковой амплитуды основного всплеска ВКФ. Однако сложность формы ВКФ и ее основного всплеска приводят к значительным ошибкам в определении места положения источника излучения (течи). Для уменьшения ошибок измерений используют различные способы, направленные на получение статистически устойчивого основного всплеска ВКФ. В тоже время, для точки отсчета временной задержки по основному всплеску ВКФ возможно использовать и другие параметры, которые имеют однозначное математическое определение. К таким параметрам относятся: центр тяжести площади основного всплеска ВКФ и его энергетический центр тяжести. Статистический анализ данных по определению места положения источника тестового излучения с использованием пиковой амплитуды, центра тяжести площади и центра тяжести энергии основного всплеска ВКФ показал, что наименьшая ошибка возникает при использовании центра тяжести по энергии. При этом ошибка уменьшается практически в два раза по отношению к определению временной задержки по пиковой амплитуде и по центру тяжести площади основного всплеска ВКФ.
The outcomes of researches using of acoustic emission are adduced at a fix of through defects position in pipeline, that working under pressure. Is showing, that the definition a dwell of coming a signals from antenna sensors is possible with using a parameters of the basic splash of a mutual correlation function: peak amplitudes, gravity center of the area and gravity center of the energy. The outcomes of statistical data processing are reviewed at simulation source. Is showing, that the least error of a fix position of simulation source arises using the gravity center of energy.
1. Каллакот Р. Диагностика повреждений.-М.: Мир,1989.-512 с.
2. Баранов В.М. Акустические измерения в ядерной энергетике.-М.: Энергоатомиздат, 1990.-320 с.
3. Грешников В.А., Дробот Ю.Б. Акустическая эмиссия. Применение для испытаний материалов и изделий.-М.: Изд-во стандартов, 1976.-272 с.
4. Безпрозванный А.А., Владимирский А.А., Владимирский И.А., Ненюк А.Т. Повышение достоверности поиска утечек трубопроводов тепловых сетей// Энергетика и электрофикация.-№2 (199), 2000.-С.29-32.
5. Акусто-эмиссионая диагностика конструкций/ А.Н.Серьезнов, Л.Н.Степанова, В.В.Муравьев и др.-М.: Радио и связь, 2000.-280 с.
6. Бабак В.П., Хандецький В.С., Шрюфер Е. Обробка сигналів.-К: Либідь, 1999.-496 с.
7. Гулевский И.В. Применение методов неразрушающего контроля для оценки состояния конструкций планера //Труды ЦАГИ.-№ 2631, 1998.-С.178-181.
8. Кузнецов Н.С. К вопросу контроля механических свойств изделий из стали с помощью акустической эмиссии // Техническая диагностика и неразрушающий контроль.-№ 3, 1990.-С.65-71.
9. Владимирский А.А., Владимирский И.А. Оценка некоторых погрешностей корреляционного течеискателя// Зб.накових праць ІПМЕ НАНУ.-Вип.2, 1999.-С.118-126.
10. Владимирский А.А., Владимирский И.А. К формированию модели диагностируемого участка трубопроводной системы для решения задач течеискания // Зб.накових праць ІПМЕ НАНУ.-Вип.7, 2001.-С.66-69.
11. Владимирский А.А., Владимирский И.А., Семенюк Д.Н. Уточнение диагностической модели трубопровода для повышения достоверности течеискания //Акустичний вісник.-Т.8, № 3, 2005.-С.3-16.
12. Бать М.И., Джанелидзе Г.Ю., Кельзон А.С. Теоретическая механика в примерах и задачах. ТI-М.: Изд-во Наука, 1967.-512 с.
13. Горелик С.С., Расторгуев Л.Н., Скаков Ю.А. Рентгенографический и электронно-оптический анализ.-М.: Металлургия, 1970.-367 с.
14. Розенберг В.Я. Радиотехнические методы измерения параметров процессов и систем.-М.: Изд-во стандартов, 1970.-308 с.
15. Отнес Р., Энексон Л. Анализ временных рядов. Основные методы.-М.: Мир, 1982.-428 с.
Ответы на вопросы [_Задать вопроос_]
Читайте также
Информационно-измерительные системы
Ковальов О.І. Вимірювання у процесно-орієнтованих стандартахПолякова М.В., Ищенко А.В., Худайбердин Э.И. Порогово-пространственная сегментация цветных текстурированных изображений на основе метода JSEG
Дзюбаненко А. В. Организация компьютерных систем для анализа изображений
Гордеев Б.Н., Зивенко А.В., Наконечный А.Г. Формирование зондирующих импульсов для полиметрических измерительных систем
Богданов А.В., Бень А.П., Хойна С.И. Релаксация обратного тока диодов Шоттки после их магнитно-импульсной обработки (МИО)
Тверезовский В.С., Бараненко Р.В. Проектирование измерителя добротности варикапов
Тверезовский В.С., Бараненко Р.В. Оптимизированная модель измерителя доб-ротности варикапов
Руднєва М.С., Кочеткова О.В., Задорожній Р.О. Принципи побудови оптимальної структури інформаційно-вимірювальної системи геометричних розмірів об’єктів в діапазоні від 1 нм до 1000 нм
Биленко М.С., Рожков С.А., Единович М.Б. Идентификация деформаций пе-риодических структур с использованием систем технического зрения
Рашкевич Ю.М., Ковальчук А.М., Пелешко Д.Д. Афінні перетворення в модифікаціях алгоритму RSA шифрування зображень
Дидык А.А., Фефелов А.А, Литвиненко В.И., Шкурдода С.В., Синяков Ф. В. Классификация масс-спектров с помощью кооперативного иммунного алгоритма
Клименко А.K. Обратная модель для решения задач в системах с многосвязными динамическими объектами
Завгородній А.Б. Порівняльне дослідження твердотільних і рідиннофазних об'єктів методом газорозрядної візуалізації
Голощапов С.С., Петровский А.В., Рожко Ж.А., Боярчук А.И. Измерение доб-ротности колебательного контура на основе метода биения частот
Кириллов О.Л., Якимчук Г.С. Диагностирование критерия безопасности при заполнении замкнутых объемов СПЖ косвенным методом
Долина В.Г. Проблеми підвищення точності рефрактометра на основі прозорих порожнистих циліндрів.
Самков О.В., Захарченко Ю.А. Застосування алгоритму клонального відбору для побудови планів модернізації авіаційної техніки
Попов Д.В. Метод формування регламентів технічного обслуговування повітряних суден
Казак В.М., Чорний Г.П., Чорний Т.Г. Оцінювання готовності технічних об’єктів з урахуванням достовірності їх контролю
Тверезовский В.С., Бараненко Р.В. Технические аспекты проектирования цифрового измерителя добротности варикапов
Тверезовский В.С., Бараненко Р.В. Технические аспекты проектирования устройства для разбраковки варикапов по емкостным параметрaм и добротности
Сосюк А.В. Інтелектуальний автоматизований контроль знань в системах дистанційного навчання
Соколов А.Є. Деякі аспекти систезу комп’ютеризованої адаптивної системи навчання
Полякова М.В., Волкова Н.П., Іванова О.В. Сегментація зображень стохастичних текстур амплітудно-детекторним методом у просторі вейвлет-перетворення
Луцкий М.Г., Пономаренко А.В., Филоненко С.Ф. Обработка сигналов акустической эмиссии при определении положения сквозных дефектов
Литвиненко В.И., Дидык А.А., Захарченко Ю.А. Компьютерная система для решения задач классификации на основе модифицированных иммунных алгоритмов
Лубяный В.З., Голощапов С.С. Прямоотсчетные измерители расхождений емкостей
Беляев А.В. Построение навигации для иерархических структур в WEB-системах и системах управления WEB-сайтом
Терновая Т.И., Сумская О.П., Слободянюк И.И., Булка Т.И. Контроль качества тканей специального назначения с помощью автоматических систем.
Шеховцов А.В. Інформаційний аспект: розпізнавання образів індивідуума.
Полякова М.В. Определение границ сегмента упорядоченной текстуры на изображении с однородным фоном с помощью многоканального обнаружения пачки импульсов.
Литвиненко В.И. Прогнозирования нестационарных временных рядов с помощью синтезируемых нечетких нейронных сетей
Ковриго Ю.М., Мисак В.Ф., Мовчан А.П., Любицький С.В. Автоматизована система діагностики генераторів електростанцій
Браїловський В.В., Іванчук М.М., Ватаманюк П.П., Танасюк В.С. Керований детектор імпульсного ЯКР спектрометра
Забытовская О.И. Построение функции полезности по экспериментальным данным.
Шиманські З. Апаратні засоби сегментації мовного сигналу
Хобин В.А., Титлова О.А. К вопросу измерения парожидкостного фронта в дефлегматоре абсорбционно-диффузионной холодильной машины (АДХМ)
Фефелов А. А. Использование байесовских сетей для решения задачи поиска места и типа отказа сложной технической системы
Слань Ю. М., Трегуб В. Г. Оперативна нейромережна ідентифікація складних об’єктів керування
Ролик А.И. Модель управления перераспределением ресурсов информационно-телекоммуникационной системы при изменении значимости бизнес-процессов
Кириллов О.Л., Якимчук Г.С., Якимчук С.Г. Изучение электрического поля с помощью датчика измерителя электростатического потенциала на модели замкнутого металлического объема
Грицик В.В. Застосування штучних нейронних мереж при проектуванні комп’ютерного зору.
Гасанов А.С. Информационные технологии построения систем прогнозирования отказов
Шеховцов А.В., Везумский А.К., Середа Е.С. Алгоритм сжатия информации без потерь: модифицированный алгоритм LZ77
Ходаков В.Е., Жарикова М.В., Ляшенко Е.Н. Методы и алгоритмы визуализации пространственных данных на примере моделирования распространения лесных пожаров.
Полякова М.В., Крылов В.Н. Обобщённые масштабные функции с компактным носителем в задаче сегментации изображений упорядоченных текстур. – C. 75 – 84.
Полторак В.П., Дорогой Я.Ю. Система распознавания образов на базе нечеткого нейронного классификатора.
Литвиненко В.И. Синтез радиально-базисных сетей для решения задачи дистанционного определения концентрации хлорофилла.
Бражник Д.А. Управление совмещением изображения объекта в сцене и эталонного изображения.
Мороз В. В. R-D проблема и эффективность систем сжатия изображений.
Крылов В.Н., Полякова М.В., Волкова Н.П. Контурная сегментация в пространстве гиперболического вейвлет-преобразования с использованием математической морфологии.
Квасников В.П., Баранов А.Г. Анализ влияния дестабилизирующих факторов на работу биканальной координатно-измерительной машины.
Казак В.М., Гальченко С.М., Завгородній С.О. Аналіз можливості застосування імовірнісних методів розпізнавання для виявлення пошкоджень зовнішнього обводу літака.
Тищенко И.А., Лубяный В.З. Управление коммутационными процессами в интегрированных сетях связи.
Корниенко-Мифтахова И.К.,Филоненко С.Ф. Информационно-измерительная система для анализа характеристик динамического поведения конструкций.
Тверезовский В.С., Бараненко Р.В. Модель измерителя емкости с линейной шкалой измерений.
Полякова М.В., Крылов В.Н. Мультифрактальный метод автоматизированного распознавания помех на изображении.
Рожков С.О., Федотова О.М. Алгоритм розпізнавання дефектів тканин для автоматичної системи контролю якості.
Бражник Д.А. Использование проективного преобразования для автоматизации обнаружения объектов.
Ходаков В.Є., Шеховцов А.В., Бараненко Р.В. Математичні аспекти створення автоматизованої системи „Реєстр виборців України”