УДК 621.397

Практика использования автоматизированных систем обработки изображений показывает, что наиболее информативной частью изображений при распознавании являются контуры [1]. Переход к контурной обработке позволяет обеспечить инвариантность к трансформациям яркости и  на несколько порядков снизить объем обрабатываемой информации. В ряде работ показано, что для помехоустойчивого подчеркивания контуров целесообразно использовать преобразование  Гильберта (ПГ) [1]. Прямое (ПГ) и обратное (ОПГ) преобразований может быть представлено парой формул:

где         –  строка (столбец) изображения; х – пространственная координата.

ПГ трактуется также как свертка сигнала с гиперболой , т.е., где * - операция свертки.

            ПГ обладает целым рядом полезных, с точки зрения операции выделения контуров, свойств [1]:

– достаточно эффективно проводит операцию подчеркивания перепадов интенсивности;

– имеет высокую помехоустойчивость;

– линейно;

– имеет нулевое математическое ожидание;

– не изменяет дисперсию процесса;

– сближает по форме идеальный и протяженный перепады интенсивности.

Обычно полагают, что результат преобразования должен принимать конечные значения в каждой точке оси абсцисс. Однако, операция подчеркивания контуров выдвигает другие требования. Простое дифференцирование идеального перепада интенсивности приводит к d-функции. Поэтому возникает необходимость использовать понятие обобщенной функции. Формула (1) задает функционал на множестве пробных функций [2 ]. Непосредственно видно, что данный функционал линеен. Интеграл в правой части выражения (1) следует понимать формально-аксиоматически, а не как предел соответствующих интегральных сумм.

Обрабатываемое  изображение чаще всего является локально неоднородным. Процесс распознавания целесообразно проводить на разных уровнях детализации объекта в зависимости от поставленной задачи. Например, в ряде практически важных задач изображение можно распознать по внешнему контуру объекта (силуэту), в других информативной частью являются мелкие детали объекта. Таким образом,  при распознавании изображение целесообразно подвергнуть преобразованию, обладающему свойством пространственно- частотной локализации. Такими свойствами обладает вэйвлет-преобразование.

В данном разделе решается задача конструирования гиперболического вэйвлета, позволяющего объединить достоинства ПГ с пространственно- частотной локализацией распознаваемого изображения. При этом конструирование базиса следует проводить в пространстве обобщенных функций.

ПГ является сверткой входного сигнала с гиперболой. Гипербола является сингулярной функцией с разрывом первого рода в точке . Поэтому конструирование базиса непрерывных вэйвлет- функций, следует производить в функциональном пространстве обобщенных функций. В качестве базисных функций вэйвлет- преобразования будут использоваться гиперболические функции различного масштаба , где a - масштабный коэффициент. Такое преобразование назовем гиперболическим вэйвлет преобразованием (ГВП). ПГ является частным случаем ГВП с масштабным коэффициентом, равным 1. ГВП можно сконструировать без учета сингулярности и в точке  импульсной характеристике присвоить значение 0. Такое преобразование будем называть в дальнейшем фовеальным ГВП (ФГВП). Можно также  аппроксимировать разрыв какой- либо конечной величиной G. Выбор величины G будет обсужден ниже.

В случае ФГВП анализ производится в функциональном пространстве L²(R). В противном случае конструирование будет производиться с учетом сингулярности в пространстве обобщенных функций.

Для анализа свойств ФГВП в пространстве дискретных функций рассмотрим  функциональное пространство L²(R) функций S(x), определенное на всей действительной оси и обладающей конечной энергией (нормой):

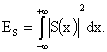
Сконструируем базис этого пространства. Базисные функции для обеспечения пространственной локализации должны стремиться к нулю на ± µ.  Для того, чтобы покрыть пространство R(- µ,+ µ) с помощью локализованных базисных функций, необходимо предусмотреть систему сдвигов. Для обеспечения частотной локализации применяются масштабные преобразования. Сконструируем базис функционального пространства  L²(R) с помощью непрерывных масштабных преобразований и сдвигов вэйвлета y(х) [3]:

где а – масштабный коэффициент, b – параметр сдвига, . Эти функции назовем гиперболическим вэйвлет- преобразованием (ГВП).

В качестве материнского вэйвлета ФВГП будем рассматривать следующую функцию:

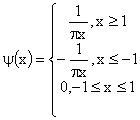
Рассмотрим свойства материнского вэйвлета . Норма функции определяется выражением:

.

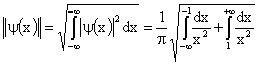В отличие от непрерывного ГВП, в котором несобственный интеграл понимается формально- аксиоматически, в данном случае несобственный интеграл может пониматься в смысле главного значения. Далее будет показано, что функции, образованные из материнского вэйвлета путем масштабных преобразований и сдвигов образуют базис Рисса и имеют ту же норму.

Необходимым условием для построения безусловно устойчивого базиса является условие осцилляций или знакопеременности.

.

Гиперболические функции являются нечетными, поэтому условие осцилляций выполняется. Более того, функция, обратная гиперболе, также является гиперболой. Поэтому условие осцилляций выполняется и при интегрировании по Лебегу.

Гиперболический вэйвлет быстро спадает и, следовательно, обеспечивает хорошую локализацию в пространстве. Оценка хорошей локализации

где n принадлежит множеству положительных целых чисел.

Для гиперболического вэйвлета оно выполняется при :

.

Обратным является базис  . С помощью него можно построить реконструкционную формулу:

.

Обратный (парный) базис также является вэйвлетом.

Все нечеткие начальные моменты гиперболического вэйвлета равны 0.

.

Это свойство нечетной функции. Обладающий большим числом нулевых моментов гиперболический вэйвлет позволяет, игнорируя наиболее регулярные полиномиальные составляющие сигнала, анализировать мелкомасштабные флуктуации и особенно высокого порядка.

Основные положения этой работы проверялись на тестовом изображении, представленном на рис.1a . Обработка проводилась с помощью гиперброического преобразования разного масштаба. На рис.1б представлено сечение тестового изображения, обработанное с помощью гиперболической маски масштаба a=1. Малые по размеру детали изображения с высокой контрастностью имеют в области перепада интенсивности самый высокий пик. При увеличении масштаба гиперболы размеры этого пика уменьшаются (рис.1.в).В тоже время увеличивается амплитуда пика на границах крупномасштабных деталей объекта. Таким образом, изменяя масштаб гиперболы можно регулировать детальность изображения объекта.

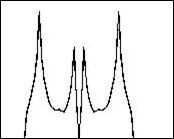
а)                                                          б)                                            в)

Рис. 1 Результаты экспериментов

а) – тестовое изображение,

б) и в) – строка изображение в области гиперболического вейвлет-преобразования на разных масштабах.

1.    Крылов В.Н., Максимов М.В. Вторичные преобразователи сигналов изображений. – Одесса, Астропринт, 1997

2.    Баскаков С.И. Радиотехнические цепи и сигналы.–М. Высш. шк., 1988. – 448 с.

3.    Дремин И.М.,. Иванов О.В, Ничайло В.А.. Вейвлеты и их использование // Успехи физических наук. Т. 171, №5. С. 465-501