УДК 519.8:004.032.26
ПОБУДОВА ГІБРИДНИХ МОДЕЛЕЙ НА ОСНОВІ ПРИХОВАНИХ МАРКІВСЬКИХ МОДЕЛЕЙ ТА НЕЙРОННИХ МЕРЕЖ
Степанкова Г.А., Баклан І.В.
Існування двох підходів:
· приховані марківські моделі (ПММ) (Hidden Markov Model (HMM)),
· штучні нейронні мережі (ШНМ),
взаємно доповнюючих і компенсуючих властиві їм недоліки, призводить до ідеї комбінувати ці структури в рамках однієї нової моделі, яку можна визначити як гібридну ПММ/ШНМ модель. У 90-х рр. були спроби досліджувати такі моделі [1, 2, 3, 4, 5, 6]. Гібридна модель дозволяє ефективно об'єднати переваги марківських моделей та нейронних мереж, тобто ПММ забезпечує можливість моделювання довготривалих залежностей, а ШНМ забезпечує непараметричну універсальну апроксимацію, оцінку вірогідності, алгоритми дискриминантного навчання, зменшення числа параметрів для оцінки, які зазвичай потрібні для стандартних ПММ. Результатом використання таких гібридних структур з'явилося значне підвищення якості розпізнавання в порівнянні із стандартними методами.
Опис гібридної моделі багатошарового персептрону і ПММ
При використанні ПММ у формулі (1)
![]() , (1)
, (1)
де ![]() є вірогідністю того, що часткова послідовність спостережень
є вірогідністю того, що часткова послідовність спостережень ![]() була породжена моделлю, а у момент часу
була породжена моделлю, а у момент часу ![]() спостерігався стан
спостерігався стан ![]() і був згенерований вектор спостережень
і був згенерований вектор спостережень![]() , необхідно мати оцінку емісійної вірогідності
, необхідно мати оцінку емісійної вірогідності ![]() , яка є вірогідністю спостереження вектора, при заданому гіпотетичному ПММ стані
, яка є вірогідністю спостереження вектора, при заданому гіпотетичному ПММ стані ![]() . На початку 90-х рр. Боурлард та ін. [7, 8, 1, 5] запропонували використовувати багатошаровий персептрон (БП) для оцінки вірогідності, яка є апостеріорною вірогідністю ПММ стані
. На початку 90-х рр. Боурлард та ін. [7, 8, 1, 5] запропонували використовувати багатошаровий персептрон (БП) для оцінки вірогідності, яка є апостеріорною вірогідністю ПММ стані ![]() . при заданому спостережуваному векторі
. при заданому спостережуваному векторі ![]() . Цю вірогідність відповідно до правила Байеса, можна перерахувати в емісійну вірогідність.
. Цю вірогідність відповідно до правила Байеса, можна перерахувати в емісійну вірогідність.
Формально це виглядає таким чином. Хай ![]() при
при ![]() – вихідне значення k-го нейрона вихідного шару персептрона, тоді
– вихідне значення k-го нейрона вихідного шару персептрона, тоді ![]() можна пов'язати з дискретним ПММ станом
можна пов'язати з дискретним ПММ станом ![]() . Тепер, якщо об'єднати множину параметрів
. Тепер, якщо об'єднати множину параметрів ![]() , визначену для ПММ з множиною параметрів БП
, визначену для ПММ з множиною параметрів БП ![]() , і використовувати для навчання послідовність векторів, розмічену в термінах станів, тобто у момент часу n вхідним вектором для БП є вектор
, і використовувати для навчання послідовність векторів, розмічену в термінах станів, тобто у момент часу n вхідним вектором для БП є вектор ![]() з міткою
з міткою ![]() . Тоді можна показати [7, 9, 10], що якщо:
. Тоді можна показати [7, 9, 10], що якщо:
· БП містить достатня кількість прихованих нейронів, щоб апроксимувати функцію відображення вхідного вектора у вихідний
· БП не “переучений” (“перенавчання” виражається в дуже детальній адаптації вагів до неістотних флуктуацій або нерегулярностям навчальних даних, що приводить до значних погрішностей при розпізнаванні)
· БП не знаходиться в локальному мінімумі, після процедури навчання,
то оптимальне значення виходу БП є розподілом вірогідності по дискретних ПММ станах, яке обумовлене вхідним вектором
![]() (2)
(2)
де ![]() – множина параметрів, отримана при навчанні БП (Multilayer Perceptron (MLP)).
– множина параметрів, отримана при навчанні БП (Multilayer Perceptron (MLP)).
Крім того, в [7] було описано просте розширення запропонованої моделі з метою використання контекстної інформації, тобто як вхід для персептрона використовувати послідовність з 2c + 1 векторів ![]() . Тоді (2) можна переписати
. Тоді (2) можна переписати
![]() (3)
(3)
Таке удосконалення дає можливість враховувати кореляцію векторів, що дозволяє подолати обмеження, пов'язані із статистичною незалежністю векторів спостережень.
Крім того, в [7] запропоновано використовувати як вхідний параметр ПММ стан, обчислений на попередньому тимчасовому кроці:
![]() (4)
(4)
Таким чином, в цій моделі використовується нейронна мережа із затримкою часу (Time-Delay Neural Network (TDNN)), і структура такої системи представлена на мал. 1.
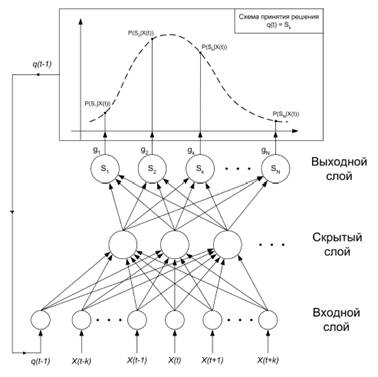
Мал. 1 Оцінка вірогідності за допомогою TDNN мережі
Запропонована обчислювальна структура працює таким чином. У кожен момент часу n на вхідний шар БП подається послідовність векторів ![]() і ПММ перебування на попередньому часовому кроці, при цьому на вихідному шарі формуватиметься розподіл вірогідності по поточному стану ПММ, обумовлене
і ПММ перебування на попередньому часовому кроці, при цьому на вихідному шарі формуватиметься розподіл вірогідності по поточному стану ПММ, обумовлене ![]() і
і ![]() .
.
Оскільки вихідний вектор БП є апроксимацією апостеріорної вірогідності, то ![]() , є оцінкою
, є оцінкою
![]() , (5)
, (5)
яка неявно включає емісійну вірогідність ![]() і апріорну вірогідність ПММ стану
і апріорну вірогідність ПММ стану ![]() . Оскільки вірогідність в (5) бере участь як мультиплікативний член, то це дає можливість змінювати апріорну вірогідність стану під час класифікації без перенавчання персептрона, нормувати вихідну вірогідність персептрона залежно від використовуваного повчального корпусу даних. І тоді, щоб правдоподібність
. Оскільки вірогідність в (5) бере участь як мультиплікативний член, то це дає можливість змінювати апріорну вірогідність стану під час класифікації без перенавчання персептрона, нормувати вихідну вірогідність персептрона залежно від використовуваного повчального корпусу даних. І тоді, щоб правдоподібність ![]() можна було використовувати як емісійну вірогідність для ПММ, необхідно вихід персептрона
можна було використовувати як емісійну вірогідність для ПММ, необхідно вихід персептрона ![]() поділити на відносну частоту зустрічей стану
поділити на відносну частоту зустрічей стану ![]() в навчальній вибірці, що в результаті дає нам оцінку виразу
в навчальній вибірці, що в результаті дає нам оцінку виразу
![]() (6)
(6)
При розпізнаванні масштабуючий член ![]() залишається постійним для всіх станів і не впливає на класифікацію.
залишається постійним для всіх станів і не впливає на класифікацію.
Опис гібридної моделі рекурентної мережі і ПММ.
Аналогічна модель була запропонована Робінсоном і ін. [11, 12, 13, 14], які використовували рекурентну мережу замість TDNN мережі, також для оцінки емісійної вірогідності ПММ.
Автори запропонували в основних рівняннях для лінійних динамічних систем замінити лінійні матричні оператори на нелінійну мережу із зворотними зв'язками, і в результаті була отримана обчислювальна структура, приведена на малюнку 2. Поточний вектор ![]() поступає на вхід мережі спільно з поточним вектором стану
поступає на вхід мережі спільно з поточним вектором стану ![]() . Ці вектори проходять через стандартну мережу без зворотних зв'язків, щоб отримати вихідний вектор
. Ці вектори проходять через стандартну мережу без зворотних зв'язків, щоб отримати вихідний вектор ![]() і наступний вектор стану
і наступний вектор стану ![]() . Якщо визначити комбінований вхідний вектор як
. Якщо визначити комбінований вхідний вектор як ![]() , а матрицю вагів зв'язків мережі як W і V, тоді
, а матрицю вагів зв'язків мережі як W і V, тоді
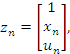 (7)
(7)
![]() , (8)
, (8)
![]() , (9)
, (9)
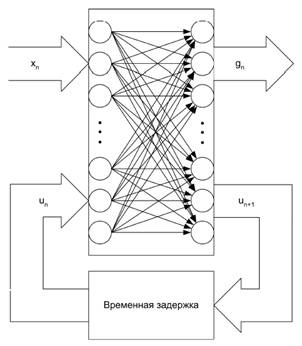
Мал. 2. Рекурентна нейронна мережа
Включення 1 в (7) дає можливість створити зсув для забезпечення нелінійності. Аналогічно моделі Боурларда з використанням TDNN мережі вихід рекурентної мережі є оцінкою апостеріорної вірогідності ПММ стану ![]() у момент часу n:
у момент часу n:
![]() (10)
(10)
Теоретичні підстави для такої інтерпретації приведені в роботі [15].
При використанні рекурентної мережі для оцінки емісійної вірогідності в гібридній моделі можна отримати досить великий контекст, за рахунок використання вектора внутрішнього стану ![]() .
.
При використанні ПММ робляться припущення про те, що спостереження статистично незалежні і марківський процес першого порядку, тобто
![]() (11)
(11)
де – послідовність ПММ станів в моменти часу ![]() . Використання рекурентної мережі дозволяє скоротити число припущень, тобто
. Використання рекурентної мережі дозволяє скоротити число припущень, тобто
![]() (12)
(12)
що дозволяє враховувати контекст для локальної моделі спостережень. Тоді отримаємо
![]() (13)
(13)
Оскільки співмножник ![]() не залежить від послідовності фонів, то на етапі розпізнавання його можна ігнорувати. Оскільки рекурентна мережа використовується для оцінки
не залежить від послідовності фонів, то на етапі розпізнавання його можна ігнорувати. Оскільки рекурентна мережа використовується для оцінки ![]() , то необхідно обчислити член
, то необхідно обчислити член ![]() , що залишився. Один з простих способів обчислення – це припустити, що поточний стан не залежить від спостережуваного контексту [16], тобто
, що залишився. Один з простих способів обчислення – це припустити, що поточний стан не залежить від спостережуваного контексту [16], тобто
![]() (14)
(14)
де ![]() можна визначити як відносну частоту зустрічей стану
можна визначити як відносну частоту зустрічей стану ![]() в навчальній вибірці, тобто отримуємо результат аналогічний моделі Боурларда.
в навчальній вибірці, тобто отримуємо результат аналогічний моделі Боурларда.
Навчання гібридної моделі
Навчання гібридної моделі полягає в оцінці параметрів як марківського ланцюга, так і вагів нейронної мережі. Поки не існує алгоритму, який би дозволив одночасно оцінити обидві множини параметрів і для ПММ, і для нейронної мережі. Крім того, оскільки для нейронної мережі використовується навчання “з вчителем”, то потрібен значний об'єм даних, розмічених вручну.
Боурлард запропонував ітераційну процедуру навчання, яка стартує з початкової розмітки навчальних даних. На цих даних відбувається навчання мережі. Далі спільно, використовуючи навчену мережу для оцінки емісійної вірогідності і алгоритм Вітербі, відбувається переразмітка навчальних даних. На отриманій розмітці знову відбувається навчання мережі і ітерація повторюється. Початкова сегментація може бути отримана за допомогою стандартної ПММ або просто діленням послідовності спостережень на рівні сегменти, причому кожен сегмент повинен бути помічений відповідним ПММ станом. Аналогічний метод був запропонований в [2].
При використанні гібридних моделей з рекурентними мережами T. Робінсон [16] запропонував варіант навчання з використанням алгоритму Вітербі для оцінки параметрів системи, який викладений нижче.
Параметри системи модифікуються, використовуючи алгоритм Вітербі для максимізації логарифма правдоподібності найбільш вірогідної послідовності станів для навчальних даних. Перший прохід алгоритму Вітербі робиться, щоб розмітити послідовність векторів параметрів в термінах ПММ станів. Потім параметри системи підстроюються, щоб збільшити правдоподібність послідовності векторів параметрів. Ця максимізація відбувається в два етапи:
1. максимізація емісійної вірогідності,
2. максимізація транзитивної вірогідності.
Емісійна вірогідність максимізується, використовуючи метод градієнтного спуску, а транзитивна вірогідність – переоцінкою моделей тривалості. Таким чином, навчальний цикл складається з наступних кроків:
Крок 1. Розстановка міток фонів на кожен фрейм навчальних даних. Ця початкова розмітка зазвичай виконується експертом вручну.
Крок 2. На основі ручної розмітки будується модель тривалості фонів і обчислюється апріорна вірогідність фону, яка використовується для перетворення виходу рекурентної мережі в оцінку правдоподібності.
Крок 3. Аналогічно на основі ручної розмітки проводиться навчання рекурентної мережі.
Крок 4. Використовуючи параметри, обчислені на кроці 2, і рекурентну мережу, навчену на кроці 3, виконується розмітка додаткових навчальних даних і перехід до кроку 2.
У експериментах [16] було встановлено, що для навчання досить чотирьох ітерацій.
Тестування гібридних моделей
Гібридні моделі використовувалися в досить великому числі систем. І показали добрі результати. Боурлард і колеги в період 1988-1994 рр. провели цілий ряд успішних експериментів по застосуванню гібридної моделі в системах розпізнавання мови [7]. Так, наприклад, в систему розпізнавання злитої мови DECIPHER [17], яка використовувалася для завдання управління ресурсами проекту DARPA. Система DECIPHER була дикторо-залежною системою розпізнавання злитої мови побудовану на прихованих марківських моделях. Розмір словника складав 998 слів, з використанням моделі мови для пар слів, перплексия дорівнювала 60, а без моделі мови – дорівнювала 998. Крім того, використовувалася множина імовірнісних вимовних транскрипцій для слів, фонологічне і акустичне моделювання кросс-слов, контекстні залежні моделі фонів з множиною щільності.
У системі DECIPHER були використані як контекстнонезависимые, так і контексто-залежні моделі. У першому випадку багатошаровий персептрон був інтегрований в контекстну незалежну модель. Базова система мала 69 моделей фонів з одним розподілом емісійної вірогідності, кожне слово мало одну вимовну транскриприцию. Моделі фонів були ПММ, що складається з двох або трьох станів з параметричним скріпленням щільності вірогідності. Цей гібрид порівнювався із ПММ системою DECIPHER, в якій емісійна вірогідність моделювалася Гауссовимі сумішами. При цьому DECIPHER використовувався як стартова система для отримання початкової фонетичної розмітки на першій ітерації навчання багатошарового персептрона. В результаті експериментів було отримано значне поліпшення якості розпізнавання в порівнянні з контекстонезависимой системою, заснованою на ПММ.
Аналогічні експерименти були проведені Робінсоном, що використав гібрид ПММ і рекурентній мережі в системі розпізнавання злитої мови ABBOT (Cu-Con), яка була успішно протестована в рамках проекту November 1993 ARPA Wall Street Journal Test, а також в європейському проекті SQALE (Speech Quality Assessment for Linguistic Engineering) [19]. SQALE був присвячений порівнянню декількох провідних світових систем розпізнавання, таких як Cu-Con і CU-HTK, створені в Cambridge University Engineering Department (Великобританія), LIMSI з Laboratoire d’Informatique pour la Mecanique et les Sciences de l’Ingenieur (Франція) і PHILIPS the Man-MachineInterface group with Philips Research Laboratories (Німеччина). Системи CU-HTK, LIMSI і PHILIPS побудовані на базі ПММ і використовують для моделювання безперервну щільність.
Хеннеберг і колеги [22] запропонували ускладнення теоретичних основ, сформульованих Боурлардом і Морганом шляхом узагальнення локальної апостеріорної вірогідності на глобальну апостеріорну вірогідність моделі, сформульовану як новий навчальний алгоритм для гібридної моделі. Це розширення базується на роботі Франко і колег [23], в якій незалежна ПММ була замінена на модель, що дозволяє інтегрувати в себе акустичний контекст.
Висновок
Описана гібридна модель знайшла застосування в багатьох системах розпізнавання злитої мови з великими словниками, але не було спроб використовувати цей метод для задачі прогнозування на фінансово-економічних часових рядах. Описана гібридна модель продемонструвала дуже непогані результати в порівнянні з системами, побудованими на основі кожної з моделей, які складають гібрид, окремо. Дослідження показали, що не дивлячись на відносну простоту структури модель володіє цілим рядом потенційних переваг (в порівнянні із стандартними ПММ), які були підтверджені на практиці:
· Точність моделі – оцінка вірогідності за допомогою нейронної мережі не вимагає детальних припущень про форму статистичних розподілів, які повинні бути промодельовані. В результаті можна отримати точніші моделі.
· Дискримінантна здатність: за допомогою нейронної мережі значно простіше реалізувати дискримінантне навчання.
· Врахування контексту – оскільки описані моделі нейронних мереж можуть використовувати контекст, то локальна кореляція векторів може бути врахована при обчисленні розподілів вірогідності. З різних причин щось подібне важко реалізувати в стандартних ПММ.
· Економне використання параметрів (зниження розмірності системи) – оскільки всі розподіли вірогідності представлені тією ж множиною параметрів, що розділяються. Добре відомо, що “економічніше” моделювати межі між класами, чим поверхні функцій щільності (тобто правдоподібностей).
· Гнучкість – використання нейронних мереж для оцінювання акустичної вірогідності дозволяє легко поєднувати різноманітні параметри, наприклад такі, як суміш безперервних і дискретних вимірювань.
· Комплементарність – в деяких системах нейронна мережа забезпечує додатковою інформацією базову ПММ систему. Так, наприклад, в одному з експериментів комбінація ПММ з нейронною мережею (названою, “сегментною нейронною мережею”) дозволила значно підвищити якість розпізнавання [24, 25].
Проте не дивлячись на досягнуті успіхи, необхідно продовжувати дослідницькі роботи, направлені на розробку гібридних структур, що дозволяють проводити глобальне дискримінатне навчання, тобто на розробку моделей, заснованих на одночасному оцінюванні обох множин параметрів як ПММ, так і нейронної мережі при використанні одного критерію оптимізації. Крім того, поки залишаються відкритими питання, пов'язані з адаптацією таких систем, також необхідно підвищувати стійкість.
Reviewed existing hybrid models: hidden Markov models and neural networks. Examined principles of combining neural networks with hidden Markov models. Provided brief comparison of systems that use such architecture.
1. Bourlard H., Wellekens C. Links Between Markov Models and Multilayer Perceptrons // IEEE Transactions on Pattern Analysis and Machine Intelligence. 1990. Vol. 12. No. 12. pp. 1167-1178.
2. Franzini M.A., Lee K.F., Waibel A. Connectionist Viterbi training: а new hybrid method for continuous speech recognition // IEEE ICASSP 1990, pp. 425-428.
3. Haffner P., Franzini M.A., Waibel A. Integrating time alignment and neural networks for high performance continuous speech recognition // IEEE ICASSP 1991. pp. 105-108
4. Levin E. Word recognition using hidden control neural architecture // IEEE ICASSP 1990.
5. Morgan N., Bourlard H. Continuous speech recognition using multilayer perceptrons with hidden Markov models // ICCASP 1990, pp. 413-416
6. Niles L.T., Silverman H.F. Combining hidden Markov models and neural networks classi;ers // IEEE ICASSP 1990. pp. 417- 420.
7. Bourlard H., Morgan N. Connectionist Speech Recognition. A Hybrid Approach // The Kluwer International Series in Engineering and Computer Science, Vol. 247, Kluwer Academic Publishers, Boston, 1994.
8. Bourlard H., Morgan N. Continuous speech recognition by connectionist statistical methods // IEEE Transaction on Neural Networks. 1993. Vol. 4. No. 6. pp. 893-909.
9. Gish H. A probabilistic approach to the understanding and training of neural network classi`ers // IEEE ICASSP 1990. pp. 1361-1364.
10.Richard M.D., Lippmann R.P. Neural network classi`ers estimate Bayesian а posteriori probabilities // Neural Computation, 1991. No. 3. pp. 461-483.
11.Hochberg M. M., Renals S. J., Robinson A. J., Kershaw D. J. Large vocabulary continuous speech recognition using а hybrid connectionist-HMM system // Proceedings of CSLP, Yokohama, 1994. pp. 1499-1502.
12.Hochberg M. M., Renals S. J., Robinson A. J., Cook G. D. Recent improvements to the ABBOT large vocabulary csr system // IEEE ICASSP, Detroit, 1995. pp. 62-72.
13.Robinson A.J., Fallside F. Static and dynamic error propagation network with application to speech coding // In: D.Z. Anderson (Ed.), Neural Information Processing System, American Institute of Physics, New York, Denver, CO, 1988, pp. 635-641.
14.Robinson T. An application of recurrent nets to phone probability estimation // IEEE Transaction on Neural Networks, 1994. Vol. 5. No. 2. pp. 298-305.
15.McCullagh P., Nelder J. A. Generalized Linear Models // London: Chapman and Hall, 1983.
16.Robinson T., Hochberg M., Renals S. The use of recurrent neural networks in continuous speech recognition // In: C.H. Lee, F.K. Soong, K.K. Paliwal (Eds), Automatic Speech and Speaker Recognition: Advanced Topics, The Kluwer International Series in Engineering and Computer Science, Kluwer Academic Publishers, Boston, USA 1996.
17.Cohen M., Murveit H., Bernstein H., Price P., Weintraub M. The DECIPHER speech recognition system // IEEE ICASSP, Albuquerque, 1990. pp. 77-80.
18.Morgan N., Bourlard H. Hybrid neural network/ hidden Markov model system for continuous speech recognition // Intl. Journal of Pattern Recognition and Ariacial Intelligence, Special Issue on Advances in Pattern Recognition Systems using Neural Networks (I. Guyon and P. Wang, Eds.). 1993. Vol. 7, No. 4.
19.Young S.J., Adda-Dekker M., Aubert X. Multilingual large vocabulary speech recognition: the European SQALE project // Computer Speech and Language, 1997, 11, pp. 73-89.
20.Hochberg M., Renals S. & Robinson A. ABBOT: the CUED hybrid connectionist-HMM large vocabulary recognition system // Proceedings of the Spoken Language Technology Workshop, 1995. pp.170-178, Austin, TX, U.S.A.
21.Kershaw D. J., Hochberg M. M., Robinson A. J. Context dependent classes in а hybrid recurrent network-HMM speech recognition system // Cambridge University Engineering Department, Technical Report, CUED/F- INFENG/TR.217.1995.
22.Henneberg J., Ris C., Bourlard H., Renals S., Morgan N. Estimation of global posteriors and forward-backward training of hybrid HMM/ANN systems // Proceedings of EUROSPEECH, 1997. Vol. 4, Rhodi, pp. 1951-1954.
23.Franco H., Cohen M., Morgan N., Rumelhart D., Abrash V. Context-dependent connectionist probability estimation in а hybrid hidden Markov model-neural net speech recognition system // Computer Speech and Language. 1994. 8. pp. 211 - 222.
24.Austin S., Zavaliagkos G., Makhoul J., Schwartz R. Speech recognition using segmental neural nets // IEEE ICASSP, San Francisco, March 1992, pp. I-625-628.
25.Austin S., Zavaliagkos G., Makhoul J., Schwartz R. Improving state-of the-art continuous speech recognition system using the N-best paradigm with neural networks // Proceedings DARPA Speech and Natural Language Workshop, Harriman, NY (Morgan Kaufmann, Los Altos, CA). 1992. pp. 180-184.
Ответы на вопросы [_Задать вопроос_]
Читайте также
Моделирование объектов и систем управления
Соколов А.Е., Махова Е.О. Моделирование процесса принятия педагогического решения при компьютеризированном обученииСлавко О.Г. Порівняльний аналіз керування регулятором на основі локальної моделі керованого процесу та П-регулятором
Войтенко В.В., Дикусар Е.В, Ситников В.С. Определение частоты среза устройства сглаживания данных на основе метода скользящего среднего
Передерій В.І. Алгоритм визначення та оцінки характеристик ефективності комп’ютерних систем на початковій стадії проектування в умовах невизначенності
Ляшенко С.А, Ляшенко А.С. Оценка модели псевдолинейной регрессии
Ладієва Л.Р. Математична модель процесу газової мембранної дистиляції
Носов П.С., Косенко Ю.І. Нечіткі моделі і методи ідентифікації та прогнозу стану інформаційної моделі студента
Китаев А.В., Глухова В.И. Анализ работы синхронного двигателя с неявнополюсным ротором по данным каталога
Дорошкевич В.К., Пироженко А.В., Хитько А.В., Хорольский П.Г. К определению требований к системам увода космических объектов
Голінко І.М., Ковриго Ю.М., Кубрак А.І. Настройка системи керування за імпульсною характеристикою об’єкта
Яшина К.В., Садовой А.В. Комплексная математическая модель тепловых процессов, происходящих в дуговых электросталеплавильных печах
Шейник С.П., Рудакова А.В. Использование функций принадлежности для моделирования параметров распределенных объектов
Хомченко А.Н., Литвиненко Е.И. Метод барицентрического усреднения граничных потенциалов электростатического поля
Селяков Е. Б. Моделирование требований к техническим системам методами математической логики
Тодорцев Ю.К., Ларіонова О.С., Бундюк А.М. Математична модель контура теплопостачання когенераційної енергетичної установки
Кириллов О.Л. , Якимчук Г.С. Моделирование процесса управления системой перегрузки углеводородных жидких топлив
Шеховцов А.Н., Козел В.Н. Построение математической модели формирования распределенных систем
Китаев А.В., Глухова В.И. Анализ поведения генератора постоянного тока по данным каталога
Хомченко А.Н., Козуб Н.О. Задачі наближення функцій: від лагранжевих до серендипових поліномів
Хобин В.А., Титлова О.А. Определение температуры парожидкостной смеси в дефлегматоре АДХМ по результатам измерений температуры его поверхности
Григорова Т.М., Усов А.В. Вероятностно-статистическое моделирование маршрутизированных пассажиропотоков в крупных городах
Горач О.О., Тернова Т.І. Моделювання технологічного процесу одержання трести при використані штучного зволоження з урахуванням складу мікрофлори
Дубік Р.М., Ладієва Л.Р. Математична модель розділення неоднорідних рідких систем
Казак В.М, Лейва Каналес Родриго, Яковицкая Е.Ю. Моделирование динамики полета магистрального самолета на исследовательском стенде
Завальнюк И.П. Исследование процесса торможения автомобиля как критического режима динамической системы
Дмитриев С.А., Попов А.В. Построение портрета неисправностей проточной части газотурбинного двигателя на примере АИ-25
Русанов С.А., Луняка К.В., Клюєв О.І., Глухов Г.М. Математичне моделювання робочого процесу в апаратах з віброкиплячим шаром та розробка систем автоматизованого моделювання гідродинаміки віброкиплячих шарів
Боярчук В.П., Сыс В.Б. Экспериментальные исследования влияния технологии шлихтования на изменение жесткости текстильных нитей
Селін Ю.М. Використовування контекстних марківських моделей для аналізу дії промислових вибухів на будівельні конструкції
Рудакова А.В. Проблемы интеграции сложных систем
Передерій В.І., Касап А.М. Математична модель та алгоритм автоматизації розрахунку параметрів комп’ютеризованих систем працюючих у реальному часі
Передерий В.И., Еременко А.П. Математические модели и алгоритмы принятия релевантных решений пользователями автоматизированных систем с учетом личностных и внешних факторов на базе генетических алгоритмов
Михайловская Т.В., Михалев А.И., Гуда А.И. Исследование правил клеточных автоматов для моделирования процессов затвердевания квазиравновесных бинарных сплавов
Хомченко А.Н., Колесникова Н.В. Явление «сверхсходимости» в задаче Прандтля для уравнения Пуассона
Китаев А.В., Глухова В.И. Анализ работы трансформатора по данным каталога
Квасницкий В.В., Ермолаев Г.В., Матвиенко М. В., Бугаенко Б.В., Квасницкий В.Ф. Оценка применимости метода компьютерного моделирования к исследованию напряженно-деформиррованного состояния цилиндрических узлов
Китаев А.И., Глухова В.И. Анализ работы асинхронного двигателя по данным каталога
Шелестов А.Ю Имитационная модель взаимодействия GRID-узлов с очередью доступа к общей памяти
Chizhenkova R.A. Mathematical Aspects of Bibliometrical Analysis of Neurophysiological Investigations of Action of Non-ionized Radiation (Medline-Internet)
Хомченко А.Н., Козуб Н.А. Геометрическое моделирование дискретных элементов с криволинейными границами
Славич В.П. Модель автоматизованої системи управління потоками транспортних засобів
Маркута О.В., Мысак В.Ф. Программная реализация и исследование особенностей метода группового учета аргументов
Бакшанська Т.Д., Рижиков Ю.Г., Тодорцев Ю.К. Математична модель процесу горіння природного газу з рециркуляцією продуктів згорання для цілей управління
Хомченко А.Н. Новые решения обобщенной задачи Бюффона
Передерий В.И., Еременко А.П. Математические модели и алгоритмы определения релевантности принимаемых решений с учетом психофункциональных характеристик пользователей при управлении автоматизированными динамическими системами
Ложечников В.Ф., Михайленко В.С., Максименко И.Н. Аналитическая много режимная математическая модель динамики газовоздушного тракта барабанного котла средней мощности
Ковриго Ю.М., Фоменко Б.В., Полищук И.А. Математическое моделирование систем автоматического регулирования с учетом ограничений на управление в пакете Matlab
Исаев Е.А., Наговский Д.А. Математическое описание влияния кривизны контактирующих тел на угол смачивания жидкости в межчастичном пространстве
Бідюк П.І., Литвиненко В.І., Кроптя А.В. Аналіз ефективності функціонування мережі Байєса
Тищенко И.А., Лубяный В.З. Математическое моделирование вокодера для определения оптимальной формы импульса сигнала возбуждения.
Николаенко Ю.И., Моисеенко С.В. Моделирование гармонического полиномиального базиса гексагона.
Козуб Н.А., Манойленко Е.С., Хомченко А.Н. Температурный тест для модифицированных базисов бикубической интерполяции.
Клименко А.К. Об упрощенном численном конструировании обратной модели динамического объекта.
Китаев А.В., Сушич Е.Ф. Расчет погрешностей измерительных трансформаторов.
Передерій В.І.,Касап А.М. Математична модель та алгоритм автоматизації розрахунку параметрів комп’ютеризованих систем працюючих у реальному часі
Шпильовий Л.В. Математична модель та алгоритм екстремального управління процесом осадження дисперсної фази суспензії.
Тулученко Г.Я. Інформаційний модуль експрес-пошуку точок еквівалентності процесу нейтралізації.
Тернова Т.І. Урахування морфогенетичного рівняння в математичній моделі тканини.
Попруга А.Г. Теоретические и экспериментальные исследования электрических нагревателей по критерию экономии энергии.
Китаев А.В., Сушич Е.Ф. Приложение положений теории дросселя и трансформатора к расчету и анализу электромагнитом переменного тока.