УДК 62-50

Вступ. Гетероскедастичні процеси, тобто процеси із змінною в часі дисперсією, - поширений клас фінансово-економічних процесів, особливо в нестійкій перехідній економіці. За визначенням такі процеси відносяться до класу слабо нестаціонарних процесів, а тому описання їх даниміки має деякі особливості у порівнянні із стаціонарними. Одним із популярних підходів до моделювання нестаціонарних процесів є метод групового врахування аргументів [1], який був успішно застосований до побудови моделей ряду технічних, екологічних та економічних процесів. Частково питання побудови моделей нестаціонарних процесів розглянуто в роботах [2-7], однак моделювання гетероскедастичних процесів потребує докладного розгляду.

Метою даної роботи є розробка спрощеного тесту на гетероскедастичність, універсальної методики моделювання гетероскедастичних процесів, а також побудова моделей деяких реальних фінансово-економічних процесів та функцій прогнозування на їх основі.

1. Тестування на наявність гетероскедастичності. При моделюванні гетероскедастичних процесів спершу виконують перевірку на наявність гетероскедастичності. В літературі наведено кілька тестів на гетероскедастичність [6, 8, 9], які принципово не відрізняються один від одного, але потребують додаткових і не завжди оправданих обчислень. Найбільш зручним представляється тест, наведений нижче.

Спрощений тест на гетероскедастичність. Спрощений тест на гетероскедастичність складається з наступних кроків: (1) оцінити авторегресію y(k) = a0 + a0y(k-1) + e(k) або більш високого порядку, наприклад другого чи третього; (2) обудувати ряд {e2(k)}, скориставшись залишками від оцінювання попередньої моделі; (3) оцінити регресію:  e2(k) = a0 + a1 [0.4e (k-1) + 0.3e (k-2) + 0.2e (k-3) + 0.1e ( k-4)]; (4) якщо коефіцієнт a1 відмінний від нуля в статистичному смислі, тобто є значимим, то отримана модель для e2(k) описує гетероскедастичний процес.

Оскільки в цій моделі оцінюються тільки коефіцієнти  a1 і a0 а всі інші відомі (0.4; 0.3; 0.2; 0.1), то для визначення відмінності від нуля коефіцієнта a1 можна застосувати теорію перевірки гіпотези, тобто t-статистику для цього коефіцієнта.

Привабливість даного тесту полягає в простих обчисленнях і можливості застосування тієї ж теорії перевірки гіпотез, що використовується при аналізі лінійних моделей.

Сформулюємо постановку задачі оцінювання та прогнозування для авторегресійних умовно гетероскедастичних моделей АРКС(p,q) на основі максимізації функції правдоподібності.

Дана послідовність значень часового ряду . Для класу лінійних та псевдолінійних моделей АР(p) та АРУГ , , де  послідовність випадкових величин із змінною дисперсією;  послідовність випадкових величин з наступними властивостями: , 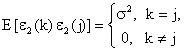необхідно знайти:

1) оцінку вектора параметрів  , мінімізуючи критерій , де ;

2) оцінки вектора  із умови максимізації функції правдоподібності ;

3) на основі оціненої моделі знайти оцінку прогнозу дисперсії:  ,використовуючи всю наявну інформацію на момент часу , із умови .

2. Методика побудови моделей гетероскедастичних процесів. Для прикладу розглянемо спочатку узагальнену авторегресійну модель гетероскедастичного процесу (УАРУГ). При використанні такої моделі умовна дисперсія процесу представляється за допомогою моделі авторегресії з ковзним середнім (АРКС). Нехай похибки моделі описуються рівнянням:

,                                                   (1)

де  процес білого шуму з одиничною (для простоти) дисперсією ;

                        .                          (2)

Оскільки процес  {} визначено в даному випадку як білий шум, то умовне і безумовне середнє процесу будуть дорівнювати нулю.

Математичне сподівання для :

                        .

Важливим моментом є те, що умовна дисперсія процесу  є залежною від часу:             , оскільки . Для того щоб ця умовна дисперсія була скінченою, необхідно щоб корені характеристичного рівняння, записаного для (2), знаходились всередині кола одиничного радіуса. Таким чином, основною відмінною властивістю моделі ОАРУГ є те, що умовна дисперсія збурень, які діють на процес , є процесом авторегресії з ковзним середнім.

Припустимо, що  - це процес авторегресії з ковзним середнім. При побудові моделі процесу в даному випадку можливі наступні варіанти:

-  якщо вдається побудувати адекватну модель АРКС, то похибки моделі будуть мати властивості білого шуму;

-  якщо не вдається побудувати адекватну модель АРКС, то, використовуючи автокореляційну функцію для квадратів залишків, необхідно побудувати модель УАРУГ, яка дозволяє виконати аналіз поведінки дисперсії процесу; корелограма процесу  дає можливість визначити присутність гетероскедастичності.

Оскільки , то рівняння (2) можна записати у формі:

.                              (3)

За своєю структурою це рівняння схоже на рівняння АРКС(q, p) для послідовності . Таким чином, методику побудови моделі гетероскедастичного процесу можна узагальнити наступним чином:

Крок 1. При необхідності зробити попередню обробку експериментальних даних (нормування, логарифмування, заповнення пропусків даних) і застосувати до них тести на гетероскедастичність. Якщо процес містить тренд, то перед побудовою моделі необхідно його видалити. Досить часто візуальний аналіз даних дозволяє отримати суттєву інформацію щодо присутності гетероскедастичності. Разом з візуальним аналізом необхідно розглядати параметри описової статистики, які полегшують визначення структури моделі.  

Крок 2. Користуючись АКФ та ЧАКФ для експериментальних даних, побудувати модель АР(p) або АРКС(p, q) для процесу  та обчислити ряд з квадратів залишків , де . Обчислити вибіркову дисперсію  збурення : , де  число залишків після побудови моделі АР чи АРКС.

Крок 3. Обчислити і побудувати графік вибіркової автокореляційної функції для квадратів залишків:

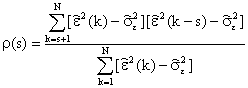            .                               (4)

Якщо існують такі значення , які відрізняються від нуля в статистичному смислі, то це свідчить про присутність процесу АРУГ або УАРУГ. Для того щоб переконатись у присутності гетероскедастичності, використовують статистику Люнга-Бокса, яка обчислюється за виразом [7]: , де  (емпіричне значення). Якщо значення  некорельовані, то  статистика повинна мати розподіл χ2 з  ступенями свободи.

Крок 4. Побудувати модель УАРУГ (або іншу модифікацію)

            ,                                      (5)

використовуючи ряд значень . Якщо в цій моделі хоча б один із коефіцієнтів  є значимим, то процес є дійсно гетероскедастичним. Оскільки модель (3.9) описує залишки моделі з деяким наближенням, то в загальному випадку доцільно продовжити процес уточнення моделей, що описують вихідний процес в цілому. Тобто, можна уточнити як початкову модель АР(p) чи АРКС(p, q), а також модель типу (2). Це робиться на наступному кроку.

Крок 5. Скористатись моделлю (5) для того щоб отримати дійсні значення залишків, які описуються цією моделлю, тобто згенерувати ряд . Згенерувати ще один ряд , де . За допомогою отриманого ряду побудувати уточнену модель процесу типу АР(p) чи АРКС(p, q). При необхідності процес уточнення моделей може бути продовжений.

            Приклад 2.1. Розглянемо побудову моделі УАРУГ для ряду  та моделі УАРУГ для скоригованого відносно імпульсних значень ряду . Для прикладу візьмемо дані, які характеризують щотижневий доход російської біржі сільгосппродуктів за 1996-1999 роки. Процедура обробки статистичних даних включає оцінювання параметрів математичних моделей на основі щотижневих чотирирічних даних, які використовуються для обчислення оцінки однокрокового прогнозу для дисперсії .

            На основі даного часового ряду оцінено моделі АР(р), потім УАРУГ(1,1), а також модель для доходу, що має структуру: , ~, .

Результати оцінювання наведено в таблиці 1. Параметри моделей оцінено методом максимальної правдоподібності. Діагностичні статистичні параметри , які наведені в двох останніх стовпчиках таблиці, свідчать про те, що моделі мають достатню степінь адекватності. Параметри  і  - це статистики Люнга-Бокса, які обчислені для визначення ступеня кореляції залишків моделі. Критичне значення для статистики визначається за допомогою таблиць для розподілу . На наступному кроці до оцінених моделей застосовується метод корекції моделі із врахуванням присутності суттєвих імпульсних значень ряду.

Таблиця 1

Результати оцінювання моделей АР(р) та АРУГ(1,1)

            В таблиці 2 наведено результати оцінювання тих же моделей, але вже із врахуванням корекції внаслідок присутності імпульсних значень.

Таблиця 2

Результати оцінювання моделей АР(р) та АРУГ(1,1) після корекції

            У порівнянні з таблицею 1 оцінки параметрів  і  змінились суттєво. Наприклад, для періоду даних 1996-1999 значення  зменшилось від 0,274 до 0,118, а значення  збільшилось від 0,468 до 0,694. Однак сума коефіцієнтів  суттєво не змінилась, що свідчить про те, що загалом динаміка зміни доходів є робастною по відношенню до імпульсних значень. На основі отриманих даних моделювання можна зробити висновок, що застосування корекції даних приводить до більш стійких оцінок параметрів.

Приклад 2.2. Ціни акцій на біржі. Розглянемо ряд ε2(k) - коливання цін акцій на біржі (рис.1; часткова АКФ наведена на рис.2).

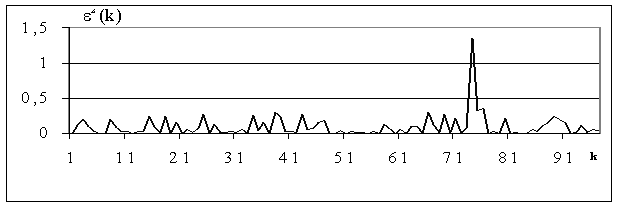
Рис.1. Коливання цін акцій на біржі

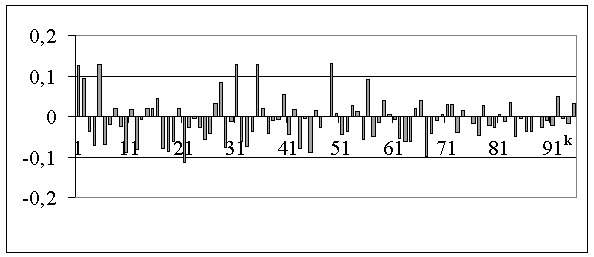
Рис.2. Часткова автокореляційна функція ряду

В результаті дослідження АКФ і ЧАКФ встановлено наступне:

1. Значення коефіцієнтів АКФ такі: ρ1 =  0,124 ; ρ2 = 0,107; ρ4 = -0,066; ρ5 = 0,103; ρ10 = -0,069.

2. Значення коефіцієнтів ЧАКФ мали такі значення: Ф1,1 = 0,124; Ф2,2 = 0,093; Ф4,4 = -0,072; Ф5,5 = 0,127; Ф10,10 = -0,91.

3. Для математичного опису процесу необхідно розглянути моделі АР(1), АР(2), АР(3) , АР(4). Найбільш вірогідні номери запізнювань, що входять до складу моделі: 1, 2, 4, 5, 10. У таблиці 3 наведені варіанти оцінювання декількох можливих структур регресійної моделі.

З таблиці 3 випливає, що найкраща модель, яка описує дисперсію з обчислених варіантів є АР(1, 2), оскільки для неї DW = 1,9899, R2 = 2,4041, АІС = - 0,7846. Таким чином, модель процесу має вигляд:  ε2(k) = 0,0769 + 0,1138 ε2(k-1) + 0,0927 ε2(k-2).

Значення RSS = 2,3826 і R2 = 0,0242 показує, що модель можна покращити за рахунок введення ковзного середнього. Варіанти оцінювання моделей з ковзним середнім наведені в таблиці 4.

З таблиці 4 випливає, що краща модель повинна обов’язково включати в себе ковзне середнє. З обчислених варіантів моделей кращою є АРКС((1, 2, 4, 5), (1)), оскільки для неї DW = 2,0675 , R2 = 1, АІС = - ∞. Крім того велике значення t-статистики для оцінок коефіцієнтів свідчить про їх значимість в статистичному смислі.

Таблиця 3

Варіанти оцінювання дисперсії вартості акцій однієї з компаній, що входять до числа провідних на Нью-Йоркській фондовій біржі за 1996 рік

Таблиця 4

Варіанти оцінювання моделей з ковзним середнім

Таким чином, модель, що адекватно описує дисперсію можемо записати як:

ε12(k) = 0,0714 + 0,1187 ε12(k-1) + 0,1123 ε12(k-2) - 0,096 ε12(k-4) + 0,1257 ε12(k-5) + ε2(k)

3. Прогнозування процесів за допомогою різницевих рівнянь 

Отримання функції прогнозування за допомогою розв'язку різницевого рівняння для процесу АРІКС(1,1,2):

.

Введемо наступне позначення:  і перепишемо задане рівняння як , розв’язок якого має вигляд: .  Знайдемо звідси : .

Розв’язок для моменту :         

.

Підставимо в цей розв’язок отриманий вище вираз для :

            .

Оскільки  , то

.

На основі останнього рівняння запишемо функцію прогнозування на один крок: , оскільки .

Функція прогнозування на два кроки:

,

і для довільного числа кроків прогнозування маємо:

.

Отримане рівняння – це рівняння прямої (її нахил визначається коефіцієнтом ), на яку накладається зважений випадковий процес. Для порівняння точності прогнозу на основі різницевих рівнянь скористаємось фільтром Калмана та методом, запропонованим в пакеті Eviews.

Розглянемо конкретні приклади застосування розробленої методики для побудови прогнозу поведінки дисперсії ряду.

Приклад 4.1. Розглянемо ряд, що описує дисперсію вартості акцій однієї з компаній, що входить до числа провідних на Нью-Йоркській фондовій біржі. На основі моделі, що адекватно описує процес

ε12(k)=0,0714 + 0,1187 ε12(k-1) + 0,1123 ε12(k-2) - 0,096 ε12(k-4) +  0,1257 ε12(k-5) + ε2(k),

яка отримана вище, побудовано прогноз вартості акцій на 5 кроків та порівняно його з реальними значеннями ряду. Графік прогнозу наведено на рис 3.

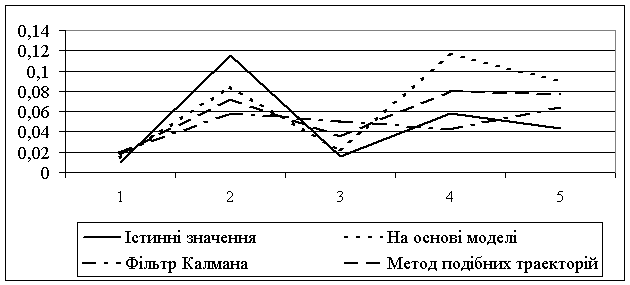
Рис. 3 Порівняльний графік прогнозу дисперсії вартості акцій однієї з компаній,

що входить до числа провідних на Нью-Йоркській фондовій біржі

Статистичні параметри отриманого прогнозу наведені в таблиці 5.

Таблиця 5

Таким чином, запропонований системний підхід може бути використаний при побудові математичних моделей процесів за часовими рядами та побудові прогнозів поведінки рядів, включаючи гетероскедастичні та нелінійні щодо змінних процеси. Для більшості моделей кращим є прогноз на основі моделі, але при прогнозуванні на один крок кращим є прогноз побудований за допомогою фільтра Калмана, що пояснюється вибором оптимального коефіцієнта фільтра.

Висновки. Розроблена методика ітеративної побудови моделей гетероскедастичних процесів на основі часових рядів, яка дає можливість отримати модель з високим ступенем адекватності для опису динаміки дисперсії часового ряду. Запропоновано метод подальшого підвищення адекватності моделей гетероскедастичних процесів у випадку присутності імпульсних адитивних складових часового ряду шляхом врахування цих складових при оцінюванні параметрів моделі. При цьому незначне ускладнення процедури оцінювання параметрів моделі дозволяє суттєво підвищити її якість. Наведено приклади використання запропонованої методики описання гетероскедастичних процесів до прогнозування конкретних фінансово-економічних процесів. Отримані результати прогнозування свідчать про їх високу якість, що дозволяє скористатись ними при прийнятті рішень щодо оперативного управління.

1.                  Ивахненко А.Г. Индуктивный метод самоорганизации моделей сложных систем. – Киев: Наукова думка, 1982. – 296 с.

2.                  Себер Дж. Прикладной регрессионный анализ. – М.: Мир, 1982. – 450 с.

3.                  Бард Й. Нелинейное оценивание параметров. – М.: Статистика, 1979. – 349 с.

4.                  Дрейпер Н., Смит Г. Прикладной регрессионный анализ (т.2). - М.: Финансы и статистика, 1986. - 366 с.

5.                  Бідюк П.І., Зворигіна Т.А. Структурний аналіз методики побудови регресійних моделей за спостереженнями часового ряду // Управляющие системы и машины, 2003, № 3, с.

6.                  Бідюк П.І., Половцев О.В. Аналіз та моделювання економічних процесів перехідного періоду. – Київ: НТУ КПІ, 1999. – 230 с.

7.                  Бідюк П.І., Баклан І.В., Рифа В.М. Системний підхід до побудови математичних моделей на основі часових рядів // Системні дослідження та інформаційні технології, № 3, 2002, с. 114-131.

8.                  Enders W. Applied econometric time series. - New York: John Wiley & Sons, Inc., 1995. - 434 p.

9.                  Johnston J., DiNardo J. Econometric methods. - New York: McGraw-Hill, Inc., 1997. - 530 c.