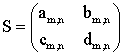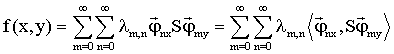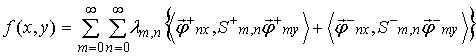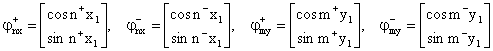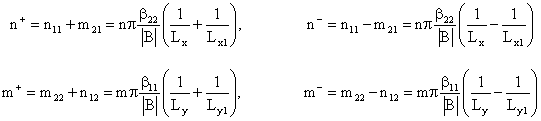УДК 677.05.059:621.3.078.08
УРАХУВАННЯ МОРФОГЕНЕТИЧНОГО РІВНЯННЯ В МАТЕМАТИЧНІЙ МОДЕЛІ ТКАНИНИ
Тернова Т.І.
Вступ. Підвищення якісних показників продукції легкої і зокрема текстильної промисловості зв'язано з кількісним і якісним розвитком її техніки і технології. Для успішного управління і контролю технологічними процесами і їхньої оптимізації широко застосовують методи технічної кібернетики. До числа цих методів у першу чергу відносяться методи математичного моделювання технологічних процесів, що включають методи одержання математичних моделей і їхнє дослідження.
Постановка проблеми. Тканина як об'єкт дослідження характеризується великим числом взаємозалежних факторів, наявністю істотних неконтрольованих збурювань і помилок виміру окремих факторів і випадковою зміною в часі характеристик. Тому її можна віднести до категорії складних об'єктів текстильної промисловості [1, 2].
Наявність математичної моделі об'єкта й алгоритму управління процесом забезпечує умови для більш швидкого інженерного конструювання раціональної системи автоматичного регулювання технологічного процесу, створення системи автоматичного технічного контролю процесів і управління агрегатами і потоковими лініями. Знаючи математичну модель процесу або об'єкта, можна спрогнозувати властивості вихідного продукту, оцінити ступінь впливу вхідних факторів з метою розробки схеми контролю і стабілізації найбільше що сильно впливають факторів, а також здійснити оптимізацію процесу.
Відсутність математичної моделі і недостатнє знання динамічних властивостей об'єктів приводить до інтуїтивного управління процесом, що відповідно відображається на продуктивності машин і якості продукту, що випускається.
Недосконалі гіпотези про моделі процесів і об'єктів і відсутність повного урахування факторів, що визначають вхідні впливи і властивості об'єкта, приводять до відхилення прогнозованих характеристик від характеристик продукту, одержуваного в реальних об'єктах. Математична модель вважається адекватною об'єктові, якщо з достатньою точністю відбиває його поводження, тобто зміну одного або декількох вихідних параметрів при варіюванні вхідних параметрів (факторів) у заздалегідь заданому діапазоні.
Одержання адекватної моделі тканини як об'єкта контролю, що враховує технологію одержання і топологію складного переплетення ниток, є актуальною проблемою при створенні автоматичних систем контролю й управління технологічно процесом і виробництвом.
Аналіз останніх досліджень і публікацій. В основу математичного опису тканини, як об'єкту контролю структурних характеристик покладено підхід, який розроблено в працях професора, д.т.н. А.П.Храпливого [3, 4].
Для опису тканини з ваговою функцією f(x, y), з огляду на періодичність по рапортам природно використовувати ряд Фур'є F{f(x, y}. Тоді модель f(x, y) описується для кінцевого числа додатків ряду [3]:
|
|
(1) |
Таким чином, при продовженні по рапортам, полотнину тканини можливо описати для повного ряду відомим виразом [5]:
|
|
(2) |
Враховуючи ортогональність структури тканини модель вигідно розглядати не як гармоніки що описують відгук на хвилю з максимумами на nх + mу = kp [5],
|
|
(3) |
а як реакцію на взаємодію хвиль за напрямком осей X, Y [4]. При цьому опис представляється як взаємодія одиничних векторів пов'язаних із системою утокових і основних ниток, що більш відповідає поставленій задачі.
|
|
(4) |
Тоді, як показано в роботах [3, 4] ядром є лінійний оператор, що відображає топологічні особливості об'єкту:
|
|
(5) |
Отже, модель тканини описується сумою білінійних форм [4], чим досягається збереження в моделі топологічних особливостей тканини:
|
|
(6) |
Зміна представлення моделі [4], дозволяє отримати більш простий запис елементів спектральних матриць Sіj [6]:
|
|
(7) |
У даному представленні виділяється вплив рівноважної - парної складовий рапорту, не рівноважної - непарної складовий та взаємних впливів.
Застосування розподілу моделі на компоненти верхніх і нижніх бічних смуг дозволяє зберегти однаковість побудови моделі і фізичну інтерпретацію елементів моделі [6]:
|
|
(8) |
При цьому як основній, так і утоковій системі ниток відповідають по два одиничних вектори:
|
|
(9) |
Істотним моментом є можливість завдяки використанню представлення (8) описати явище формування в деформованих текстильних матеріалах регулярних структур переважаючих розміри рапорту [6]:
|
|
(10) |
Отже, при деформації тканини в її структурі виникають більш великі, чим одиничний рапорт регулярні структури, що визначає зміну властивостей тканини в межах полотнини. З іншої сторони вираження (10) дозволяє підкреслити вплив малих деформацій, як випадкового фактора.
Виходячи з аналізу останніх публікацій і розробок, можна зробити висновок, що існуючі в даний час математичні моделі не відображають повною мірою технологію одержання готової тканини.
Ціллю статті є уточнення математичної моделі тканини, що буде враховувати технологію одержання готової тканини і текстуру складного переплетення ниток.
Технологічний процес з погляду одержання морфогенетичного рівняння.
Доцільно одержати математичну модель контрольованої тканини виходячи з технології одержання готової тканини. Такий підхід дозволить враховувати всі структурні особливості тканини, що тією чи іншою мірою впливають на формування плоского зображення відсканованої ділянки рапорту для подальшого його контролю. Це особливо актуально для систем з елементами штучного інтелекту працюючих за принципом перевірки гіпотез. Такі системи добре розпізнають об'єкти, що знають у тім значенні, що знають, як вони улаштовані і яким чином можуть піддаватися деформаціям і перекручуванням. У цьому змісті, чим краще система знає внутрішню структуру об'єкта контролю, тим якісніше буде результат розпізнавання.
Іншою не менш важливою перевагою одержання математичної моделі тканини, що враховує технологію одержання складного переплетення ниток є можливість застосовувати її в технічних системах зору незалежно від конструктивних і фізичних особливостей датчиків. Тобто така модель враховує особливості одержання контрольованого зображення не тільки телевізійними системами, але і системами контролю фізичних полів, лазерними, інфрачервоними й ін. [7, 8]
Незважаючи на удавану простоту, процес формування тканини є складним. Принципова його сутність не залежить від виду вироблюваної тканини і типу ткацького верстата, на якому вона виробляється [9-11]. Сутність процесу ткацтва полягає у взаємному переплетенні основних і утокових ниток у заданій послідовності. Причому основні й утокові нитки розташовують, як правило, взаємно перпендикулярно. Процес ткацтва є циклічним і включає п'ять операцій, що повторюються при формуванні кожного елемента тканини. Одна утокова нитка і система основних ниток, що згинаються і розтягуються при взаємних охопленнях і контактах, утворять цей своєрідний міцний елемент структури ткацького переплетення.
Процес формування складається з наступних операцій [10]: зевоутворення, прокладання утокової нитки в зев, прибій утокової нитки до опушки тканини, відвід елемента тканини з зони формування і компенсація витраченої основи на утворення елемента тканини. Останні дві операції здійснюються при подовжньому русі тканини й основи, слідом за прибоєм утоку або разом з цією операцією.
Стабільність процесу формування тканини і задана структура її забезпечується визначеним заправним (початковим) натягом основи, оптимальною заправною лінією ткацького верстата і взаємним розташуванням робочих органів при формуванні тканини, моментом вступу їх у циклі роботи ткацького верстата, тобто залежать параметрів заправлення верстата, параметрів процесу і структури тканини. Усі технологічні операції здійснюються робочими органами (механічної, пневматичної або гідравлічної дії), кінематичні і динамічні характеристики руху яких мають велике значення для забезпечення стабільності формування тканини.
Робочі органи ткацького верстата приводяться в дію (прямування) спеціальними механізмами. У залежності від призначення всі механізми ткацького верстата можна розділити на три групи: 1) основні механізми, що забезпечують виконання основних технологічних операцій у процесі формування тканини; до них відносяться: зевоутворювальний, бойовий, батаний механізми і механізми натягу і відпустки основи і навівання тканини; 2) додаткові механізми, що забезпечують підвищення продуктивності верстата; до них відносяться механізми живлення верстата утоком; 3) запобіжні механізми, що попереджають виникнення браку тканини і поломки деталей верстата.
Найбільш загальний процес переплетення ниток у тканині реалізується на ткацькому верстаті, що складається з п'яти основних частин [12]:
1. Котушка, на яку намотується основа тканини.
2. Ремізи, через які проходить основа тканини. Кожна рамка ремізу може бути піднята (або опущена), щоб пропустити нитку, що наповнює, над (або під) основою.
3. Човник, який веде нитку, що наповняє, (уток).
4. Бьодро, функція якого полягає в проштовхуванні або закріпленні нитки, що наповняє, у вже витканій матерії.
5. Котушка, на яку приймається готова тканина.
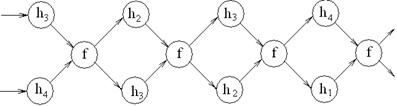
Щоб формально виразити образи рухів при переплетенні ниток у тканині, будемо вважати утворюючими основні рухи, розбиті на два класи [12]:
|
|
(11) |
Тут
|
|
(12) |
де hi – рух, що представляє підняття рами i-го ремізу,
fi – просування човника з j-й ниткою, що наповняє.
Нехай ![]() позначає сукупність перегинів ниток основи. Розглянемо розбивку:
позначає сукупність перегинів ниток основи. Розглянемо розбивку:
|
|
(13) |
на непересічні підмножини. Конфігурації, що складаються з «h» і «f», формують образи тканини.
Образи руху реміз, що породжують плоске зображення.
Образи руху породжують плоскі образи тканини. Для того щоб їх ідентифікувати, будемо застосовувати правило ідентифікації, що засноване лише на значенні сорту нитки, видимій на кожнім з перетинань основи з наповнювачем. При цьому ми нехтуємо деякими властивостями результуючої тканини, але зберігаємо всю існуючу комбінаторну інформацію.
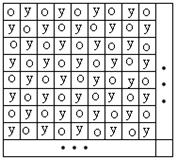
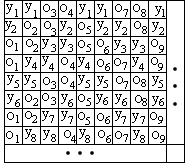
Якщо є лише 2 ремізи, r=2, і один наповнювач s=1, то можна одержати простий образ тканини шляхом періодичного повторення конфігурації руху, приведеної на малюнку 1а (![]() ). Нитки основи проходять через ремізи 1 і 2 перемежованому порядку. При цьому образи руху формують плоский образ, показаний на рисунку 1б.
). Нитки основи проходять через ремізи 1 і 2 перемежованому порядку. При цьому образи руху формують плоский образ, показаний на рисунку 1б.
|
а) |
|
|
|
б) |
|
Рис. 1 Проста тканина: а) образи рухів, що породжують плоский образ тканини; б) плоский образ тканини. |
Математичний опис даного простого переплетення повністю відповідає математичної моделі викладеної вище.
Зрозуміло, дана модель не вичерпує всі можливі види переплетення ниток при формуванні тканин.
Твілові тканини вимагають, принаймні, 3 ремізи. На рисунку 2а,в показаний трьох вальний твіл, і отриманий плоский образ має діагоналі, типові для твіла [12].
Можна одержати більш складні форми, варіюючи діагональ за допомогою зміни в основі. Одна з таких варіацій показана на рисунку 2 б,г. У ній використовуються 4 ремізи, у яких порядок ниток основи встановлюється різницями ...5,3,5,3,5,3,... так, що, відправляючись від нитки 1, ми одержуємо 1,6,9,14,17,... .
Просторово-тимчасова конфігурація має цикл, як це показано на малюнку 2г, причому ремізи чергуються додатком 1 по модулю 4. На малюнку цим рухам відповідають образи у вигляді «ялинки».
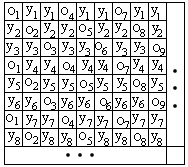
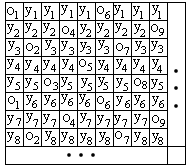
Для сатину необхідні принаймні 5 ремізів [12], оскільки при меншому їхньому числі одержують лише твілові образи. Приклад атласу з п'ятьма валами приведений на рисунку 4, де порядок ниток основи задається різницями ... 5,5,5, ... так, що, відправляючись від нитки 1, ми одержуємо для першої ремізи 1,6,11,16, ... і т.д. Часова послідовність для ремізів задається додатком 3 по модулю 5. Результат буде залежати від того, що буде переважати – основа або утік.
|
||||||||||||||
Отриманий плоский образ є п’ятивальним сатином. Відзначимо, що дана структура типова для атласу, вона має тенденцію відбивати світло і додає блиску поверхні тканини.
Морфогенетичне рівняння тканини.
Розглянемо загальний випадок руху при формуванні переплетень ниток як зображення на просторово-часовому тлі, тоді в момент часу t маємо
|
|
(14) |
коли ремізу h(t) піднята, після чого рухається човник з утоком f(t). Значеннями f є натуральні числа, але значення h становлять підмножини W. Нехай x – координатна вісь, що перетинає основу, а y – інша координатна вісь, перпендикулярна їй. Цілі значення x і y (тут використовуються тільки цілі значення) відповідають перетинанням основи й утоку. Якщо ототожнити y з t, то просторово-часове зображення, що задається формулою (14), робить просторове (або, скоріше, плоске) зображення I.
|
|
|
а)
|
|
|
|
б) |
|
Рис. 3 Атлас, отриманий з використанням 5 реміз: а) образи рухів, що породжують плоский образ тканини; б) плоский образ тканини. |
Якщо показується x-нитка основи із значенням w(x), то це означає, що вона піднята ремізою, через яку вона просмикується. У противному випадку уток f=f(y). Отже,
|
|
(15) |
або
|
|
(16) |
де символ In означає індикаторну функцію виразу, що знаходиться у фігурних дужках.
Співвідношення (16) перетворить зображення руху ![]() в плоске зображення Im і є морфогенетичним рівнянням. У випадку тканини морфогенетичне рівняння, що керує синтезом образів виявляється досить простим, на відміну від аналогічних рівнянь для інших комбінацій засобів і матеріалу.
в плоске зображення Im і є морфогенетичним рівнянням. У випадку тканини морфогенетичне рівняння, що керує синтезом образів виявляється досить простим, на відміну від аналогічних рівнянь для інших комбінацій засобів і матеріалу.
Математична модель тканини, що враховує технологію переплетення ниток.
Для урахування топології форми переплетення ниток у рівняння моделі тканини потрібно ввести оператор топології ![]() , який буде враховувати яка саме нитка основи чи утоку в результаті їх перекручування або перетинання буде знаходитись в полі поверхневого візуального спостереження. Таким чином, модель тканини, що враховує технологію ткацтва, буде описуватися рівнянням:
, який буде враховувати яка саме нитка основи чи утоку в результаті їх перекручування або перетинання буде знаходитись в полі поверхневого візуального спостереження. Таким чином, модель тканини, що враховує технологію ткацтва, буде описуватися рівнянням:
|
|
(17) |
де ![]() - оператор, що відображає технологію переплетення ниток.
- оператор, що відображає технологію переплетення ниток.
Для узгодження розмірності координат морфогенетичного рівняння (16) з оператором топології ![]() в рівнянні моделі тканини (17) запровадимо масштабні коефіцієнти:
в рівнянні моделі тканини (17) запровадимо масштабні коефіцієнти:
|
|
(18) |
де n, m – задається розкладанням у ряд Фур'є;
![]() – масштабний коефіцієнт, що узгоджує координати морфогенетичного рівняння з координатами ряду Фур'є по осі x (уздовж утоку);
– масштабний коефіцієнт, що узгоджує координати морфогенетичного рівняння з координатами ряду Фур'є по осі x (уздовж утоку);
![]() – масштабний коефіцієнт, що узгоджує координати морфогенетичного рівняння з координатами ряду Фур'є по осі y (уздовж основи).
– масштабний коефіцієнт, що узгоджує координати морфогенетичного рівняння з координатами ряду Фур'є по осі y (уздовж основи).
Індикаторний вираз, що враховує технологію переплетення ниток відбиває алгоритм формування текстури переплетення й у загальному вигляді буде виглядати в такий спосіб:
|
|
(19) |
де ![]() - послідовність руху реміз, що створює задане переплетення ниток для визначеного вигляду тканини.
- послідовність руху реміз, що створює задане переплетення ниток для визначеного вигляду тканини.
Для розглянутих тканин значення![]() представлені в таблиці 1.
представлені в таблиці 1.
Таблиця 1
Послідовність руху реміз, що створює топологію переплетення ниток
|
Вид тканини |
Кількість реміз |
Послідовність руху реміз |
|
Твіл |
3 |
|
|
Твіл |
4 |
|
|
Сатин |
5
|
|
Утворюючим, представленим у моделях руху на малюнках, відповідає певна арність. Розмір арності являє собою суму вхідної арності ![]() і вихідної арності
і вихідної арності ![]() :
:
|
|
(20) |
У прикладах переплетення ниток арність не обмежується простою конфігурацією рівної двом. Також варто враховувати, що не всі регулярні конфігурації мають однакову вагу. Для введення міри на просторі конфігурацій необхідно визначити розподіл імовірностей. У випадку метричної теорії образів комбінаторні властивості приводять до певних імовірнісних наслідків. Розглянемо простір ![]() і довільне джерело утворюючих, так що на множині утворюючих G заданий апріорний розподіл q. Нехай
і довільне джерело утворюючих, так що на множині утворюючих G заданий апріорний розподіл q. Нехай ![]() - добуток мір на прямому добутку просторів
- добуток мір на прямому добутку просторів ![]() , причому q – безумовний розподіл по кожній координаті.
, причому q – безумовний розподіл по кожній координаті.
Якщо ![]() , то розподіл імовірностей
, то розподіл імовірностей ![]() визначається на сукупності регулярних конфігурацій як умовна міра.
визначається на сукупності регулярних конфігурацій як умовна міра.
|
|
(21) |
Тут для n утворюючих ![]() , що входять у припустимі n-елементарні конфігурації, уводиться фіксована індексація, що вибирається в залежності від використовуваного типу з'єднання. Користуючись такою індексацією, можна розглядати
, що входять у припустимі n-елементарні конфігурації, уводиться фіксована індексація, що вибирається в залежності від використовуваного типу з'єднання. Користуючись такою індексацією, можна розглядати ![]() як точку в просторі
як точку в просторі ![]() і W – в якості підмножини
і W – в якості підмножини ![]() .
.
Підставимо отриманий вираз (18) у рівняння математичної моделі тканини (17). Одержимо:
|
|
(22) |
Отримана модель враховує не тільки топологічні особливості тканини, але і технологію формування конкретного виду переплетення.
Якщо ми відкинемо фігурні дужки в рівнянні (18) і змінимо ліву частину, заміняючи x на -x, то одержимо плоске зображення на зворотній стороні тканини. Таким чином, підставивши отримане зображення виворітної сторони тканини в рівняння (17) можна одержати модель тканини, зручну при додатковому контролі готової тканини з вивороту.
Висновки:
1. Отримано узагальнену математичну модель тканин складного переплетення, що враховує технологію переплетення ниток (22).
2. З аналізу отриманих формул (18) і (22) можна зробити висновок, що отримана модель тканини відображає структуру готової тканини і дозволяє використовувати її при візуальному автоматичному контролі готових тканин, як з лицьової поверхні, так і з виворітної, що підвищить якість розбраковування.
3. Отримана математична модель тканини як об'єкту контролю забезпечує умови для більш швидкого інженерного конструювання раціональної системи автоматичного регулювання технологічного процесу, створення системи автоматичного технічного контролю процесів і управління агрегатами і потоковими лініями.
4. Отриману математичну модель структури тканини можна використовувати в системах технічного зору з використанням компенсації інформаційних потоків для підвищення відсотка правильного розпізнавання.
5. Аналіз сигналу неузгодженості в системах з компенсацією, що використовують отриману модель дозволяє судити про поточний стан устаткування ткацтва, що дозволить скоротити відсоток браку за рахунок виключення поступових відмовлень устаткування і своєчасного налагодження робочих органів ткацького верстата.
6. Отримана математична модель тканини (22) чутлива до різниці між переплетенням нитки основи з ниткою утоку і їхнім перетинанням, що особливо важливо при контролі візуальних показників системами з телевізійними датчиками.
In given article are considered questions of building mathematical models fabrics with provision for technologies of production fabric. Analysed motion models, which generate a topology of binding the threads in weaving. Received mathematical model fabrics, which takes a topology of binding the threads into account.
1. Севостьянов А.Г. Методы и средства исследования механико-технологических процессов текстильной промышленности. - М.: Легкая индустрия, 1980. – 392 с.
2. Anagnostopoulos C. et al., “High Performance Computing Application for the Textile Quality Control”, to be appeared in the International Conference on Intelligent Information Processing (IIP 2000) proceedings, Federated Conference of the World Computer Congress (WCC 2000), 21-25 August 2000, Beijing, China.
3. Храпливый А.П. Теоретические основы и практика разработки систем и средств контроля и управления структурными показателями тканей. Диссертация на соискание ученой степени д-ра. тех. наук: 05.13.07 - Ленинградский ордена Трудового Красного Знамени институт текстильной и легкой промышленности им. C.М. Кирова, 1990 г.
4. Храпливий А.П. Телевизионный датчик для контроля качества тканей // Микропроцессоры и устройства автоматики в системах управления электроприводами. - Иваново. - 1983. – 84 с.
5. Будак Б.М., Фомин С.В. Кратные интегралы и ряды. - М., 1967. - 606 с.
6. Рожков С.А., Куцак Р.С., Бражник Д.А. Описание объекта как двумерной структуры с продолжением по рапортам Проблемы легкой и текстильной промышленности Украины, №1 (8), 2004 г., с.274-281.
7. Храпливий А.П., Бражник О.М., Тернова Т.І. Засоби побудови систем автоматичної розбраковки тканин //Технологія, автоматизація та економіка в переробній галузі. Міністерство освіти України, Інститут змісту і методів навчання, Херсонський державний технічний університет. Київ, 1998. с.86-90.
8. Тернова Т.І. Методи контролю поверхні текстильних матеріалів // Тезисы докладов международной научно-практической конференции «Проблемы легкой и текстильной промышленности Украины». - Херсон, 2005. Проблемы легкой и текстильной промышленности Украины, №1 (10), 2005 г., с.276.
9. Прядение хлопка и химических волокон (проектирование смесей, приготовление холстов, чес. и греб. ленты): Учебник для вузов / И.Г.Борзунов, К.И.Бадалов, В.Г.Гончаров:- 2-е изд., перераб. и доп .- М: Легкая и пищевая промышленность, 1982. – С. 376.
10. Механическая технология текстильных материалов: учеб. для втузов / А.Г.Севостьянов, Н.А.Осьмин, В.П.Щербаков и др.-М.: Легпромбытиздат 1995.-512с.:ил.)
11. Справочник по хлопкопрядению /Широков В.П., Владимиров Б.М., Полякова Д.А. и др.-5-е изд. перераб. и доп.- М.: Легкая и пищевая промышленность, 1985,-427с.
12. У. Гренандер Лекции по теории образов. Перевод с англ. Под ред. Ю. Журавлева, Издательство «МИР», - :М. 1979
Ответы на вопросы [_Задать вопроос_]
Читайте также
Моделирование объектов и систем управления
Соколов А.Е., Махова Е.О. Моделирование процесса принятия педагогического решения при компьютеризированном обученииСлавко О.Г. Порівняльний аналіз керування регулятором на основі локальної моделі керованого процесу та П-регулятором
Войтенко В.В., Дикусар Е.В, Ситников В.С. Определение частоты среза устройства сглаживания данных на основе метода скользящего среднего
Передерій В.І. Алгоритм визначення та оцінки характеристик ефективності комп’ютерних систем на початковій стадії проектування в умовах невизначенності
Ляшенко С.А, Ляшенко А.С. Оценка модели псевдолинейной регрессии
Ладієва Л.Р. Математична модель процесу газової мембранної дистиляції
Носов П.С., Косенко Ю.І. Нечіткі моделі і методи ідентифікації та прогнозу стану інформаційної моделі студента
Китаев А.В., Глухова В.И. Анализ работы синхронного двигателя с неявнополюсным ротором по данным каталога
Дорошкевич В.К., Пироженко А.В., Хитько А.В., Хорольский П.Г. К определению требований к системам увода космических объектов
Голінко І.М., Ковриго Ю.М., Кубрак А.І. Настройка системи керування за імпульсною характеристикою об’єкта
Яшина К.В., Садовой А.В. Комплексная математическая модель тепловых процессов, происходящих в дуговых электросталеплавильных печах
Шейник С.П., Рудакова А.В. Использование функций принадлежности для моделирования параметров распределенных объектов
Хомченко А.Н., Литвиненко Е.И. Метод барицентрического усреднения граничных потенциалов электростатического поля
Селяков Е. Б. Моделирование требований к техническим системам методами математической логики
Тодорцев Ю.К., Ларіонова О.С., Бундюк А.М. Математична модель контура теплопостачання когенераційної енергетичної установки
Кириллов О.Л. , Якимчук Г.С. Моделирование процесса управления системой перегрузки углеводородных жидких топлив
Шеховцов А.Н., Козел В.Н. Построение математической модели формирования распределенных систем
Китаев А.В., Глухова В.И. Анализ поведения генератора постоянного тока по данным каталога
Хомченко А.Н., Козуб Н.О. Задачі наближення функцій: від лагранжевих до серендипових поліномів
Хобин В.А., Титлова О.А. Определение температуры парожидкостной смеси в дефлегматоре АДХМ по результатам измерений температуры его поверхности
Григорова Т.М., Усов А.В. Вероятностно-статистическое моделирование маршрутизированных пассажиропотоков в крупных городах
Горач О.О., Тернова Т.І. Моделювання технологічного процесу одержання трести при використані штучного зволоження з урахуванням складу мікрофлори
Дубік Р.М., Ладієва Л.Р. Математична модель розділення неоднорідних рідких систем
Казак В.М, Лейва Каналес Родриго, Яковицкая Е.Ю. Моделирование динамики полета магистрального самолета на исследовательском стенде
Завальнюк И.П. Исследование процесса торможения автомобиля как критического режима динамической системы
Дмитриев С.А., Попов А.В. Построение портрета неисправностей проточной части газотурбинного двигателя на примере АИ-25
Русанов С.А., Луняка К.В., Клюєв О.І., Глухов Г.М. Математичне моделювання робочого процесу в апаратах з віброкиплячим шаром та розробка систем автоматизованого моделювання гідродинаміки віброкиплячих шарів
Боярчук В.П., Сыс В.Б. Экспериментальные исследования влияния технологии шлихтования на изменение жесткости текстильных нитей
Селін Ю.М. Використовування контекстних марківських моделей для аналізу дії промислових вибухів на будівельні конструкції
Рудакова А.В. Проблемы интеграции сложных систем
Передерій В.І., Касап А.М. Математична модель та алгоритм автоматизації розрахунку параметрів комп’ютеризованих систем працюючих у реальному часі
Передерий В.И., Еременко А.П. Математические модели и алгоритмы принятия релевантных решений пользователями автоматизированных систем с учетом личностных и внешних факторов на базе генетических алгоритмов
Михайловская Т.В., Михалев А.И., Гуда А.И. Исследование правил клеточных автоматов для моделирования процессов затвердевания квазиравновесных бинарных сплавов
Хомченко А.Н., Колесникова Н.В. Явление «сверхсходимости» в задаче Прандтля для уравнения Пуассона
Китаев А.В., Глухова В.И. Анализ работы трансформатора по данным каталога
Квасницкий В.В., Ермолаев Г.В., Матвиенко М. В., Бугаенко Б.В., Квасницкий В.Ф. Оценка применимости метода компьютерного моделирования к исследованию напряженно-деформиррованного состояния цилиндрических узлов
Китаев А.И., Глухова В.И. Анализ работы асинхронного двигателя по данным каталога
Шелестов А.Ю Имитационная модель взаимодействия GRID-узлов с очередью доступа к общей памяти
Chizhenkova R.A. Mathematical Aspects of Bibliometrical Analysis of Neurophysiological Investigations of Action of Non-ionized Radiation (Medline-Internet)
Хомченко А.Н., Козуб Н.А. Геометрическое моделирование дискретных элементов с криволинейными границами
Славич В.П. Модель автоматизованої системи управління потоками транспортних засобів
Маркута О.В., Мысак В.Ф. Программная реализация и исследование особенностей метода группового учета аргументов
Степанкова Г.А., Баклан І.В. Побудова гібридних моделей на основі прихованих марківських моделей та нейронних мереж
Бакшанська Т.Д., Рижиков Ю.Г., Тодорцев Ю.К. Математична модель процесу горіння природного газу з рециркуляцією продуктів згорання для цілей управління
Хомченко А.Н. Новые решения обобщенной задачи Бюффона
Передерий В.И., Еременко А.П. Математические модели и алгоритмы определения релевантности принимаемых решений с учетом психофункциональных характеристик пользователей при управлении автоматизированными динамическими системами
Ложечников В.Ф., Михайленко В.С., Максименко И.Н. Аналитическая много режимная математическая модель динамики газовоздушного тракта барабанного котла средней мощности
Ковриго Ю.М., Фоменко Б.В., Полищук И.А. Математическое моделирование систем автоматического регулирования с учетом ограничений на управление в пакете Matlab
Исаев Е.А., Наговский Д.А. Математическое описание влияния кривизны контактирующих тел на угол смачивания жидкости в межчастичном пространстве
Бідюк П.І., Литвиненко В.І., Кроптя А.В. Аналіз ефективності функціонування мережі Байєса
Тищенко И.А., Лубяный В.З. Математическое моделирование вокодера для определения оптимальной формы импульса сигнала возбуждения.
Николаенко Ю.И., Моисеенко С.В. Моделирование гармонического полиномиального базиса гексагона.
Козуб Н.А., Манойленко Е.С., Хомченко А.Н. Температурный тест для модифицированных базисов бикубической интерполяции.
Клименко А.К. Об упрощенном численном конструировании обратной модели динамического объекта.
Китаев А.В., Сушич Е.Ф. Расчет погрешностей измерительных трансформаторов.
Передерій В.І.,Касап А.М. Математична модель та алгоритм автоматизації розрахунку параметрів комп’ютеризованих систем працюючих у реальному часі
Шпильовий Л.В. Математична модель та алгоритм екстремального управління процесом осадження дисперсної фази суспензії.
Тулученко Г.Я. Інформаційний модуль експрес-пошуку точок еквівалентності процесу нейтралізації.
Попруга А.Г. Теоретические и экспериментальные исследования электрических нагревателей по критерию экономии энергии.
Китаев А.В., Сушич Е.Ф. Приложение положений теории дросселя и трансформатора к расчету и анализу электромагнитом переменного тока.