УДК 62-50
ПРОГРАММНАЯ РЕАЛИЗАЦИЯ И ИССЛЕДОВАНИЕ ОСОБЕННОСТЕЙ МЕТОДА ГРУППОВОГО УЧЕТА АРГУМЕНТОВ
Маркута О.В., Мысак В.Ф.
Стремительное развитие компьютерной техники существенно расширяет сферу использования методов математического моделирования для проектирования и управления сложными технологическими (техническими, экономическими, экологическими, финансовыми и др.) системами, прогнозирования результатов их деятельности, создания экспертно-диагностических подсистем и тренажерных комплексов по обучению персонала и т.п.
Эффективное использование методов моделирования требует простых и адекватных, как правило, формальных математических моделей. Одним из универсальных экспериментальных методов идентификации многомерных систем, применимым в режиме нормальной эксплуатации объектов исследования, есть метод группового учета аргументов (МГУА) [1,2]. Полученные по этому методу модели отображают неизвестные закономерности функционирования исследуемого объекта (вида “n входов – 1 выход”), информация о котором неявно содержится в выборке экспериментальных данных. В МГУА для построения моделей применяются принципы автоматической генерации вариантов, промежуточных решений и последовательной селекции лучших моделей по определенным критериям. Алгоритм метода основан на делении выборки на части, при этом оценивание параметров и проверка качества моделей выполняются на разных подмножествах экспериментальной выборки. Эффективность метода подтверждена решением многочисленных реальных задач в таких областях как экология, гидрометеорология, экономика, техника [3].
Согласно МГУА решение трудоемкой задачи получения n-мерной (по входам) модели заменяется многостадийным процессом решения большого числа относительно простых задач аппроксимации экспериментальных данных функциями двух переменных. На каждой из стадий производится отбор наилучших полиномов, которые используются на последующих стадиях в качестве фиктивных аргументов новых полиномов.
Подобная процедура построения сложной функции от полинома продолжается до тех пор, пока на какой-либо из стадий не будет достигнута заданная точность аппроксимации.
Вместе с тем метод имеет ряд особенностей, не получивших строгого математического обоснования и требующих оперативного уточнения под конкретные условия использования получаемой модели. К таким особенностям относятся влияние на адекватность модели уровня шумов, количества отбираемых полиномов, размерности задачи, размеров подмножеств и т.п. Трудоемкая процедура таких уточнений требует использования современных программных средств моделирования.
В статье представлена программная реализация МГУА с генерированием исходных данных, ориентированная на широкий спектр возможных применений, и проведены исследования:
· определение возможных пределов работы приложения (максимального числа факторов);
· исследование влияния шума на точность полученной модели;
· исследование влияния количества отбираемых наилучших частных описаний на каждом шаге;
· исследование влияния размеров подмножеств экспериментальных данных на точность искомой модели;
· влияние вида частных описаний на качество полученной модели.
1. Программная реализация МГУА
Для исследования метода группового учета аргументов была выполнена его программная реализация. Разработанное приложение решает задачу построения модели объекта (вида “n входов – 1 выход”) по выборке экспериментальных данных.
На рис.1 показана общая блок-схема алгоритма работы приложения.
Алгоритмы МГУА воспроизводят схему массовой селекции. Входные аргументы и промежуточные переменные сопрягаются попарно, и сложность комбинаций на каждом ряду обработки информации возрастает (как при массовой селекции), пока не будет получена единственная модель оптимальной сложности [1].
Алгоритм работы программы:
Этап 1. Искусственная генерация исходных (экспериментальных) данных.
На этом этапе производится генерация значений векторов аргументов. При этом начальное количество аргументов (n) и размер выборки (число точек условного эксперимента) N изначально заданы. Количество аргументов n задается непосредственно, а размер выборки N определяется как сумма размеров трех ее подмножеств: обучающего (N1), проверочного (N2) и контрольного (N3):
![]() (1)
(1)
Значения аргументов хі генерируются в соответствии со следующим выражением:
![]() (2)
(2)
где αi и φi каждый раз генерируются псевдослучайным образом из множеств [-A; A] и [-Fi; Fi] соответственно, где значения A и Fi изначально задаются.
Полученные векторы аргументов содержат нормированные псевдослучайные значения.
Значения yl генерируются следующим образом:
![]() (3)
(3)
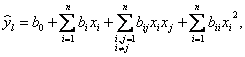 (4)
(4)
![]() , (5)
, (5)
где bi и Shl каждый раз генерируются псевдослучайным образом из множеств [-В; В] и [-Sh; Sh], где значения В и Sh изначально задаются. Параметр Sh содержит значение уровня зашумления в % от величины значений yl.
Этап 2. Реализация алгоритма МГУА.
Из множества аргументов x=(x1, x2,..,xn) выбираются пары аргументов (xi,xj) i,j=1,n; i≠j. Для них составляются функции частных описаний квадратичного вида [1]:
![]() (6)
(6)
Используя метод наименьших квадратов (МНК) [4] для каждого описания по обучающему подмножеству (![]() ) находится вектор неизвестных коэффициентов
) находится вектор неизвестных коэффициентов ![]() .
.
По полученным моделям каждого частного описания вычисляются значения ординат (вектор ![]() ) для всех точек проверочного подмножества
) для всех точек проверочного подмножества ![]()
.
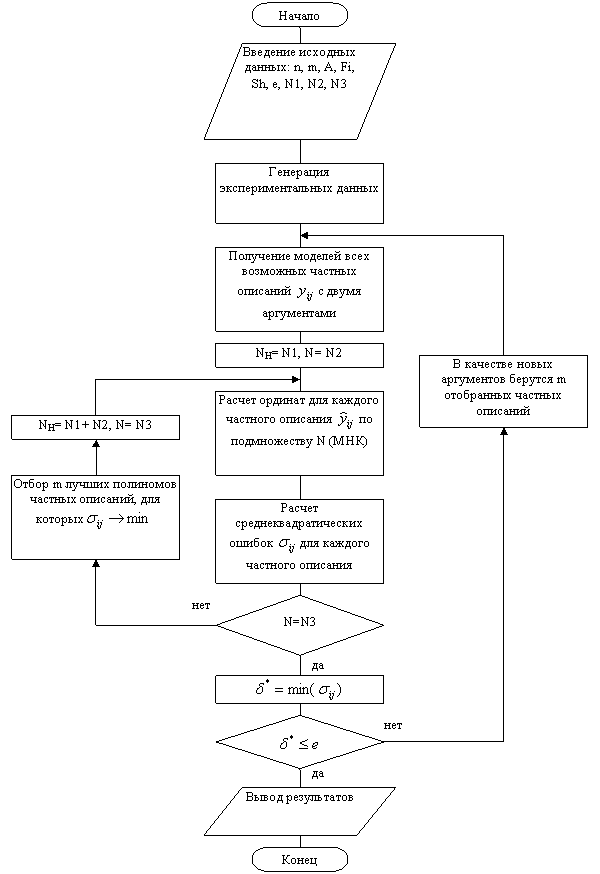
Рис. 1. Структурная блок-схема алгоритма разработанного приложения.
Далее производится расчет критерия селекции (среднеквадратической ошибки) для каждого частного описания по формуле:
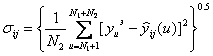 (7)
(7)
По критерию минимума на проверочном подмножестве отбираются m лучших моделей, т.е. реализуется процедура селекции.
Для отобранных моделей вычисляются значения ординат ![]() по контрольному подмножеству
по контрольному подмножеству ![]() .
.
Далее для них вычисляются значения критерия селекции (так же по контрольному подмножеству):
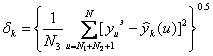 (8)
(8)
Находится ![]() .
.
Этап 3. Вывод результатов.
Производится вывод результатов в соответствующее поле окна приложения.
Выполняется проверка критерия останова:
![]() (9)
(9)
где ε = е (наперед заданная величина).
Если условие выполняется, то процесс поиска модели ![]() считается завершенным. В противном случае производится возврат на начало этапа 2 с предварительным пересчетом векторов аргументов (в качестве новых аргументов используются отобранные модели частных описаний).
считается завершенным. В противном случае производится возврат на начало этапа 2 с предварительным пересчетом векторов аргументов (в качестве новых аргументов используются отобранные модели частных описаний).
2. Определение возможных пределов работы приложения (максимального числа факторов)
Число факторов (входов объекта) в принципе не ограничено. На практике работа приложения была проверена до n = 25. Но при таком количестве аргументов наблюдалось существенное увеличение времени работы программы (длительности всех необходимых расчетов). Если при n=3, m=3 время, затраченное на расчет одного шага алгоритма, составляло доли секунды, а загрузка ЦП составляла 11%, то при n=25 и m=3 время расчета одного шага увеличилось до 40 секунд, а загрузка ЦП – до 100%.
Вообще ограничения в отношении числа факторов могут накладываться только исходя из технических характеристик компьютера, на котором производится расчет модели программой. С увеличением числа факторов резко возрастает число их частных описаний и, следовательно, объем обрабатываемой информации, что в свою очередь вызывает увеличение требуемых ресурсов и приводит к существенному увеличению длительности расчетов.
3. Исследование влияния шума на точность полученной модели
При увеличении значения шума ухудшается точность искомой модели, как показано на рис.2. Это приводит к увеличению количества шагов, необходимых для нахождения модели, и к существенному ее усложнению.
Не во всех случаях удалось найти модели с заданной точностью аппроксимации. Некоторые из искусственно сгенерированных зависимостей ![]() приняли вид, который трудно адекватно аппроксимировать квадратичным полиномом.
приняли вид, который трудно адекватно аппроксимировать квадратичным полиномом.
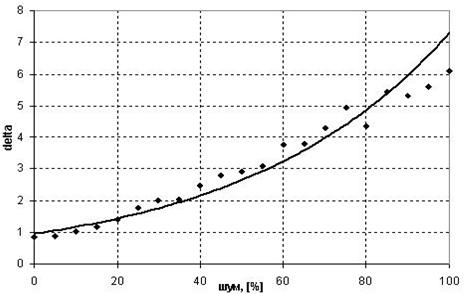
Рис. 2 Влияние уровня шума на точность полученной модели
4. Исследование влияния количества отбираемых наилучших частных описаний на каждом шаге
В плане выбора оптимального количества отбираемых на каждом шаге полиномов частных описаний однозначного ответа быть не может. Это обусловлено тем фактом, что с увеличением числа факторов существенно возрастает число их парных взаимодействий.
На практике прослеживается закономерность, что с увеличением числа отбираемых частных описаний на каждом шаге увеличивается точность полученной модели (рис.3). В свою очередь чрезмерное увеличение этого числа (m) приводит к большим объемам обрабатываемой информации.
Слишком же малое число отбираемых парных взаимодействий отрицательно сказывается на адекватности полученной модели.
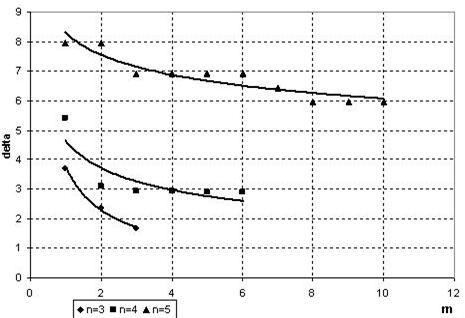
Рис. 3 Влияние числа отбираемых частных описаний на точность полученной модели для разных значений числа аргументов
Об оптимальном значении m можно говорить только в отношении конкретного n (числа исходных факторов). При решении конкретной задачи рекомендуется выполнить промежуточное исследование с использованием разработанного приложения для определения оптимального значения m.
5. Исследование влияния размеров подмножеств экспериментальных данных на точность искомой модели
В ходе исследования влияния размеров подмножеств О (обучающего), П (проверочного) и К (контрольного) исходной выборки данных были получены следующие результаты:
1) При равномерном разбиении выборки (О=П=К) точность модели прямо пропорциональна объему выборки (рис.4). Хотя чрезмерный объем данных может привести к существенному увеличению объема обрабатываемой информации.
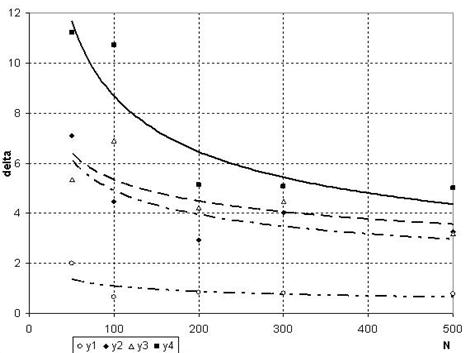
Рис. 4 Влияние размеров подмножеств экспериментальных данных на точность искомой модели при равномерном разбиении выборки (О=П=К)
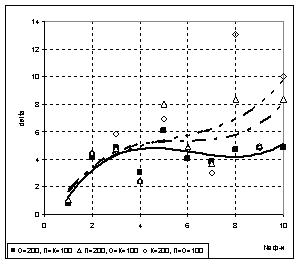
2) При неравномерном разбиении выборки было установлено, что увеличение обучающего подмножества по отношению к проверочному и контрольному (О=П+К, П=К) приводит к увеличению точности полученной модели по сравнению со случаем равномерного разбиения и разбиения в пользу П либо К, как показано на рис.5.
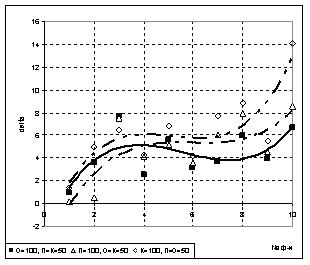
а) б)
Рис. 5 Влияние размеров подмножеств экспериментальных данных на точность искомой модели при неравномерном разбиении выборки:
а) N=200; б) N=400
3) При включении в состав К дополнительно подмножеств О либо П, либо О+П увеличивается точность полученной модели (изначально О=П=К). Наилучшая точность была получена при К=О+П (рис.6), т.е. вся выборка делится на две части: обучающее и проверочное подмножества. А выбор оптимальной модели происходит при этом по всей выборке (всему множеству экспериментальных данных). Следующее по точности разбиение К=О+П+К. Опять же при выборе модели учитывается вся выборка. Точность незначительно снижалась при разбиении К=П+К.
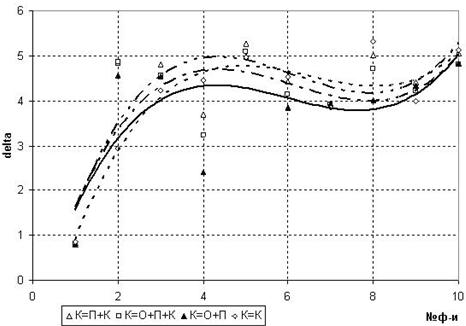
Рис. 6 Влияние включения в подмножество К дополнительных подмножеств экспериментальных данных на точность искомой модели (изначально О=П=К=200)
Дополнительное включение в контрольное подмножество подмножеств О и П повышает точность модели, поскольку в таком случае выбирается модель наиболее адекватная всей выборке. При стандартном разбиении (без включения подмножеств в состав К) есть риск, что на контрольном подмножестве функция, в целом не являющаяся наиболее точной моделью, будет иметь наименьшее среднеквадратическое отклонение от оригинала, что приведет к выбору модели не являющейся самой точной на всем исследуемом интервале экспериментальной выборки.
6. Влияние вида частных описаний на качество полученной модели
Изначально приложение реализовывало метод группового учета аргументов с функциями частных описаний квадратичного вида:
![]() . (10)
. (10)
В ходе исследований возник вопрос о влиянии вида полинома частных описаний на точность и сложность полученной модели.
Для сравнения были взяты функции частных описаний следующего вида:
![]() . (11)
. (11)
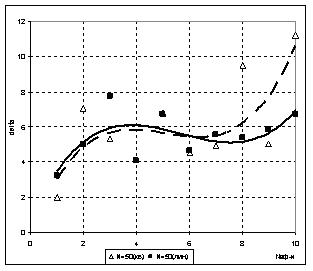
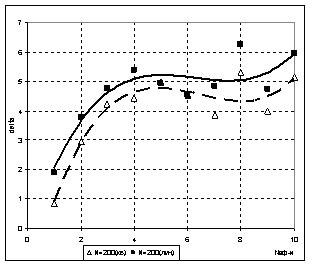
В ходе исследований было установлено, что такое упрощение вида функций частных описаний практически не сказалось на качестве полученной модели (наблюдалось незначительное снижение точности, как показано на рис.7). При этом происходит существенное упрощение вида искомой модели (даже при возможном увеличении количества шагов расчета) при практически неизменной точности модели. При n=3, m=3, e=0,75 модель объекта в обоих случаях была найдена за два шага расчетов, но если для варианта с частными описаниями вида (10) модель содержала 64 слагаемых, а точность (δ) составила 0.46, то для случая с частными описаниями вида (11) модель уже содержала 16 слагаемых и δ=0.70.
При некотором запасе точности использование упрощенного вида функций частных описаний может привести к существенному упрощению искомой модели.
Исследования проводились при следующих условиях: n=3...5, N1=N2=N3=50..500, m=2..15, B=10, A=0.25, Fi=100, Sh=0..20, e=0.1..5.
а) б)
Рис. 7 Влияние вида частных описаний на точность искомой модели:
а) N=50; б) N=200
Выводы
На сегодняшний день одним из универсальных экспериментальных методов идентификации многомерных систем есть метод группового учета аргументов. Вместе с тем метод имеет ряд особенностей, уточнение которых являлось основной задачей проведенной работы.
В статье представлена программная реализация МГУА, ориентированная на широкий спектр возможных применений – от решения исследовательских задач до решения прикладных задач построения модели объекта (вида “n входов – 1 выход”) по выборке экспериментальных данных. С помощью разработанного приложения возможно решение каждой конкретной задачи несколькими вариантами (при разных значениях параметров алгоритма) с целью получения модели объекта или системы оптимальной точности и сложности.
В ходе исследования практической (программной) реализации МГУА было установлено следующее:
1. С увеличением уровня шума и уменьшением числа отбираемых на каждом шаге частных описаний (m) ухудшается точность искомой модели, при этом возможно увеличение количества шагов, необходимых для нахождения модели, что может привести к существенному ее усложнению. При решении каждой конкретной задачи для определения оптимального значения m рекомендуется выполнить промежуточное исследование с использованием разработанного приложения.
2. При равномерном разбиении выборки (О=П=К) экспериментальных данных точность модели прямо пропорциональна объему выборки. При неравномерном разбиении выборки увеличение обучающего подмножества по отношению к проверочному и контрольному (О=П+К, П=К) приводит к увеличению точности полученной модели по сравнению со случаем равномерного разбиения и разбиения в пользу П либо К. При включении в состав К дополнительных подмножеств наилучшая точность была получена при К=О+П.
3. Вид частных описаний влияет на сложность полученной модели. Упрощение функций частных описаний от вида (10) к виду (11) приводит к упрощению модели, но при этом происходит незначительное ухудшение ее точности (при n=3, m=3, e=0,75 модель объекта в обоих случаях была найдена за два шага расчетов, но если для варианта с частными описаниями вида (10) модель содержала 64 слагаемых, а точность (δ) составила 0.46, то для случая с частными описаниями вида (11) модель уже содержала 16 слагаемых и δ=0.70).
При решении каждой отдельной задачи, для нахождения модели с оптимальными параметрами сложности и точности, рекомендуется поварьировать с использованием разработанного программного продукта такие параметры как число отбираемых частных описаний на каждом шаге и вид полинома частных описаний.
In the article the program application of the method of the group calculation of the arguments is represented. The following special features of method were investigated with the aid of the developed application: influence on the adequacy of the model of the level of noise, quantity of selected polynomials, dimensionality of task, sizes of subsets. The results of studies were represented.
1. Ивахненко А. Г. Долгосрочное прогнозирование и управление сложными системами. – Киев: Техніка, 1975.
2. Ивахненко А.Г. Индуктивные методы самоорганизации моделей сложных систем. – Киев: Наук. мысль, 1982.
3. Степашко В.С. Теоретические аспекты МГУА как метода индуктивного моделирования. – Труды I Международной конференции по индуктивному моделированию, Львов, 20-25 мая 2002 г.
4. Демидович Б.П., Марон И.А., Шувалова Э.З. Численные методы анализа. Приближение функций, дифференциальные и интегральные уравнения. – М.: Наука, 1967.
Ответы на вопросы [_Задать вопроос_]
Читайте также
Моделирование объектов и систем управления
Соколов А.Е., Махова Е.О. Моделирование процесса принятия педагогического решения при компьютеризированном обученииСлавко О.Г. Порівняльний аналіз керування регулятором на основі локальної моделі керованого процесу та П-регулятором
Войтенко В.В., Дикусар Е.В, Ситников В.С. Определение частоты среза устройства сглаживания данных на основе метода скользящего среднего
Передерій В.І. Алгоритм визначення та оцінки характеристик ефективності комп’ютерних систем на початковій стадії проектування в умовах невизначенності
Ляшенко С.А, Ляшенко А.С. Оценка модели псевдолинейной регрессии
Ладієва Л.Р. Математична модель процесу газової мембранної дистиляції
Носов П.С., Косенко Ю.І. Нечіткі моделі і методи ідентифікації та прогнозу стану інформаційної моделі студента
Китаев А.В., Глухова В.И. Анализ работы синхронного двигателя с неявнополюсным ротором по данным каталога
Дорошкевич В.К., Пироженко А.В., Хитько А.В., Хорольский П.Г. К определению требований к системам увода космических объектов
Голінко І.М., Ковриго Ю.М., Кубрак А.І. Настройка системи керування за імпульсною характеристикою об’єкта
Яшина К.В., Садовой А.В. Комплексная математическая модель тепловых процессов, происходящих в дуговых электросталеплавильных печах
Шейник С.П., Рудакова А.В. Использование функций принадлежности для моделирования параметров распределенных объектов
Хомченко А.Н., Литвиненко Е.И. Метод барицентрического усреднения граничных потенциалов электростатического поля
Селяков Е. Б. Моделирование требований к техническим системам методами математической логики
Тодорцев Ю.К., Ларіонова О.С., Бундюк А.М. Математична модель контура теплопостачання когенераційної енергетичної установки
Кириллов О.Л. , Якимчук Г.С. Моделирование процесса управления системой перегрузки углеводородных жидких топлив
Шеховцов А.Н., Козел В.Н. Построение математической модели формирования распределенных систем
Китаев А.В., Глухова В.И. Анализ поведения генератора постоянного тока по данным каталога
Хомченко А.Н., Козуб Н.О. Задачі наближення функцій: від лагранжевих до серендипових поліномів
Хобин В.А., Титлова О.А. Определение температуры парожидкостной смеси в дефлегматоре АДХМ по результатам измерений температуры его поверхности
Григорова Т.М., Усов А.В. Вероятностно-статистическое моделирование маршрутизированных пассажиропотоков в крупных городах
Горач О.О., Тернова Т.І. Моделювання технологічного процесу одержання трести при використані штучного зволоження з урахуванням складу мікрофлори
Дубік Р.М., Ладієва Л.Р. Математична модель розділення неоднорідних рідких систем
Казак В.М, Лейва Каналес Родриго, Яковицкая Е.Ю. Моделирование динамики полета магистрального самолета на исследовательском стенде
Завальнюк И.П. Исследование процесса торможения автомобиля как критического режима динамической системы
Дмитриев С.А., Попов А.В. Построение портрета неисправностей проточной части газотурбинного двигателя на примере АИ-25
Русанов С.А., Луняка К.В., Клюєв О.І., Глухов Г.М. Математичне моделювання робочого процесу в апаратах з віброкиплячим шаром та розробка систем автоматизованого моделювання гідродинаміки віброкиплячих шарів
Боярчук В.П., Сыс В.Б. Экспериментальные исследования влияния технологии шлихтования на изменение жесткости текстильных нитей
Селін Ю.М. Використовування контекстних марківських моделей для аналізу дії промислових вибухів на будівельні конструкції
Рудакова А.В. Проблемы интеграции сложных систем
Передерій В.І., Касап А.М. Математична модель та алгоритм автоматизації розрахунку параметрів комп’ютеризованих систем працюючих у реальному часі
Передерий В.И., Еременко А.П. Математические модели и алгоритмы принятия релевантных решений пользователями автоматизированных систем с учетом личностных и внешних факторов на базе генетических алгоритмов
Михайловская Т.В., Михалев А.И., Гуда А.И. Исследование правил клеточных автоматов для моделирования процессов затвердевания квазиравновесных бинарных сплавов
Хомченко А.Н., Колесникова Н.В. Явление «сверхсходимости» в задаче Прандтля для уравнения Пуассона
Китаев А.В., Глухова В.И. Анализ работы трансформатора по данным каталога
Квасницкий В.В., Ермолаев Г.В., Матвиенко М. В., Бугаенко Б.В., Квасницкий В.Ф. Оценка применимости метода компьютерного моделирования к исследованию напряженно-деформиррованного состояния цилиндрических узлов
Китаев А.И., Глухова В.И. Анализ работы асинхронного двигателя по данным каталога
Шелестов А.Ю Имитационная модель взаимодействия GRID-узлов с очередью доступа к общей памяти
Chizhenkova R.A. Mathematical Aspects of Bibliometrical Analysis of Neurophysiological Investigations of Action of Non-ionized Radiation (Medline-Internet)
Хомченко А.Н., Козуб Н.А. Геометрическое моделирование дискретных элементов с криволинейными границами
Славич В.П. Модель автоматизованої системи управління потоками транспортних засобів
Степанкова Г.А., Баклан І.В. Побудова гібридних моделей на основі прихованих марківських моделей та нейронних мереж
Бакшанська Т.Д., Рижиков Ю.Г., Тодорцев Ю.К. Математична модель процесу горіння природного газу з рециркуляцією продуктів згорання для цілей управління
Хомченко А.Н. Новые решения обобщенной задачи Бюффона
Передерий В.И., Еременко А.П. Математические модели и алгоритмы определения релевантности принимаемых решений с учетом психофункциональных характеристик пользователей при управлении автоматизированными динамическими системами
Ложечников В.Ф., Михайленко В.С., Максименко И.Н. Аналитическая много режимная математическая модель динамики газовоздушного тракта барабанного котла средней мощности
Ковриго Ю.М., Фоменко Б.В., Полищук И.А. Математическое моделирование систем автоматического регулирования с учетом ограничений на управление в пакете Matlab
Исаев Е.А., Наговский Д.А. Математическое описание влияния кривизны контактирующих тел на угол смачивания жидкости в межчастичном пространстве
Бідюк П.І., Литвиненко В.І., Кроптя А.В. Аналіз ефективності функціонування мережі Байєса
Тищенко И.А., Лубяный В.З. Математическое моделирование вокодера для определения оптимальной формы импульса сигнала возбуждения.
Николаенко Ю.И., Моисеенко С.В. Моделирование гармонического полиномиального базиса гексагона.
Козуб Н.А., Манойленко Е.С., Хомченко А.Н. Температурный тест для модифицированных базисов бикубической интерполяции.
Клименко А.К. Об упрощенном численном конструировании обратной модели динамического объекта.
Китаев А.В., Сушич Е.Ф. Расчет погрешностей измерительных трансформаторов.
Передерій В.І.,Касап А.М. Математична модель та алгоритм автоматизації розрахунку параметрів комп’ютеризованих систем працюючих у реальному часі
Шпильовий Л.В. Математична модель та алгоритм екстремального управління процесом осадження дисперсної фази суспензії.
Тулученко Г.Я. Інформаційний модуль експрес-пошуку точок еквівалентності процесу нейтралізації.
Тернова Т.І. Урахування морфогенетичного рівняння в математичній моделі тканини.
Попруга А.Г. Теоретические и экспериментальные исследования электрических нагревателей по критерию экономии энергии.
Китаев А.В., Сушич Е.Ф. Приложение положений теории дросселя и трансформатора к расчету и анализу электромагнитом переменного тока.