УДК    621.643.001.24

Развитие техники и технологии разведки и добычи энергоносителей со дна морей обусловило эффективность широкого освоения углеводородных ресурсов континентального шельфа. В экономической зоне акваторий Черного и Азовского морей обнаружено и прогнозировано 400 объектов нефтегазодобычи. Согласно программе “Освоения углеводородных ресурсов украинского сектора акваторий Черного и Азовского морей" добыча нефти до 2015 года может увеличиться до 3.2 млн. т. ежегодно [1]. Одним из важных предпосылок освоения нефтегазовых ресурсов шельфа является построение сети магистральных трубопроводов. Область применения способов укладки подводных трубопроводов может быть расширена с увеличением допустимой глубины путем применения специальных методов, что позволяет уменьшить изгибающие напряжения в трубопроводе. Для геологической разведки шельфа, обследования и ремонта трубопроводов широкое применение нашли привязные управляемые необитаемые спускаемые аппараты. Все эти длинномерные конструкции являются гибкими пространственно искривленными объектами, управление которыми, в частности их позиционирование при технологических процессах, имеет важное народно-хозяйственное значение. Анализ их напряженно-деформированного состояния необходим для выбора рациональной технологической схемы, разработки новых методов погружения трубопроводов на значительные глубины, создания принципиально новых управляемых глубоководных привязных систем.

Анализ последних исследований

Аналитические методы расчета гибких подводных объектов имеют давнюю историю. Наиболее широкое распространение получила методика, созданная С.И. Левиным [2]. Согнутый участок гибкого объекта рассматривается как балка на двух опорах. При этом учитывается, что в предельных точках (точка выхода на поверхность и точка касания дна) кривизна и угол поворота упругой оси по отношению к горизонтальной оси равно нолю. Предусматривается, что глубина погружения значительно меньшая, чем длина согнутой части гибкого элемента, которая принимается равной ее проекции на горизонтальную ось. П.Л. Терещенко [3] рассмотрел три характерных участка трубопровода: а) тот, что плавает; б) тот, что находится под водой и не касается дна; в) тот, что лежит на грунте. Наиболее значительный вклад в решение задач пространственного деформирования привязных спускаемых аппаратов и управления ими внес Магула В.Э. [4]. Им впервые в данной области предпринята попытка алгоритмизировать вычисления с помощью ЭВМ, однако использовались лишь аналитические методы вычислений. При математическом описании процесса погружения обычно составляют уравнение упругой линии для отдельных (двух или трех) участков гибкого объекта. При составлении и решении уравнений авторами делается ряд предположений, которые в определенной степени влияют на точность выведенных соотношений и решений. Решаемые задачи принадлежат, как правило, к плоскому случаю, не учитывается возможность пространственного деформирования вследствие действия внешних технических или естественных нагрузок. Прямое использование вектора внешних нагрузок, которое предлагается различными авторами, без критического анализа возможностей и области применения такого представления приводит в ряде случаев к неточным или даже неверным записям компонентов этого вектора. Классическим обобщением теории гибких стержней можно считать труды Попова и Светлицкого [5],[6]. Ими решены основные задачи, встречающиеся при расчетах напряженно-деформированного состояния, устойчивости и динамики гибких стержней. Однако, аналитические методы сейчас нельзя считать достаточно алгоритмичными, решение любой новой задачи требует больших усилий при математических вычислениях, временных затрат. Поэтому наиболее перспективным в данном направлении можно считать применение численных методов.

Формулировка целей

В процессе погружения подводных гибких объектов следует учитывать не только технические условия, но и механические нагрузки, которые возникают из-за влияния ветра, волнения моря, морских течений и маневров плавсредств. Сложные и тяжелые режимы эксплуатации гибких элементов сопряжены, как правило, с необходимостью специального изучения и определения действующих на них сил, учета сильной нелинейности разрешающих уравнений, возможности потери устойчивости равновесия и с требованием исследования поведения системы в закритических состояниях. Дифференциальные уравнения, описывающие их деформирование, имеют высокий порядок и содержат нелинейности сложного вида. Поиск их решения аналитически часто становится невозможным, что побуждает широко привлекать методы вычислительной математики. Решение таких задач оказывается возможным только современными методами нелинейного анализа, применение которых побуждает к выбору модификации разрешающих уравнений, обеспечивающих алгоритмичность и эффективность используемых подходов. До настоящего времени указанные исследования не получили необходимого развития из-за отсутствия достоверных математических моделей, которые достаточно просто и эффективно реализуются в виде алгоритмов и программ для численного решения рассматриваемых задач. Для описания влияния гидрометеосреды необходима адекватная пространственно-временная математическая модель изменения волнения, ветра и течения. Эта модель должна позволять воспроизводить реальные внешние условия как на коротких (секунды, минуты), так и на длинных (до года) интервалах времени с учетом вероятностной природы основных характеристик гидрометеосреды. Целью данной статьи является описание численного метода решения задачи управления гибким пространственно искривленным объектом при целенаправленных силовых воздействиях.

Методика исследования

В данной статье рассматривается математическая модель, основанная на известных подходах, описанных в [7]. В плане применения современных вычислительных алгоритмов она позволяет создать унифицированные методы исследования деформирования гибких подводных объектов, которые позволяют учитывать:

- неограниченность пространственного упругого деформирования;

- физико-геометрические параметры элементов с произвольными вдоль оси значениями изгибной и крутильной жесткостями;

- действие статических, квазистатических или динамических нагрузок, как угодно расположенных в пространстве;

- действие нагрузок от течения, волн, ветра, гидростатического давления.

Математическая модель базируется на известных подходах Лагранжа и Эйлера, которые описывают равновесие и деформирование гибкого элемента, его внешнюю и внутреннюю геометрию. Опишем кратко метод исследования.

Введем , ,  - естественный трехгранник с единичными ортами главной нормали и касательной;  - орты подвижного трехгранника;, - векторы внутренних усилий и моментов; p, q, r - кривизны относительно орт подвижного трехгранника; x, y, z – координаты независимой переменной s.

Представим систему разрешающих уравнений, которые описывают деформирование гибкого элемента, в виде

                                                                                       (1)

где           

                - вектор состояния (), f - вектор-функция правых частей системы уравнений; l - параметр интенсивности возмущения (нагружения), штрихом обозначена производная по s. Параметр l может быть как действительным, так и формальным, который отображает количественные характеристики задачи.

Сформулированная таким образом в области  изменения независимой переменной s система разрешающих уравнений (1) имеет общий восемнадцатый порядок. Наличие шести первых интегралов

                                                              (2)

позволяет уменьшить ее порядок до двенадцатого. Методика решения поставленной задачи основана на совместном использовании метода продолжения по параметру и метода Ньютона-Канторовича. На краю s = 0 интервала 0 s S изменения переменной s заданы шесть независимых краевых условий  и шесть вытекающих из первых интегралов уравнений связи . Для замыкания системы уравнений достаточно на краю s = S задать шесть независимых краевых условий . В сформулированных краевых уравнениях  обозначают шестимерные векторы-функции.

 Пусть при некотором значении  известно решение . Дадим малое приращение  параметра . Тогда соответствующую ему вариацию  решения  можно найти из линейного уравнения

                                                                   (3)

полученного линеаризацией системы разрешающих уравнений. Краевые уравнения для

функции  формируются линеаризацией начальных нелинейных краевых уравнений

 .                                                       (4)

Для построения  выберем среди составляющих  такие шесть компонент , любые значения которых  не изменяют первые два векторные уравнения системы (4). Перенумеруем неизвестные  так, чтобы индекс j принимал значения j =1,2,3,...6. Тогда решение задачи (4) представим в виде

                                                               (5)

где  - решение задачи Коши для системы

                                                                         (6)

при нулевых начальных условиях, Y(s) - матрица размера m6 решений системы

                                                                                         (7)

с начальными условиями  для независимых переменных, для других переменных -  Вектор постоянных  подбирается из уравнений

  .                                                        (8)

Выбирая состояние  как порождающее, вариацией параметра его можно продолжить на величину . Поскольку  найден с использованием линеаризованных уравнений, то решение  будет удовлетворять условиям поставленной задачи приблизительно с невязками. При практической реализации решения построение матриц Y(s) на каждом шаге варьирования параметра осуществляется методом Рунге-Кутта четвертого порядка. Количество шагов интегрирования и точек дискретизации по длине элемента зависит от многих факторов: глубины погружения, количества и характера, действующих по длине нагрузок, меры нелинейности процесса и тому подобное. Практическая реализация метода осуществлена в виде программ расчета на ЭВМ.

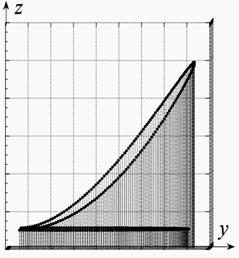
 Представленная методика численного расчета позволяет осуществлять управление гибкими протяженными объектами, заключающееся в следующем. Известно, что первоначально пространственно криволинейный объект сохраняет свою форму до тех пор, пока на него не воздействует какое-то силовое поле. Наиболее часто применяемые в настоящее время способы воздействия – это управление положением объекта с помощью гибких связей, принадлежащих одному, а чаще - нескольким судам-носителям. Такой метод является достаточно громоздким и дорогим, предъявляет большие требования к условиям гидрометеосреды. Более экономичным представляется метод управления гибкими объектами с помощью установленных на них устройствах, позволяющих за счет силовых воздействий на участки объекта приложением в различных сечениях нагрузок (сосредоточенных или моментных) изменять их положение по заранее предполагаемому закону. Для установления предполагаемой формы объекта необходимо заранее оперативно рассчитать его напряженно-деформированное состояние, после чего с помощью средств контроля уточнять его технологическое положение. Покажем процесс расчета на примере решения задачи пространственного деформирования первоначально плоского элемента под действием сосредоточенных и пространственно направленных нагрузок. Схема такого нагружения показана на рис. 1.

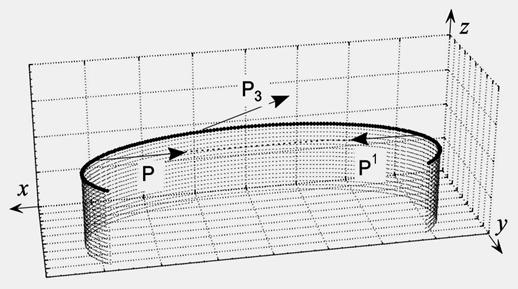
Рис.1 Внешний вид и схема нагружения гибкого элемента

Построение его геометрии осуществлено с помощью методики, описанной в [7], согласно которой исследуемый участок кривой является частью лемнискаты Бернулли. Следует подчеркнуть, что таким образом можно задавать геометрию кривой практически любой конфигурации. Здесь P=P¹ - сосредоточенные, равные и противоположно направленные силы, «стягивающие» два произвольно выбранных сечения элемента. Их действием достигается требуемое деформирование объекта в плоскости xy.

Сила P₃ осуществляет пространственное позиционирование из плоскости xy и направлена произвольно в пространстве, т.е. , где P_x = k_xP, P_y = k_yP, P_z = k_zP; k_x k_y k_z – коэффициенты пропорциональности, обозначающие распределение части исходного значения силы Р по ее составляющим.

Полученные результаты

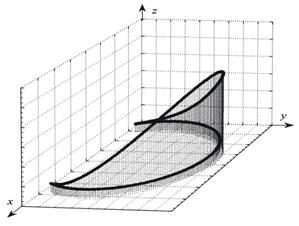
Будем считать, что в начальной стадии гибкий объект (гибкий трубопровод) находится в равновесии и сохраняет свою первоначальную форму. Вследствие приложения нагрузок P=P¹ он деформируется в плоскости, принимая форму продольной оси, значительно отличающуюся от первоначальной. После некоторой достигнутой формы для уточнения его пространственного положения прикладывается сила P₃. Для численного решения такой задачи по всей длине элемента задается 300 точек дискретизации. При этом проводится пошаговое интегрирование с дискретной нагрузкой Р - аналога параметра  (3). После определенного шага нагружения путем запоминания промежуточного решения прикладывается сила P₃ и далее решение продолжается при действии всех приложенных нагрузок. Результаты такого решения представлены на рис.2.

Следует отметить, что каждый шаг интегрирования отображается графически на экране дисплея, что позволяет визуально контролировать предполагаемое пространственное положение объекта и сравнивать его с действительным.

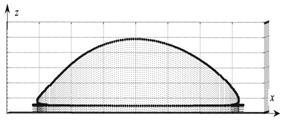
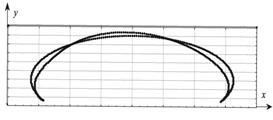
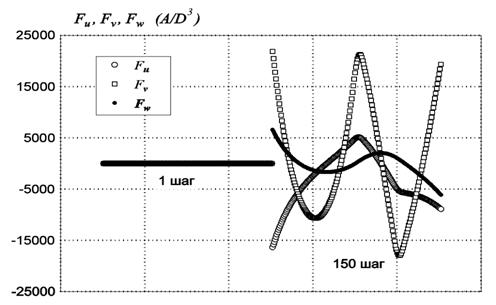
в)                                                                                         г)

Рис.2 Формы продольной оси деформированного гибкого элемента

в аксонометрическом изображении (а) и в проекциях на плоскости xz (б) , xy (в), yz (г)

Кроме того, в любой момент деформирования можно отобразить все внутренние силовые факторы на дисплее в виде таблиц или графиков (рис.3).

Результаты расчетов показывают эффективность представленной методики. Ее достоверность косвенно определяется сходимостью решений дифференциальных уравнений и кроме того отображена на естественности графического отображения результатов. Анализируя усилия, показанные на рис.3, можно сделать вывод о сильной нелинейности процесса. Таким же образом можно при необходимости изобразить графически и внутренние моменты в любом сечении на любом шаге. Приняв шаг интегрирования достаточно малым, можно осуществить контроль напряженно-деформированного состояния на всем этапе деформирования с необходимой дискретностью нагружения. Практика использования методики при решении тестовых задач показала, что для достаточной уверенности в достоверности получаемых результатов необходимо убедиться в сходимости интегрирования разрешающих уравнений. Одним из таких признаков является визуальное наблюдение с помощью компьютерной графики за геометрией объекта непосредственно в процессе решения на любом шаге интегрирования. Если по каким-то причинам (неправильно выбраны начальные условия, неправильно заданы нагрузки, неправильно выбрана величина шага нагрузки и тому подобное) задача численно не решается, то это, кроме программного контроля, сразу отображается на дисплее компьютера в виде нелогично расположенных геометрических форм объекта.

Рис.3 Внутренние усилия в сечениях гибкого элемента

в недеформированном состоянии (1-й шаг) и

в конце деформирования (150-й шаг)

Выводы

Применяя предложенную методику, можно без значительной перестройки вычислительных алгоритмов менять характер действия нагрузок, получать необходимые параметры напряженно-деформированного состояния гибких элементов. При некоторых реально возникших обстоятельствах (например, при приложении любой нагрузки, потере устойчивости, изменении жесткости вследствие аварии) возникает необходимость прекратить решение и после изменения определенных параметров задачи возобновить его опять, начиная с прерванного шага. Алгоритм разработанных подпрограмм предусматривает возможность изменения действия нагрузки на любом шаге числового интегрирования при помощи „запоминания" предыдущего шага, а также на любом интервале совокупности точек дискретизации. Простота использования, наглядность, скорость получения результатов делают методику удобной для использования инженерами при расчетах и технологических работах.

1.                   Коростель г. П., Крупский Б.Л., Гладун В.В. Дальнейшие поисково-разведывательные работы на нефть и газ в акваториях Черного и Азовского морей (украинский сектор) // Нафт. и газовая промышленность. 2001. - №4. с. 6-9.

2.                   Левин С.И. Проектирование и строительство подводных трубопроводов. - М.: Гостоптехиздат, 1960. - 63 с.

3.                   Терещенко П.П. Укладка подводных трубопроводов способом свободного погружения. - М.: Недра, 1965. - 67 с.

4.                   Магула В.Э. Блинцов В.С. Проектирование самоходных привязных подводных систем. - Киев: Наукова думка, 1997. - 139 с.

5.                   Попов Е.П. Нелинейные задачи статики тонких стержней. - М.: ОГИЗ, 1948. - 178 с.

6.                   Светлицкий В.А. Механика трубопроводов и шлангов: Задачи взаимодействия стержней с потоком жидкости или воздуха. - М.: Машиностроение, 1982. - 279 с.

7.                   Кравцов В.И. Механика гибких морских конструкций. Киев: Наукова думка, 1999. – 132с.