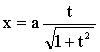УДК621.01
СИНТЕЗ СТРОФОЇДОГРАФІВ
ЗА МЕТОДОМ ПАРАМЕТРИЧНИХ СІМЕЙ
Бергер Е.Г., Дмитрієв Д.О., Бергер Є.Е., Діневич Г.Ю.
Механізми для відтворення заданої кривої знаходять широке розповсюдження в пристроях для обробки криволінійних поверхонь, вузлах машин-автоматів, маніпуляторах промислових роботів тощо [1, 2]. Їх синтез базується на принципі механічної реалізації графічних побудов даної траєкторії: схема побудов розглядається як геометричний аналог кінематичної схеми механізму. Для знаходження способу (схеми) побудов скористаємось методом [3], за яким крива F, задана рівнянням
|
F (x, y)=0, |
(1) |
визначається як геометричне місце точок перетину відповідних[1] кривих α і β, що належать однопараметричним сім'ям кривих
|
α (x, y, t)=0.....(α); β (x, y, t)=0.....(β), |
(2) |
при умові, що виключення параметра t з (α) і (β) призводить до (1).
Як особливий випадок можна навести широко відомий в математиці приклад представлення кривої F параметричними рівняннями
|
х=α ( t ).....(α); y=β ( t ).....(β), |
(3) |
де (α) і (β) – однопараметричні сім’ї прямих ліній, паралельних осям координат.
Точки перетину відповідних ліній сімей (2) або (3), побудованих при конкретному значенні t=ti , належать до кривої F. Змінюючи t , одержуємо множину точок кривої F.
Розглянемо застосування цього методу на прикладах синтезу механізмів для відтворення кривої 3-го порядку F
|
|
(4) |
відомою під назвою строфоїда.
Перше рівняння (α) вибираємо довільно в вигляді y=(a+x)t; підставивши це в (4), одержуємо
|
y=(a+x)t....
(α1); |
(5) |
При цьому очевидно, що виключення параметру t з (α1) і (β1) призводить до рівняння (4).
Прийнявши за параметр t зміну величину t=tgφ, маємо
|
y= tgφ(a+x)....(α1') ; x= a∙sinφ....(β 1'). |
(5') |
При змінному параметрі φ рівняння (α1') виражає пучок прямих СМі (рис.1а) з вершиною С(-а,0); tgφ – змінний кутовий коефіцієнт цих прямих, а рівняння (β 1') – сім’ю прямих АіМі║Оу, які проводяться на відстані ONi = a∙sinφi. Звідси випливають наступні способи побудов заданої кривої F (довільних її точок Мі):
1) Рис.1а. З точки С(-а,О) проводимо довільний промінь СМі пучка (α1') і перпендикулярно до нього пряму ОВАі . Якщо відкласти ОАі = а, то пряма АіМі║Оу буде належати до сім’ї (β 1'). Дійсно, легко бачити, що ONi = a∙sinφi , значить точка Мі перетину СМі і АіМі належить строфоїді (4); змінюючи φ, будемо одержувати множину її точок.
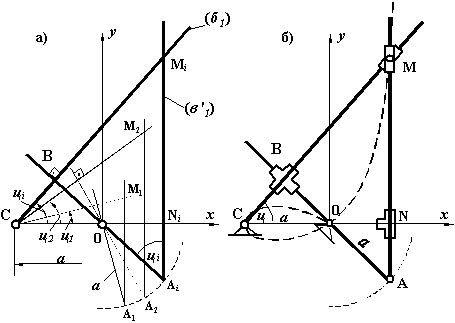
Рис.1
Механічна реалізація цих побудов – заміна геометричних елементів їх механічними представниками (точки С, О, А – шарніри, В, N – повзуни, М – шарнірно зв’язані повзуни, прямі ОВА, АМ і СМ – кривошип, лінійка і куліса відповідно) дає кінематичну схему строфоїдографа за рис.1б.
2) Рис.2а. Під довільним кутом φ проводимо промінь СМ пучка (α1') і паралельно йому на відстані а – пряму l-l, яка перетинає Оу в точці А. Перпендикуляр з А на СМ – визначає точку М, яка є точкою строфоїди. Дійсно, з рис.2а маємо КМ= a∙sinφi., тобто пряма NМ║Оу належить до сім’ї (β 1'). Реалізація цих побудов виконується строфоїдографом, що подано на рис.2а. Модифікацією цього механізма (повзун М перенесено до шарніру С) є відомий механізм Неуберга-Лебо [1] – рис.2б.
Приймаємо далі рівняння першої сім’ї в вигляді y=t∙x... (α2); з сумісного вирішення (α2) і (4) рівняння другої сім’ї може бути подане в різних формах, наприклад:
|
y=t·x .... (α2); |
|
(6) |
|
y=t·x .... (α2); |
|
|
|
y=t·x .... (α2); |
|

Рис.2
При t=tgφ рівняння (α2) виражає пучок прямих з вершиною О (на рис. 3, 4 показано один промінь ОА цього пучка з довільним кутом φ; промінь ОА має змінний кутовий коефіцієнт t=tgφ), а кожне з рівнянь (β 2.і) відповідно подає:
- (β 2.1) – сім’я прямих, які проходять через змінну точку N з координатами N(-а, a∙tgφ) перпендикулярно до променя ОА (кутовий коефіцієнт дорівнює -1/tgφ) – рис.3.


Рис.3
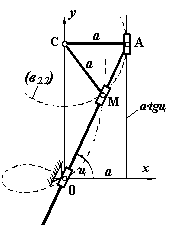
Рис.4
Перетин прямої NМ з променем ОА визначає точку М, яка належить строфоїді (рівняння 4). На рис.3а,б показано два способи побудов (відрізняються способом визначення точки N, тобто відкладання відрізка КN=a∙tgφ), реалізація яких виконується строфоїдографами Артоболевського [1].
— (β 2.2) – сім’я кіл постійного радіусу r=a із змінним центром С(О, a∙tgφ) – рис.4. Точка перетину кола з промінем ОА належить строфоїді (Бергер Е.Г. Авт.св.№190591, 1965 р.)
— (β 2.3) – сім’я прямих DM, що проводяться паралельно Оу на змінній відстані ОN, яка при довільному φ визначається за формулою ОN=х(1- tg2φ): (1+ tg2φ)=-а∙cos2φ; Таким чином, побудова потребує відкладення подвійного кута 2φ, значить до складу механізма повинен входити пристрій для подвоєння кута, наприклад, редуктор - рис.5 (Бергер Е.Г. Авт. св. №193735, 1967 р.).
Подвоєння кута можна виконувати також за допомогою ромбоїда OCBD (рис.6а); використання ромбоїда (замість редуктора) призводить до відповідної конструкції строфоїдографа за рис.6а (Бергер Е.Г., Табацков В.П., Діневич Г.Ю. Авт. св. №772898, 1980 р.).
Зауважимо, що в даному строфоїдографі фігура BCМD зберігає симетричність відносно діагоналі ВМ (значить і прямокутність кутів D і С) при будь-якому положенні механізма.
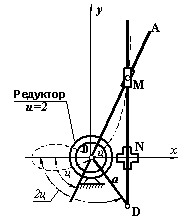
Рис.5
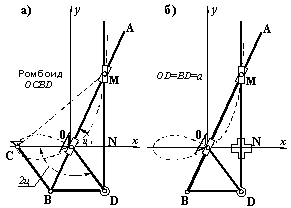
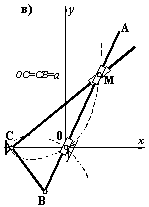
Рис.6
Звідси випливають дві модифікації цієї конструкції, наведені на рис.6 б,в. Першу одержано зміною ланки СВ на хрестовий повзун N, який забезпечує плоскопаралельне переміщення важеля ВМD (Бергер Е.Г. та ін. Авт. св. №628007, 1978 р.) – рис.6б. Другу схему одержано введенням замість важелю ВDМ прямокутного важеля ВСМ шарнірно встановленого у вершині С – рис.6в.
Як показують наведені приклади, розглянутий метод є досить ефективним засобом визначення схеми графічних побудов заданої кривої. такі задачі широко застосовуються в математиці (графіки функцій), в механиці (траєкторії руху тіл) і в теорії машин і механізмів (синтез напрямних механізмів).
В поєднанні з принципом механічної реалізації графічних побудов метод дає можливість одержувати різні кінематичні схеми напрямних механізмів, що дозволяє вибирати оптимальну за даними умовами роботи конструкцію.
При використанні високопродуктивних програм MATLAB, Maple та ін. геометрична модель метода, яка наведена в [3], дозволяє виконувати обчислення, візуалізацію та програмування в зручному середовищі для проектувальника [4].
Таким чином, метод відкриває додаткові перспективи в проектуванні напрямних механізмів як засобів автоматизації виробничих процесів.
It is presented the method of one-parametrical families and on this basis the synthesis of directing mechanisms (strophoid's graphs) is carry out.
1. Артоболевский И.И. Теория механизмов для воспроизведения плоских кривых.-М.АНСССР, 1959.-255с.
2. Бергер Э.Г., Табацков В.П., Бергер Е.Э. Геометрия формообразования криволинейных профилей. //Вестник ХГТУ, №3(9), Херсон, 2000.-С.224-226.
3. БергерЭ.Г., Литвиненко Е.Н., Гучек П.Н. Геометрическая модель обобщенного метода образования кривых. // Сб. Математическое моделирование в образовании, науке и промышленности. С.-Пб., 2000. –с.31-34.
4. Потемкин В.В. Matlab 5.x Система инженерных и научных расчетов. М. Диалог, МИФИ. 1999.- 670с.
Ответы на вопросы [_Задать вопроос_]
Читайте также
Современные технические средства, комплексы и системы
Краснов В.А., Прохорович А.В., Шутов С.В., Деменский А.Н. Анализ флуктуаций размера растущего кристалла (на примере легированных монокристаллов кремния, вытягиваемых из расплава по методу Чохральского)Завальнюк И.П. Управление высокопроизводительной экструзией неоднородных материалов
Долина В.Г., Писаренко А.В. Синтез складної багатовимірної системи управління випарною станцією на основі рефрактометричних вимірювань
Стопакевич А.А., Тодорцев Ю.К. Анализ современного состояния систем управления брагоректификационными установками спиртового производства
Поливода В.В. Современные компьютерные технологии в АСУ на хлебоприёмном предприятии
Ладанюк А.П., Українець А.І., Кишенько В.Д. Управління автоматизованими технологічними комплексами харчових виробництв на основі сценарного підходу
Ковриго Ю.М., Фоменко Б.В. Врахування обмежень для підвищення якості функціонування систем регулювання енергоблоків ТЕС і АЕС
Евдокимов А.В., Китаев А.В., Агбомассу В.Л. Исследование причин, определяющих вращение рамки с током в магнитном поле после воздействия на нее внешнего импульса
Аппазов Э.С. Применение твердых растворов InGaN в фотовольтаике
Кузнєцов Ю.М., Дмитрієв Д.О. Програмно математичний апарат керування виконавчим органом багатокоординатних верстатів нових компоновок
Черевко О.И., Ефремов Ю.И., Одарченко А.М., Одарченко Д.М, Агафонова Ю.Ю. Теоретическое обоснование перспективного биконического резонатора для СВЧ-устройств при переработке растительного сырья
Хобин В.А. Бабиков А.Ю. Системы экстремального управления молотковыми дробилками с функцией гарантированного соблюдения тепловых режимов их электродвигателей.
Стадниченко В.Н. Исследование влияния изменения эксплуатационных нагрузок на свойства металлокерамических слоёв полученных с использованием трибовосстанавливающих составов
Ісаєв Е.А., Наговський Д.А., Чернецька І.Е. До вибору факторів, що характеризують окомкування тонкоподрібнених залізорудних матеріалів
Федоровский К.Ю., Лунев А.А. Теплоотдача погружного пластинчатого теплообменника системы охлаждения энергоустановок морских технических средств
Федоровский К.Ю., Владецкий Д.О. Интенсификация теплоотвода замкнутых систем охлаждения энергоустановок морских технических средств.
Пономарьов Я.Ю., Ладанюк А.П., Іващук В.В. Досвід використання нечітких регуляторів в системі атоматизації випарної установки.
Левченко А.А., Кравчук О.И. Эквивалентный макромодуль процесса технического обслуживания радиотехнических средств.
Іволгіна Т.О. Енергетичний підхід до аналізу стійкості руху вимірювальної головки координатно-вимірювальної машини
Ладанюк А.П., Кишенько В.Д., Ладанюк О.А. Системна задача управління біотехнологічними процесами.
Тернова Т.І. Алгоритм оцінювання деформацій рапорту періодичних об'єктів
Рожков С.А., Федотова О.Н. Алгоритм обучения системы распознавания автоматической системы разбраковки тканей
Пупена О.М, Ельперін І.В, Ладанюк А.П. Особливості проектування комп’ютерно-інтегрованих систем управління
Квасніков В.П., Кочеткова О.В. Проектування координатно–вимірювальної машини на нейронних мережах
Водічев В.А., Мухаммед М.А. Дослідження системи стабілізації потужності різання металообробного верстата з фази-регулятором
Шутов С.В., Аппазов Э.С., Марончук А.И., Самойлов Н.А. Методика испытания термофотовольтаических преобразователей
Хобин В.А. Повышение качества формирования смесей средствами интеллектуализации алгоритмов управления порционным дозированием
Терновая Т.И. Автоматическая система разбраковки тканей с печатным рисунком методом компенсации информационных потоков
Рожков С.А., Бражник Д.А. Использование нейросетевых структур для построения систем распознавания образов
Місюра М.Д., Кишенько В.Д. Математичні моделі технологічних процесів пивоварного виробництва як об’єктів автоматизації
Ладанюк А.П., Власенко Л.О. Автоматизоване управління бізнес-процесами в комп’ютерно-інтегрованих структурах підприємства
Жукова Н.В., Литвинов В.І. Вирішення проблеми погодженого руху валків з неоднаковими катаючими діаметрами профілезгинальних станів
Денисова А.Е., Тодорцев Ю.К., Максименко И.Н. К вопросу об автоматизации интегрированной установки теплоснабжения с возобновляемыми источниками энергии
Бессараб В.И. Компьютеризированная система управления водоотливным хозяйством угольных шахт по критерию минимума энергозатрат
Хобин В.А. Регулятор переменной структуры для объектов технологического типа
Тонконогий В.М. Трехконтурная АСУ нанесением ионно-плазменного покрытия на режущий инструмент.
Колесникова Е.В., Кострова Г.В. Формирование базы данных АСУТП дуговой сталеплавильной печи.
Водічев В.А. Автоматизована система керування швидкостями робочих рухів то-карного верстата для підвищення ефективності обробки торцевих поверхонь.
Бабак В.П., В.Н. Стадніченко, О.Г. Приймаков Прогнозування надійності, дов-говічності та витривалості авіаційних матеріалів
Бабак В.П., Стадниченко В.Н., Приймаков О.Г., Токарчук В.В. Прогнозування витривалості авіаційних матеріалів .
Куцак Р.С. Використання методу координатного еталону в задачах автоматизації контролю якості тканини.
Попруга А.Г. Усовершенствование электрических нагревателей по критерию экономии энергии.
Пашковский А.А., Далечин А.Ю. Система регистрации спектров фотолюминес-ценции
Никольский В.В., Цюпко Ю.М. Применение пьезоэлектрических датчиков в сис-теме кондиционирования воздуха судовых систем микроклимата.
Крапивко Г.И., Хлопёнова И.А. Повышение коэффициента полезного действия кремниевых фотоэлектронных преобразователей методом лазерной гравировки.
Кихтенко Д.А. Управление шаговыми двигателями в микрошаговом режиме, оп-тимизация управления.
Горохов В.А. Автоматизированная транспортно-складская система в текстильной и легкой промышленности.
Водічев В.А. Система стабілізації потужності різання фрезерного верстата з взаємозв'язаним керуванням швидкостями робочих рухів.
Шутов С.В., Аппазов Э.С., Марончук А.И. Испытание фотоэлектрических преобразователей в условиях экстремальных температурных колебаний.
Худяев А.А. К проблеме повышения точности воспроизведенияв классе многоканальных воспроизводящих систем с эталонной настройкой каналов.
Тверезовський В.С., Бараненко Р.В. Принцип побудови елементів вимірювальних систем, представлених цифровими програмно керованими давачами.
Никольский В.В., Сандлер А.К. Моделирование процессов в вискозиметре с пьезоэлектрическим приводом.
Марончук И.Е., Андронова Е.В., Баганов Е.А., Курак В.В. Использование метода импульсного охлаждения насыщенного раствора-расплава для формирования наноразмерных структур InSb в матрице GaSb.
Водічев В.А. Аналого-цифровий регулятор режиму металообробки для верстатів з числовим програмним керуванням.
Блинов Э.И., Кравцов В.И., Кравцов А.В., Недбайло А.Н. Управление гибкими протяженными объектами направленными силовыми воздействиями.