Автоматика.
    Автоматизация.
        Электротехнические
            комплексы и системы.

УДК 681.5.012: 681.513.3

К ПРОБЛЕМЕ ПОВЫШЕНИЯ ТОЧНОСТИ ВОСПРОИЗВЕДЕНИЯ

В КЛАССЕ МНОГОКАНАЛЬНЫХ ВОСПРОИЗВОДЯЩИХ

СИСТЕМ С ЭТАЛОННОЙ НАСТРОЙКОЙ КАНАЛОВ

Худяев А.А.

В настоящее время ко многим системам автоматического управления, в том числе к воспроизводящим системам, предъявляются все более высокие требования в отношении полосы пропускаемых частот, порядка астатизма, установившейся динамической точности, максимального ускорения и других динамических показателей.

Воспроизводящие системы, обладающие высокой динамической точностью, необходимы для управления современными быстропротекающими производственными процессами, а также для создания разного рода информационно-измерительных и контролирующих устройств. Известно, что возможности системы в отношении динамической точности в конечном счете определяются предельными значениями координат и производных координат, характеризующих поведение входящих в систему элементов. В первую очередь важны ограничения, наложенные на скорости и ускорения, а иногда, и на рывки привода системы. В одноканальных САУ эти ограничения часто не позволяют увеличивать динамическую точность системы и полосу пропускаемых ею частот до требуемых значений.

Для повышения точности воспроизведения полезного сигнала могут быть использованы многоканальные системы, работающие по замкнутому и разомкнутому циклам [1]. Последующее развитие таких систем привело к созданию многоканальных систем, построенных по принципу “грубого” и “точного” управления и получивших название итерационных многоканальных систем [2]. В классе итерационных многоканальных систем воспроизведение задающих воздействий осуществляется последовательными приближениями (итерациями), реализуемыми соответствующими каналами управления [2,3]. Это позволяет потенциально обеспечить максимально высокую заданную точность работы всей многоканальной системы при стандартных (эталонных) настройках отдельных каналов и в большинстве случаев получать качество воспроизведения, недостижимое в одноканальных системах управления [4 - 6].

В настоящей статье рассмотрим принципиальную возможность эффективного решения проблемы повышения точности воспроизведения полезного сигнала при наличии аддитивных возмущений в подклассе неравноточных многоканальных систем с эталонной настройкой каналов, взаимодействующих по итерационному алгоритму. В частности, решим задачу удобного формального описания неравноточного итерационного алгоритма функционирования многоканальных САУ при наличии помех.

Неравноточный итерационный алгоритм построения многоканальных систем

Практическое применение при создании итерационных систем управления получили так называемые неравноточные итерационные алгоритмы построения [7–9], благодаря сравнительной простоте их технической реализации. В таких системах каждый последующий i-й канал вносит поправку y в сформированное предшествующими (і-1)-им каналами текущее значение y воспроизводимого сигнала, повышая эффективность системы по і-му выходу. При этом процесс воспроизведения итерационной N-канальной линейной системой полезного сигнала  с учетом влияния аддитивных помех в каналах может быть описан рекуррентными соотношениями вида

y(t)=y(t)+ (t),                                                               (1)

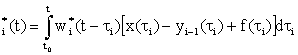
y ,                        (2)

где y - i-ое приближение к , y;  - сигнал на выходе N-канальной системы; y - поправка, вносимая на i-ом этапе итераций;  - функция веса i-го замкнутого канала; f - помеха (шум), приведенная ко входу i-го автономного канала. Из (1), (2) для ошибок  (i=) воспроизведения  в установившемся режиме () получим:

,

             .                 (3)

В частности, при i=N ошибка N-канальной системы

,                                                               (4)

где e (i=) – функция веса ошибки i-го автономного канала,  – -функция Дирака.

Динамику многомерных, в том числе итерационных многоканальных, систем удобно описывать в векторно-матричной форме, используя операторные представления. На основании соотношений связи (1) – (4) получим следующие операторные уравнения, описывающие динамику неравноточной итерационной N-канальной системы:

 =M,                                                      (5)

=  E-M, pd/dt,                              (6)

где

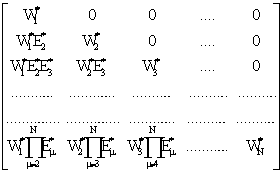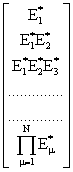 M=M=; E=.                   (7)

Здесь pd/dt – оператор дифференцирования по времени; ММ –операторная матрица, преобразующая в общем случае вектор входа системы = с элементами   в вектор выхода = и определяемая на основании (1), (2); ЕЕ и ММ – операторные матрицы, преобразующие соответственно сам полезный сигнал  и вектор помех =[] в векторы ошибок многоканальной системы:

и

,

и определяемые на основании (3), (4). В матрицах (7) обозначено:  () – линейные дифференциальные операторы отдельных каналов, соответствующие функциям ; ЕЕ ()- операторы ошибок отдельных каналов, соответствующие е.

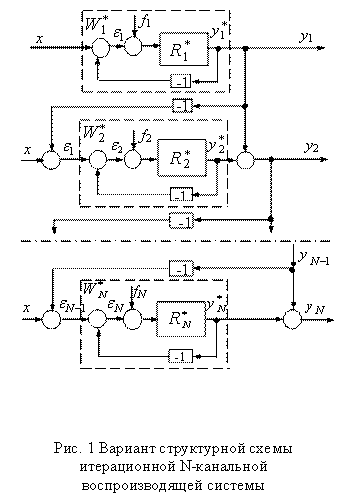
Полученным операторным матрицам М и Еудовлетворяют соответствующие им структуры неравноточных итерационных САУ [2,7,9]. Вариант структурной схемы  неравноточной итерационной N-канальной воспроизводящей системы, предназначенной для измерения полезного сигнала, показан на рис.1, где R () – операторы отдельных разомкнутых каналов.

Из формул (3) - (7) и рис.1 видно, что в неравноточных итерационных многоканальных системах, в отличие от равноточных [7], ошибки  уменьшаются с ростом номера i=1,2,…,N канала воспроизведения. При этом точность воспроизведения задающего воздействия  N-канальной (N2) системой может быть существенно повышена по сравнению с одноканальной (N=1) за счет подключения дополнительных уточняющих каналов.

Формирующие параметры каналов

Преимущественное применение в промышленных автоматизированных электромеханических системах получили системы управления унифицированными электроприводами с эталонной (или типовой) настройкой контуров управления и с возможностью перенастройки основных параметров регуляторов. Для синтеза таких систем используют метод эталонных операторов (ЭО), развитый применительно к итерационным многоканальным САУ в работах [2,5,10]. Согласно этому методу динамика процессов в каждом автономном канале многоканальной системы определяется некоторым выбранным эталонным оператором W (). При этом реальные операторы каналов W, соответствующие , представляются в виде:

W= W ,                                       (8)

где r- формирующий параметр (масштабный множитель), имеющий размерность времени; в этом случае  характеризует полосу пропускания соответствующего i-го канала с эталонной настройкой;

W,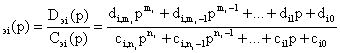

                                                     (9)

заданные (или синтезированные) эталонные операторы, соответствующие принятым

типовым настройкам каналов.

Из (8), (9) следует, что с физической точки зрения каждый формирующий параметр r () определяет реальную полосу пропускания  соответствующего i–го канала с эталонной настройкой, не меняя при этом характера динамики заданных (эталонных) характеристик, в частности, частотной характеристики канала W, где  - угловая частота (скорость), рад/с. Поэтому, не нарушая общности, примем: r .

Учитывая, что воспроизводящие системы обладают астатизмом, как правило, не ниже первого порядка, то есть в формуле (9) с , для операторов ошибок каналов многоканальной воспроизводящей системы с учетом (8), (9) можно записать

Е, ;

Е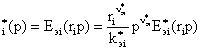 ,                                           (10)

где ≥1 и  - порядок астатизма и коэффициент усиления i–го канала. Из (10) для коэффициента ошибки , характеризующего величину сигнала ошибки  

N-канальной системы с эталонной настройкой, получим:

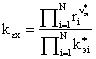.                                                         (11)

Отсюда видно, что при обращении в нуль любого из масштабных множителей r (), что соответствует бесконечной полосе пропускания этого канала, имеет место полная инвариантность итерационной системы по отношению к полезному сигналу .

Значения формирующих параметров r () характеризуют также соотношения между полосами пропускания отдельных каналов. Если оператор первого канала принят в качестве эталонного  (r=1), то числа , ,…,  показывают, во сколько раз полоса пропускания k-го  канала  шире (если < 1 ) полосы пропускания первого . Как видно из (11), с увеличением полосы пропускания (<1) уменьшается значение коэффициента ошибки  и увеличивается компенсирующее действие k-го (k=) канала по сигналу ошибки .

В качестве эталонной системы, получившей широкое применение при синтезе воспроизводящих САУ, примем фильтр Боттерворта -го порядка [2], для которого с учетом (9)

W,                                            (12)

где характеристический полином С в зависимости от порядка (≤) имеет вид:

 С=+1,                                                         (13)

 С=,                                                 (14)

С=.

Фильтр Боттерворта, как известно, имеет частотные характеристики компактно расположенные относительно частоты = и является приближением к идеальному ФНЧ.

Таким образом, динамика i-го канала, описываемая заданным эталонным оператором (9), соответствует принятой типовой настройке канала и зависит от одного формирующего параметра , определяющего полосу пропускания этого канала. При этом метод ЭО позволяет определить влияние каждого из каналов с заданной эталонной настройкой  (i=) на динамические свойства N-канальной системы с помощью минимального числа формирующих параметров ,,…,, равного числу каналов. В результате сложная задача синтеза оптимальных операторов N-канальной итерационной системы сводится к более простой задаче параметрической оптимизации в области формирующих параметров. Вопросы анализа и синтеза собственно итерационных многоканальных систем, в том числе с эталонной настройкой каналов, рассмотрены, в частности, в работах [5,6,10,11].

Ошибки и структуры неравноточной итерационной двухканальной (N=2) воспроизводящей системы

Из-за относительно высокой стоимости технической реализации, производства и эксплуатации реальных многоканальных систем, построенных по итерационному принципу, преимущественное применение для повышения точности воспроизведения законов управления получили, прежде всего, двухканальные (N=2) итерационные системы с эталонной настройкой [4,8,9,12,13]. Соотношения (3) - (9) позволяют исследовать влияние динамических характеристик каждого из каналов на динамические свойства двухканальной системы.

Ошибку воспроизведения неравноточной итерационной двухканальной системой получим из формул (6), (7) при N=2:

 ,                                           (15)

где                                                                                                                                                           

,                                                  (16)

 ,                                           (17)

                                                    (18)

- составляющие установившегося значения ошибки системы соответственно по задающему воздействию  и от действия помех  на первый и  на второй каналы.

Ошибку одноканальной (грубой) системы найдем, полагая в (15) ; :

,                             (19)

где

,                                                 (20)

                                                (21)

-                     составляющие установившегося значения ошибки первого, грубого канала двухканальной системы соответственно по задающему воздействию  и помехе . Тогда вместо (15) для двухканальной системы получим

,

откуда с учетом (16) – (18) видно, что при , то есть при достаточно широкополосном втором, точном канале:

, ()  ().

Из приведенных соотношений следует, что в неравноточной итерационной двухканальной системе на выходе второго, точного канала имеет место одновременная компенсация ошибок, обусловленных как задающим воздействием , так и помехой , приложенной к первому, грубому каналу. Помеха , приложенная ко второму каналу, не компенсируется. В этом смысле каналы не равноценны.

В подклассе итерационных двухканальных систем [2-4,6,8,9] первый, грубый канал W (см. рис.1 при N=2) несет на себе основную силовую нагрузку в реализации задачи воспроизведения  () и обладает необходимым усилением по мощности. Второй, точный канал W – маломощный, но имеет, как правило, значительно более широкую полосу пропускания  (>) и относительно невысокий уровень помех . Задача второго канала – компенсация сигнала ошибки  (19) воспроизведения  первым, грубым каналом W, для чего он должен иметь высококачественное (например, цифровое) измерительное устройство. С учетом этого первый канал принято также называть основным, а второй – компенсирующим.

В итерационных двухканальных измерительных системах выходная величина  формируется по разомкнутому циклу, что предъявляет высокие требования к точности суммирования  и . Структуры итерационных измерительных систем, рассмотренные в работах [6,10,11] и на рис. 1, неприменимы, если выход системы связан с силовой нагрузкой.

Варианты структурных схем итерационных двухканальных воспроизводящих систем с контролем выходной величины y по замкнутому циклу показаны на рис. 2,а,б, где  (i=1,2) - операторы отдельных разомкнутых каналов. Эти структуры также реализуют неравноточный итерационный алгоритм воспроизведения (1) - (7) при N=2 . Однако, в отличие от структуры на рис. 1, структуры на рис. 2 соответствуют итерационным системам, выход которых связан с инерционной (силовой) нагрузкой.

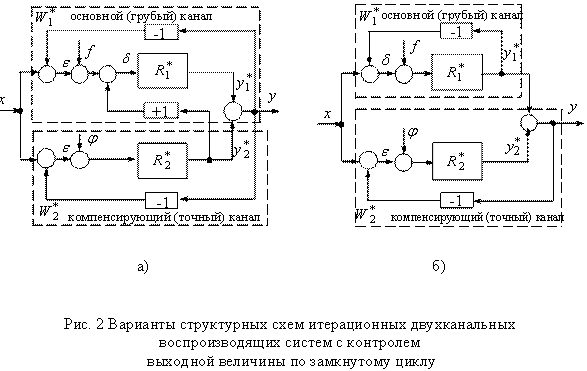
Выводы

1.                  Показано, что при 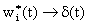 на i-ом выходе итерационной многоканальной системы эквивалентный полезный сигнал воспроизводится практически без искажений, то есть достигается компенсация не только динамических ошибок воспроизведения задающего воздействия 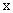(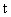), но и ошибок от воздействия помех 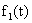, ,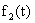…,  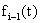на предшествующие каналы. Наличие помехи 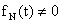 в последнем уточняющем канале (i=N) ограничивает достижение максимально высокой точности воспроизведения с помощью неравноточных итерационных систем, так как ошибка, обусловленная 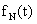, остается нескомпенсированной. Вместе с тем, интенсивность помехи 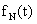, как правило, весьма незначительна.

2.                  Получена удобная векторно-матричная форма (5) - (7) формального описания неравноточного итерационного алгоритма функционирования многоканальных САУ при наличии помех. Показаны преимущества метода ЭО применительно к задаче синтеза итерационных многоканальных систем.

3.                  Рассмотрены выражения для ошибок и варианты структурной схемы неравноточной итерационной двухканальной (N=2) воспроизводящей системы с контролем выходной величины () по замкнутому циклу и при наличии помех ()() и ()=(), приведенных по входам соответственно первого и второго каналов управления.

Полученные результаты подтверждают принципиальную возможность эффективного решения проблемы повышения точности воспроизведения полезного сигнала при наличии аддитивных возмущений с помощью неравноточных итерационных многоканальных систем с эталонной настройкой каналов.

1.                  Клубникин П.Ф. Объединенные следящие системы с двумя приводами // Автоматика и телемеханика. – 1959.– Т. ХХ. – №2. – С.161 – 175.

2.                  Осмоловский П.Ф. Итерационные многоканальные системы автоматического управления. – М.: Сов. радио, 1969. – 256 c.

3.                  Следящие приводы. В 2-х кн. / Под ред. Б.К. Чемоданова. Кн. Первая. – М.: Энергия, 1976. – 480 c.

4.                  Никольский А.А. Точные двухканальные следящие электроприводы с пьезокомпенсаторами. – М.: Энергоатомиздат, 1988. – 160 с.

5.                  Худяев А.А. Алгоритм расчета дисперсий ошибок многоканальных итерационных систем методом рекуррентных уравнений // Автоматика. – 1986. – №6. – С. 43 – 52.

6.                  Осмоловский П.Ф., Худяев А.А. Влияние запаздывания входных координат на динамическую точность двухканальной итерационной измерительной системы // Автоматика. – 1990. – №2. – С. 35 – 42.

7.                  Худяев А.А., Московец В.И. Эффективность итерационных алгоритмов построения следящих систем с неидентичными входными координатами // Автоматизация технологических процессов и производств. – Харьков: ХАИ, 1988. – С. 130 – 143.

8.                  Никольский А.А. Новые высокоточные электроприводы с пьезокомпенсаторами для станков, механизмов и приборов // Электротехника. – 1993. – №1. – С. 27 – 31.

9.                  Многоканальные итерационные системы управления: Учебное пособие / Б.И. Кузнецов, А.А. Худяев, И.Н. Богаенко и др. – К.: НПК “КИА”, 1998. – 224 с.

1                    Худяев А.А., Гвоздева Е.В. Автоматизированное проектирование итерационных многоканальных систем с эталонной настройкой каналов // Вестник ХГПУ. Сборник научных трудов. Тематический выпуск 113. – Харьков: ХГПУ, 2000. – С. 49 – 56.

2                    Худяев А.А. Оптимальные структуры каналов управления и оценка точности в классе итерационных многоканальных воспроизводящих систем // Проблемы автоматизированного электропривода. Теория и практика: Вестник ХГПУ. Спец. выпуск. – Харьков: ХГПУ, 1998. – С. 52 – 54.

3                    Двухякорный линейный синхронный привод обрабатывающего центра / Б.И. Кузнецов, А.А. Худяев, И.М. Некрасов, В.И. Русаев // Электротехника. – 1993. – №4. – С. 11 – 18.

4                    Худяев А.А. Многоканальный прецизионный линейный электропривод для станков инструментального производства // Проблемы автоматизированного электропривода. Теория и практика: Вестник ХГПУ. Спец. выпуск. – Харьков: ХГПУ, 1998. – С. 279 – 280.