Автоматика.
    Автоматизация.
        Электротехнические
            комплексы и системы.

УДК 548.4:548.52.621.315.59

АНАЛИЗ ФЛУКТУАЦИЙ РАЗМЕРА РАСТУЩЕГО КРИСТАЛЛА (НА ПРИМЕРЕ ЛЕГИРОВАННЫХ МОНОКРИСТАЛЛОВ КРЕМНИЯ, ВЫТЯГИВАЕМЫХ ИЗ РАСПЛАВА ПО МЕТОДУ ЧОХРАЛЬСКОГО)

Краснов В.А., Прохорович А.В., Шутов С.В., Деменский А.Н.

Введение

Процессы непрерывной направленной кристаллизации различных материалов (металлов, полупроводников, монокристаллических диэлектриков и т.п.) широко используются в различных промышленных технологиях [1 – 3]. При этом условия последующих переделов заготовок таких материалов, или их применений, определяют требования к формообразованию (прутки, ленты, слитки, формы, близкой к цилиндрической,  проволоки и т.п.). Зачастую основным размером кристалла, который контролируется в процессе направленной кристаллизации, является диаметр или аналогичный ему параметр. Это связано с тем, что данный параметр, отражающий процессы радиального разрастания кристалла, в большей мере подвержен влиянию текущих  характеристик технологического процесса, чем параметры, которые определяют осевой рост, например, длина и характер осевого распределения примесей. Последние, в основном, задаются начальными условиями технологического процесса: массой исходной загрузки в тигель, заданным номинальным размером кристалла, коэффициентом распределения примеси и т.п.

Между тем, известно, что комплексные производственные потери от некачественного регулирования радиального размера кристаллизующейся заготовки, могут достигать 10 – 15% объема невозвратных потерь материала при серийном производстве [4]. Поэтому вопросам исследования влияния условий кристаллизации на процессы формообразования слитков (заготовок) материалов и процессам автоматического регулирования их основных параметров уделяется большое внимание [5, 6], а  сами эти проблемы достаточно актуальны в связи с постоянным развитием технологий новых материалов.

В данной работе на примере технологического процесса вытягивания из расплава слитков монокристаллического кремния проведен анализ флуктуаций диаметра слитков в процессе вытягивания, предложен феноменологический подход, который позволил установить на количественном уровне связь диаметра кристалла с основными технологическими параметрами процесса вытягивания и физико–химическими характеристиками материала.

Краткая полуэмпирическая теория

Схематический разрез теплового узла установки вытягивания монокристаллов кремния по методу Чохральского представлен на рис. 1.

Надо отметить, что в большинстве промышленных технологий вытягивания монокристаллов кремния из расплава по методу Чохральского инактивный флюс не используется, однако вытягивание данным методом из расплава соединений А³В⁵ и А²В⁶ стехиометрического состава, к примеру, без использования флюса  практически невозможно. Поэтому ради общности рассмотрения эта позиция приведена на рис. 1. Технологический аспект процессов вытягивания слитков монокремния из расплава по методу Чохральского подробно изложен, например, в монографии [7] и в данной работе затрагивается только в той мере, которая необходима для изложения и понимания основного материала статьи.

Предварительно сделаем следующие допущения:

1. Теплоотвод при вытягивании монокристалла осуществляется преимущественно через затравку (соответствующий контур обычно охлаждается водой) и через поверхность монокристалла за счет излучения тепла.

2. Температура  поверхности кристалл–расплав  приблизительно  одинакова,  из–за выделения скрытой теплоты кристаллизации, являющейся авторегулирующим фактором, т.е. градиенты температуры на поверхности раздела фаз жидкость – твердое не существенны.

3. Вращение кристалла или тигля [7, 8]  создает   температурное   поле с осевой симметрией (см. рис. 1), где Т_ор – изотерма в расплаве, вдали от фронта кристаллизации; Т_е – равновесная температура ликвидуса системы кремний – примесь; Т_к – температура на фронте кристаллизации.

4. Радиальный градиент температуры в расплаве не учитывается.

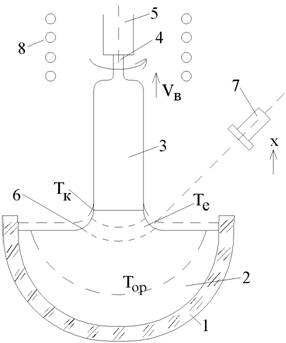
Рис. 1 Схема метода Чохральского:

1 – кварцевый тигель, 2 – расплав кремний - легирующая примесь, 3 – вытягиваемый монокристалл кремния, 4 – монокристаллическая затравка, 5 – затравкодержатель, 6 – слой инактивного флюса, 7 – оптическая головка с фотоэлектрическим датчиком, 8 – фоновый нагреватель

В таком случае условием предотвращения отрыва расплава (жидкости) от поверхности монокристалла является следующее [9]:

где       V_в –   скорость вытягивания слитка,

V –    скорость роста, которая равна  скорости  передвижения  теплового  потока через границу раздела жидкая – твердая фаза.

Далее учитываем составляющую V только в направлении оси роста, т. е. V = V_x.

Определим V_x, считая, что форма границы раздела фаз плоская, из уравнения температуропроводности Фика.  Дополнительно положим, что температура зависит только от координаты x и времени t, т.е. T = T (x, t)

             Раскрыв  частную производную в левой части выражения (2)  получим                                                                     

Заметим, что параметр V_x характеризует нелинейность функции T (x, t) и описывает, как будет показано ниже, составляющую скорости роста при условии плоского фронта кристаллизации.

В случае сферической границы раздела фаз можно показать [9], что радиальная составляющая скорости роста V_r связана с осевой V_x и радиусом сферы r следующим соотношением:

или        

            Из выражений (1) и (5) следует, что, если V_r = V_в, то

            Проанализируем формулу (6):

а) r  → ∞, случай плоской границы раздела (рис. 2а)

б) V_в > V_x, вогнутый в расплав фронт кристаллизации (рис. 2б),

в) V_в < V_x, выпуклый в расплав фронт кристаллизации (рис. 2в).

Из рис. 2 следует, что наличие сил поверхностного натяжения на границе кристалл–расплав приводит к образованию мениска. В общем случае вид фронта кристаллизации (плоский, вогнутый или выпуклый в расплав) не зависит от вида мениска. Однако колебания диаметра выращиваемого монокристалла,  которые определяются формой фронта кристаллизации, связаны с видом мениска (его образующей). Следовательно, процессы разрастания, уменьшения и поддержания постоянным диаметра слитка могут быть индицированы видом мениска. На этом принципе реализуют оптические системы контроля диаметра слитков кремния, других полупроводников и полупроводниковых соединений, вытягиваемых из расплава по методу Чохральского [6, 10]. При этом параметрами регулирования процесса являются скорость вытягивания и/или температура расплава.

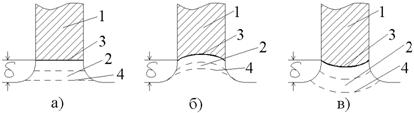
Рис. 2 Формы фронта кристаллизации (граница жидкость – твердое при

вытягивании монокристаллов методом Чохральского):

а) плоский, б) вогнутый и в) выпуклый в расплав фронт кристаллизации:

1 – монокристалл, 2 – расплав, 3 – граница раздела фаз жидкость – твердое (фронт кристаллизации), 4 – изотермы в расплаве, δ – высота мениска в области контакта кристалл–расплав.

Недостатками оптических систем являются сложность контроля оптическим методом формы мениска расплава, влияние окружающей среды (процессы испарения из расплава, наличие флюса, неоднородности мениска) на регистрируемый системой сигнал. Поэтому на практике часто переходят к массовому принципу контроля диаметра слитков [11], которому присущи известные недостатки механических систем регулирования и контроля.

В дальнейшем рассмотрении дополнительно предположим, что любые градиенты температур в расплаве пренебрежимо малы (рис. 1). Радиальные градиенты температуры на фронте кристаллизации отсутствуют. Это достигается вращением кристалла и/или тигля [7,12], а также вытягиванием растущего слитка в зону постоянной температуры, создаваемую фоновыми нагревателями  (рис. 1, поз. 8). Высота мениска δ (рис. 2)  мала (случай больших диаметров слитков), поэтому теплоотводом через область мениска можно пренебречь.

Тогда уравнение тепломассопереноса на границе раздела фаз, являющееся частным случаем так называемого уравнения Реньяна [13] (от уравнения Реньяна его отличает отсутствие слагаемого, связанного с градиентом температуры в расплаве), примет вид

где         L –         удельная теплота плавления кристалла,

dm/dt –    скорость   перехода   вещества   в  твердое  состояние (прирост массы кристалла в единицу времени),

kS –          коэффициент теплопроводности кристалла,

dT/dx –    осевой градиент температур в системе расплав-кристалл,

T –           текущее значение температуры в области раздела фаз жидкость – твердое,

S_K –          площадь  изотермической  поверхности  отвода  тепла от фронта кристаллизации, которая в первом приближение равна площади поперечного сечения кристалла. 

Выразим из уравнения (8) производную dx/dt, представляющую собой максимальную скорость вытягивания монокристалла из расплава V_max:

где       dm = ρ  dV,

            ρ –       плотность твердой фазы (кристалла),

dV –    элементарный объем кристаллизующейся фазы.

При   малых dx,  т.е.   dx → 0, можно   считать,   что dV = S_k · dx. Следовательно, dm = ρ · S_k · dx. Подставив последнее выражение в уравнение (9) получим.

где       dT/dx – осевой градиент температуры на фронте кристаллизации (8)*.

Отметим, что на практике значение V_max ~ на 30-50% меньше, чем определенное по формуле (10). Это связано, как с ростовыми и технологическими ограничениями, так и с вышеприведенными нашими предположениями.

Пользуясь выражением (10) и сделанным нами допущением 1 о том, что отвод тепла от слитка осуществляется преимущественно через боковую поверхность (для  слитков диаметром > 60 мм это экспериментально обосновано), найдем связь скорости роста (вытягивания) монокристалла при V_p → V_max с диаметром D растущего монокристалла. При этом считаем, что на участке слитка, где D = const, т.е. на участке автоматического поддержания диаметра, форма слитка цилиндрическая (так называемая цилиндрическая часть слитка)**.

В выражении (10) представим dx как dx = dV/S_K, тогда 

Поскольку, согласно предположению,  отвод тепла осуществляется преимущественно через боковую поверхность монокристалла, то из условия непрерывности теплового потока имеем

где       l' – высота цилиндрической части слитка от фронта кристаллизации до зоны постоянной температуры, т. е. до места расположения фонового нагревателя нагревателя в установке вытягивания слитков.

При этом элементарный объем dV равен

Подставив выражения (12) и (13) в формулу (11), получим

Согласно экспериментальным данным (см., например, [14]), распределение температуры вдоль оси слитка имеет экспоненциальный характер и может быть аппроксимировано следующей зависимостью:

где       To –         температура на фронте кристаллизации,

α –            коэффициент, характеризующий степень „затухания” температуры по оси слитка от To к Tф – температуре фонового нагревателя (рис. 1, поз. 8).

На основе известного свойства экспоненциальный функции можно принять

где          l' – расстояние „затухания” температуры по оси слитка (12).

Заметим, также, что величина α равна V_x, или V (см. формулы (1,3), т.е. равняется скорости перемещения теплового потока через границу раздела фаз. Величину α, а, следовательно, и l', можно для заданного материала  определить достаточно точно заранее.

Подставив l',  определенное  из выражения  (16), в формулу (14), получим:

С учетом сделанных предположений распределение температуры в системе жидкость-твердое (расплав–кристалл) будет следующим (рис. 3).

Считаем, что в расплаве на расстоянии от фронта кристаллизации, примерно равным высоте полумениска расплава δ/2, распределение температуры T(x) экспоненциальное, соответствующее выражению (15). Тогда для определения градиента температуры на фронте кристаллизации dT/dx продифференцируем выражение (15):

Знак „минус” в формуле 18 свидетельствует о том, что с увеличением расстояния x от фронта кристаллизации температура уменьшается, и, следовательно, градиент температуры отрицателен.

Подставив выражение dT/dx из (18) в формулу (17) с учетом знака,  получим

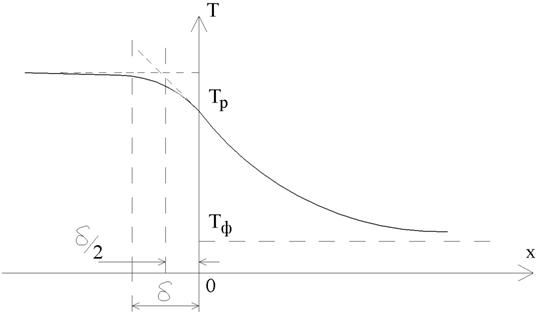
Рис. 3 График осевого распределения температуры в ростовой системе:

δ – высота мениска расплава (см. рис. 2), T_o – температура расплава

При x = 0 (точки на фронте кристаллизации, рис. 3)

или, перейдя к зависимости диаметра D от переменных процесса кристаллизации, имеем

В случае выращивания легированных монокристаллов кремния значение T_о = T_л, где T_л – равновесная температура ликвидуса бинарной системы кремний-примесь, которая практически всегда меньше температуры плавления кремния. Величина A = k_S / (ρ · L) – константа, так как значения k_S и ρ слабо зависят от температуры.

Из формулы (21) следует, что диаметр монокристалла, вытягиваемого из расплава, зависит от отношения T_о / V_р. При этом скорость вытягивания V_в = V_p является „чисто внешней”, т.е. задаваемой системой выращивания характеристикой. Поэтому флуктуации диаметра D растущего кристалла определяются, в основном, флуктуациями температуры T_о = T_л на и вблизи фронта кристаллизации (по крайней мере, на расстоянии полумениска расплава). Флуктуации T_о зависят от конвективных потоков тепла в ростовой камере установки Чохральского, инерционности систем поддержания теплового режима, „уносом” тепла путем испарения атомарно-молекулярных пучков вещества из расплава, в том числе и легко испаряющихся примесей, передачей тепла излучением и другими причинами.

Считая, что флуктуации диаметра монокристалла ∆D малы по сравнению с величиной самого диаметра D, найдем зависимость ∆D, представляющую собой текущее значение отклонения диаметра в процессе роста от номинального значения D_о, от флуктуаций температуры на фронте кристаллизации.

Продифференцируем выражение (21) по температуре при V_р = const . С учетом знака производной dD/dT имеем dD/dT = –A/V_р. Или, переходя к конечным разностням флуктуаций диаметра ∆D и температуры ∆T, получим ∆D/∆T = –A/V_р, откуда

где       ∆D = D' – D_о, ∆T = T' – T_о,

D', D_о –    текущее   значение  диаметра  монокристалла  и  его  номинальное  значение, соответственно,

T', T_о –     текущее значение температуры на фронте кристаллизации и равновесное значение температуры, определяемое кривой ликвидуса кремний– примесь, соответственно.

Из формулы (22) имеем

Проведем анализ формулы (23).

При T_о > T', ∆D = D' – D_о > 0, т.е. реализуется режим так называемого „намерзания” кристаллизующегося вещества (кремния)  на фронте кристаллизации слитка.

При T_о < T', ∆D = D' – D_о < 0 – режим „подплавления” области, прилегающей к фронту кристаллизации монокристалла.

Следовательно, в соответствии с формулами (21) – (23), АСУТП вытягивания слитков кремния, содержащая подсистему контроля и регулирования диаметра монокристалла в процессе вытягивания, должна при флуктуациях ∆T варьировать T_р (рис. 3) путем регулирования температуры нагревателя расплава и/или скорости V_в. В этом случае измеряемой величиной, является T_о (T_л системы кремний-примесь).

Количественные оценки флуктуаций диаметра монокристалла

Используя полученные соотношения, оценим величины минимальных нерегулируемых флуктуаций диаметра ∆D при вытягивании из расплава слитков монокристаллов кремния различных диапазонов номиналов диаметра.

а. 60 ≤ D ≤ 100 мм.

В этом диапазоне диаметров так называемая крейсерская скорость вытягивания слитков V_в = V_р составляет V_р = 0.2 – 0.3 см/мин. Примем значения флуктуаций температуры ∆T ≤ 2.0 °С, т.е. равными пределу разрешения  средств контроля температуры, например, термопар или высокоточных пирометров при температурах выше 1200 °С. Значение удельной теплоты плавления L для кремния ~ 264 кал/г, плотность кремния ρ = 2.33 г/см³,  коэффициент теплопроводности k_S = 0.05 кал/(с · см · °С). В этом случае определенное  по формуле (22)  значение ∆D ≤ ±0.5мм.

b. 100 ≤ D ≤ 150 мм.

При V_р = 0.1 – 0.2 см/мин и характерных значениях остальных параметров, таких же, как в п. а, величина ∆D составляет ∆D ≤ ±1.0 мм.

c. D > 150 мм.

V_р = 0.05 см/мин, ∆D ≤ ±2.0 мм.

Полученные значения ∆D являются одними из основных исходных параметров при разработке систем автоматического регулирования диаметра монокристаллов кремния, вытягиваемых из расплава по методу Чохральского, поскольку задают характеристики точности поддержания диаметра монокристалла.

Обсуждение полученных результатов

Одной из важных тенденций современной технологии монокристаллов кремния является переход к большим, более 150 мм, диаметрам монокристаллов. Это связано, прежде всего, с ростом потребления монокремния в наземной солнечной энергетике [14]. В промышленности для широкомасштабного получения такого кремния используют технологии, основанные на методе Чохральского [15,16]. Как правило, соответствующее ростовое оборудование оснащено системами автоматического поддержания диаметра монокристалла в процессе вытягивания. Проведенный анализ свидетельствует об увеличении нерегулируемых флуктуаций диаметра монокристалла при переходе к выращиванию  слитков с диаметром более 150 мм. Данная тенденция особенно характерна для процессов роста по методу Чохральского сильнолегированных монокристаллов. В этом случае повышение уровня  ∆D за счет роста величины ∆T (см. формулу (23) и вышеприведенный ее анализ) связано дополнительно с локальными процессами концентрационного переохлаждения расплава кремний–примесь при вытягивании слитка кремния [17]. Последнее обстоятельство также необходимо учитывать при разработке системы автоматического регулирования диаметра ростовых установок, работающих по методу Чохральского. Особенно, в  части, связанной с регулированием скорости вытягивания и требованиями повышения быстродействия в реальном масштабе времени системы измерения и обработки данных о температурах  расплава и мениска.

Выводы

Выполнен краткий анализ процессов тепломассопереноса при непрерывной направленной кристаллизации слитков монокремния из расплава методом Чохральского. Полученные соотношения (10), (17), (21)–(23) устанавливают связь диаметра монокристалла со скоростью вытягивания слитка, температурой или градиентом температур на фронте кристаллизации (температурой мениска расплава кремний–примесь), теплофизическими и физико–химическими характеристиками кремния. Показано, что выражения (22) и (23) позволяют оценить уровень нерегулируемых (минимальных) флуктуаций диаметра монокристалла в процессе вытягивания слитка из расплава. Сделаны оценки уровня этих флуктуаций при выращивании монокристаллов кремния промышленных диаметров. Установлена динамика размера флуктуаций диаметра при переходе к росту легированных и сильнолегированных монокристаллов кремния больших (более 150 мм) диаметров, а также отмечено ее влияние на построение и реализацию систем автоматического регулирования диаметра монокристалла в установках, работающих по методу Чохральского.

Несмотря на узкоспециальный характер выполненных исследований, на примере анализа роста легированных монокристаллов кремния,  вытягиваемых из расплава по методу Чохральского, предложенный подход, на наш взгляд,  обладает достаточной общностью и может быть применен к широкому набору процессов непрерывной направленной кристаллизации моно– и поликристаллических материалов и их различных заготовок, изготавливаемых в условиях контролируемого формообразования.

ЛИТЕРАТУРА

1.                   Целиков А. И. Новые   процессы и агрегаты в металлургии и технологии металлов. Вестник АН СССР, 1975. – № 6. – С. 3 – 20.

2.                  Багдасаров Х.С. Высокотемпературная кристаллизация из расплава. – М.: Физматлит, 2004. – 173 с.

3.                  Мильвидский М., Освенский В. Фундаментальные проблемы российской металлургии на пороге XXI века. Монография в 4–х томах. – М.: Рос. акад. естеств. наук, 1998. – т. 4, 147 с.

4.                  Нашельский А. Я. Производство полупроводниковых материалов. – М.: Металлургия, 1982. – 312 с.

5.                  Шашков Ю. М.   Выращивание     монокристаллов    методом   вытягивания. – М.: Металлургия, 1982. – 203 с.

6.                  Лейбович В. С., Сухарев В. А., Шушков В. М., Федоров В. А.     Автоматическое управление процессом роста монокристаллов. – Приборы и системы управления. – 1975. – № 5. – С. 7 – 9.

7.                  Технология полупроводникового кремния / Фалькевич Э. С., Пульнер Э. О., Червоный И. Ф. и др. – М.: Металлургия, 1992. – 408 с.

8.                  Liepold M. H., O’Donnell T. P., Hagan M. A. Materials of construction for silicon crystal growth. - J. Cryct. Growth. – 1980. – 40. – P. 366–378.

9.                  Салли И. В., Фалькевич Э. С. Управление формой роста кристаллов. – К.: Научная мысль, 1989. – 160 с.

10.              Михляев С. В. Системы технического зрения для контроля геометрии выращиваемого кристалла. – Тр. Оптич.общ.им. Д. С. Рождественского: материалы VIII Межд.конф. “Прикл. оптика – 2008”, т. 1, СПб: ООО “ЦТТ”, 2008. – С. 62 – 66.

11.              Bardsley W., Hurle D.T.J, Joyce G. C. The weighing method of automatic Chochralski Crystal Growth. 1 Basic theory. – J. Cryst. Growth. – 1977. – № 40. – P. 13–20.

12.              Нашельский А. Я.    Технология    спецматериалов   электронной техники. – М.: Металлургия, 1993. – 352 с.

13.              Реньян В. Р. Технология полупроводникового кремния / В. Р. Реньян ; пер. с англ. под ред. Ю. М. Шашкова. – М.: Металлургия, 1969. – 335 с.

14.              Наумов А. В.   Производство         фотоэлектрических      преобразователей       и рынок кремниевого сырья в 2006-2010г.г. – “Изв. вузов. Материалы электронной техники”. – 2006. – № 2. – C. 29 – 35.

15.              Мильвидский М. Г. Полупроводниковый кремний на пороге XXI века. – “Изв. вузов. Материалы электронной техники”. – 2000. –  № 1. –  C. 14 – 18.

16.              Silicon wafers for photovoltaics. Technical information. Bayer solar GmbH.

17.              Kim K. M. Interface morphological instability in Chochralski silicon crystal growth from  heavity Sb – doped melt. – J. Electrochem. Soc., 126, 875 (1979).