УДК 531.7
ЕНЕРГЕТИЧНИЙ ПІДХІД ДО АНАЛІЗУ СТІЙКОСТІ РУХУ ВИМІРЮВАЛЬНОЇ ГОЛОВКИ КООРДИНАТНО-ВИМІРЮВАЛЬНОЇ МАШИНИ
Іволгіна Т.О.
Вступ
Застосування прямого методу Ляпунова для аналізу стійкості руху динамічних систем дозволяє значно розширити область застосування аналітичних методів дослідження. Задача ускладнюється відсутністю загального способу побудови функції Ляпунова.
Сам А. М. Ляпунов і багато його послідовників для вирішення окремих задач в якості функції Ляпунова часто застосовували математичне вираження повної і кінетичної енергії динамічної системи [2 - 4].
При матрично-векторному трактуванні диференціальних рівнянь узагальнених сил [5-7] методи аналізу процесу перетворення енергії не потрапили до поля зору дослідників. Застосування математичного вираження приросту повної енергії при відхиленні руху динамічної системи від незбуреного до цього часу не розглядалося. Вираз для оцінки повної енергії динамічної системи задовольняє вимогам, що пред'являються до функції Ляпунова, в тому випадку, коли в якості незбуреного руху прийнято стан спокою в початку координат, відносно яких описується рух динамічної системи.
В якості початкових даних в теорії стійкості руху використовуються рівняння збуреного руху, які є математичною моделлю досліджуваної динамічної системи на збуреннях, тобто відхиленнях узагальнених координат від їх значень при незбуреному русі.
Постановка задачі
Побудуємо функцію Ляпунова на основі системи звичайних диференціальних рівнянь з дійсними коефіцієнтами шляхом проведення певної послідовності перетворень.
При складанні диференціальних рівнянь за аргументи виберемо параметри, які однозначно визначають стан системи. За аналогією з теоретичною механікою при аналізі руху, описуваного диференціальними рівняннями, можуть бути використані поняття узагальнених координат і узагальнених сил. Тоді доданки рівнянь сприйматимуться як математичні вирази узагальнених сил, тобто як величини, рівні коефіцієнтам при приростах узагальнених координат у виразах повної елементарної роботи діючих на систему сил [1].
Розв'язання задачі
Для динамічної системи, що має ![]() ступенів свободи, система рівнянь збуреного руху має наступний вигляд:
ступенів свободи, система рівнянь збуреного руху має наступний вигляд:
![]() ;
; ![]()
![]() (1)
(1)
де ![]() - дійсні коефіцієнти пропорційності між значенням узагальненої сили та
- дійсні коефіцієнти пропорційності між значенням узагальненої сили та ![]() -ї похідної відхилення, що є функціями часу та відхилення;
-ї похідної відхилення, що є функціями часу та відхилення; ![]() -
- ![]() -та похідна відхилення по
-та похідна відхилення по ![]() -й узагальненій координаті.
-й узагальненій координаті.
Рівняння (1) є однорідними, так як ними описується вільний рух системи із збуреного стану, що визначається початковими відхиленнями від незбуреного ![]() .
.
Кількість енергії, що затрачується динамічною системою при переході з незбуреного стану у збурений, може бути визначена почленним інтегруванням рівняння (1) в межах від ![]() до
до ![]() , якщо в праву частину рівняння підставити значення збурюючої
, якщо в праву частину рівняння підставити значення збурюючої ![]() . Інтегрування доцільно виконувати по часу, замінивши
. Інтегрування доцільно виконувати по часу, замінивши ![]() на
на ![]() та межі інтегрування: нижню – на
та межі інтегрування: нижню – на ![]() , коли система знаходиться у незбуреному стані
, коли система знаходиться у незбуреному стані ![]() , верхню – на
, верхню – на ![]() , коли система знаходиться в початкових умовах та збурююча дія припинилась (
, коли система знаходиться в початкових умовах та збурююча дія припинилась (![]() =0). Тоді рівняння роботи узагальнених сил прийме вигляд
=0). Тоді рівняння роботи узагальнених сил прийме вигляд
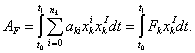 (2)
(2)
Кількість енергії, перетвореної в процесі цього руху, рівна роботі внутрішніх сил динамічної системи.
Структуру енергетичних потоків і узагальнених сил, що беруть участь в їх утворенні, можна простежити на прикладі диференціального рівняння ![]() -го порядку, опустивши індекс
-го порядку, опустивши індекс ![]() , що відповідає номеру ступеня вільності.
, що відповідає номеру ступеня вільності.
Робота, виконувана потенціальними силами динамічної системи,
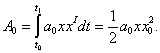 (3)
(3)
Енергія, перетворена в результаті роботи потенціальних сил, затрачена на зміну потенціальної енергії динамічної системи. Приріст енергії залежить лише від значення відхилення і не залежить від тривалості інтервалу інтегрування.
Кількість енергії, перетвореної силою, яка пропорційна першій похідній відхилення,
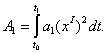 (4)
(4)
Напрям потоку енергії, перетворюваної за рахунок роботи цієї сили, залежить від знаку коефіцієнта ![]() , тобто від властивостей динамічної системи і тривалості інтервалу інтегрування, але не залежить від напряму швидкості. Енергія або розсіюється диссипативними силами, або вводиться в сферу перетворення силами прискорюючими, а потім акумулюється у вигляді приросту повної енергії.
, тобто від властивостей динамічної системи і тривалості інтервалу інтегрування, але не залежить від напряму швидкості. Енергія або розсіюється диссипативними силами, або вводиться в сферу перетворення силами прискорюючими, а потім акумулюється у вигляді приросту повної енергії.
Кількість енергії, перетвореної кінетичною силою, пропорційною другій похідній відхилення за часом, визначається рівнянням
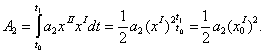 (5)
(5)
Ця енергія затрачується на зміну кінетичної складової повної енергії динамічної системи.
Кількість енергії, перетвореної силою, пропорційною третій похідній відхилення,
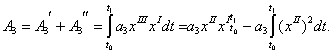 (6)
(6)
Енергія, перетворена за рахунок роботи цієї сили, частково затрачується на утворення приросту повної енергії (![]() ) динамічної системи і частково (
) динамічної системи і частково (![]() ) розсіюється або вводиться в сферу перетворення в залежності від знаку коефіцієнта
) розсіюється або вводиться в сферу перетворення в залежності від знаку коефіцієнта ![]() .
.
Інтегруючи рівняння (2), що містить похідні відхилення більш високого порядку, одержимо вирази, що ілюструють роль цих узагальнених сил в процесі перетворення енергії:
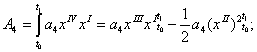 (7)
(7)
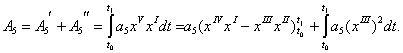 (8)
(8)
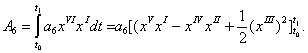 (9)
(9)
Доданки рівняння роботи внутрішніх сил динамічної системи можуть бути розділені – за роллю в процесі перетворення енергії – на дві групи: 1) доданки, абсолютна величина яких не залежить від тривалості інтервалу інтегрування, що визначають приріст повної енергії динамічної системи; 2) доданки, абсолютна величина яких залежить від тривалості інтервалу інтегрування, що визначають разом з роботою збурюючи дій, енергетичний зв’язок системи з оточуючою середою.
Підставимо вирази (3) – (9) в рівняння (2), розмістивши в лівій частині доданки першої групи, а в правій – другої:
![]()
![]()
де ![]() - приріст повної енергії динамічної системи, одержаний при початкових умовах збуреної дії.
- приріст повної енергії динамічної системи, одержаний при початкових умовах збуреної дії.
Аналогічно можна розглянути процес перетворення енергії в ході збуреної дії. Взявши за основу рівняння (1), одержимо
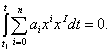
Інтегрування здійснюється у межах від моменту ![]() , коли відхилення досягнуло заданого значення
, коли відхилення досягнуло заданого значення ![]() та зовнішня дія припинилась (
та зовнішня дія припинилась (![]() ), до довільного моменту
), до довільного моменту ![]()
У відповідності до означення стійкості за Ляпуновим тривалість збуреної дії не обмежена, тому верхня межа змінна. Змінивши відповідно межі інтегрування, скористаємося виразами (3) – (9) та одержимо рівняння роботи
![]()
![]() (10)
(10)
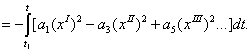
Рівнянням (10) визначається різниця значень приросту повної енергії динамічної системи. Значення ![]() рівне кількості енергії, що віддається оточуючому середовищу або вводиться в сферу перетворення з середи в процесі збуреної дії за інтервал часу
рівне кількості енергії, що віддається оточуючому середовищу або вводиться в сферу перетворення з середи в процесі збуреної дії за інтервал часу ![]() .
.
Взявши похідну по часу від обох частин рівняння (10), одержимо вираз
![]()
що визначає потужність розсіювання енергії або виведення її в сферу перетворення в процесі збуреної дії.
Висновки
1. Математичний вираз приросту ![]() повної енергії динамічної системи є неперервною дійсною функцією, що відповідає вимогам, які пред'являються до функції Ляпунова.
повної енергії динамічної системи є неперервною дійсною функцією, що відповідає вимогам, які пред'являються до функції Ляпунова.
2. Похідна за часом приросту повної енергії визначає потужність сил взаємодії динамічної системи з навколишнім середовищем при збуреному русі.
3. Приріст повної енергії є скалярною величиною, що дозволяє одержати сумарний приріст повної енергії для багатовимірної динамічної системи простим сумуванням окремих приростів по кожній узагальненій координаті (ступені вільності динамічної системи).
4. Оскільки при побудові функцій здійснюється інтегрування і диференціювання за часом, запропонований спосіб може використовуватися для аналізу рухів, описуваних рівнянням як з постійними коефіцієнтами, так і з коефіцієнтами, залежними від часу.
Для побудови функції Ляпунова і її похідної за часом, взятої в силу рівняння збуреного руху, необхідно виконати наступні операції:
- встановити параметри незбуреного руху та скласти систему рівнянь збуреного руху; скласти рівняння роботи узагальнених сил та виконати інтегрування доданків рівнянь в межах ![]() і
і ![]()
- виділити доданки, що визначають роботу, яка затрачується на приріст повної енергії ![]() і роботу сил взаємодії системи з середовищем, та взяти похідну
і роботу сил взаємодії системи з середовищем, та взяти похідну ![]() .
.
Розглянутий спосіб використаний з позитивним результатом при розв’язанні прикладів, що містяться в роботі [2].
On an example of a disturbed motion equations with fixed factors the structure of the generalized forces on their ratio to the process of energy transformation is considered and the way of the Lyapunov’s function construction is offered
1. Тарг С.М. Краткий курс теоретической механики. М.: Наука, 1967.
2. Меркин Д.Р. Введение в теорию устойчивости движения. М.: Наука, 1971.
3. Анопольский Л.Ю., Иргетов В.Д., Матросов В.М. Способы построения функции Ляпунова // Итоги науки и техники. Сер. Общая механика. М.: Винити, 1975. Т.2, С.53-87.
4. Развитие и применение метода функций Ляпунова // Сб. науч. тр. Новосибирск: Наука, 1992.
5. Зубов В.И. Аналитическое построение функции Ляпунова // Докл. РАН. 1994. Т.335, №6. С.888-893.
6. Аминов А.Б., Сиразетдинов Т.К. Функции Ляпунова для исследования устойчивости в целом нелинейных систем // Прикладная математика и механика. 1985. Т.49, вып.5.
7. Малкин И.Г. Теория устойчивости движения. М.: Наука, 1966.
Ответы на вопросы [_Задать вопроос_]
Читайте также
Современные технические средства, комплексы и системы
Краснов В.А., Прохорович А.В., Шутов С.В., Деменский А.Н. Анализ флуктуаций размера растущего кристалла (на примере легированных монокристаллов кремния, вытягиваемых из расплава по методу Чохральского)Завальнюк И.П. Управление высокопроизводительной экструзией неоднородных материалов
Долина В.Г., Писаренко А.В. Синтез складної багатовимірної системи управління випарною станцією на основі рефрактометричних вимірювань
Стопакевич А.А., Тодорцев Ю.К. Анализ современного состояния систем управления брагоректификационными установками спиртового производства
Поливода В.В. Современные компьютерные технологии в АСУ на хлебоприёмном предприятии
Ладанюк А.П., Українець А.І., Кишенько В.Д. Управління автоматизованими технологічними комплексами харчових виробництв на основі сценарного підходу
Ковриго Ю.М., Фоменко Б.В. Врахування обмежень для підвищення якості функціонування систем регулювання енергоблоків ТЕС і АЕС
Евдокимов А.В., Китаев А.В., Агбомассу В.Л. Исследование причин, определяющих вращение рамки с током в магнитном поле после воздействия на нее внешнего импульса
Аппазов Э.С. Применение твердых растворов InGaN в фотовольтаике
Кузнєцов Ю.М., Дмитрієв Д.О. Програмно математичний апарат керування виконавчим органом багатокоординатних верстатів нових компоновок
Черевко О.И., Ефремов Ю.И., Одарченко А.М., Одарченко Д.М, Агафонова Ю.Ю. Теоретическое обоснование перспективного биконического резонатора для СВЧ-устройств при переработке растительного сырья
Хобин В.А. Бабиков А.Ю. Системы экстремального управления молотковыми дробилками с функцией гарантированного соблюдения тепловых режимов их электродвигателей.
Стадниченко В.Н. Исследование влияния изменения эксплуатационных нагрузок на свойства металлокерамических слоёв полученных с использованием трибовосстанавливающих составов
Ісаєв Е.А., Наговський Д.А., Чернецька І.Е. До вибору факторів, що характеризують окомкування тонкоподрібнених залізорудних матеріалів
Федоровский К.Ю., Лунев А.А. Теплоотдача погружного пластинчатого теплообменника системы охлаждения энергоустановок морских технических средств
Федоровский К.Ю., Владецкий Д.О. Интенсификация теплоотвода замкнутых систем охлаждения энергоустановок морских технических средств.
Пономарьов Я.Ю., Ладанюк А.П., Іващук В.В. Досвід використання нечітких регуляторів в системі атоматизації випарної установки.
Левченко А.А., Кравчук О.И. Эквивалентный макромодуль процесса технического обслуживания радиотехнических средств.
Ладанюк А.П., Кишенько В.Д., Ладанюк О.А. Системна задача управління біотехнологічними процесами.
Тернова Т.І. Алгоритм оцінювання деформацій рапорту періодичних об'єктів
Рожков С.А., Федотова О.Н. Алгоритм обучения системы распознавания автоматической системы разбраковки тканей
Пупена О.М, Ельперін І.В, Ладанюк А.П. Особливості проектування комп’ютерно-інтегрованих систем управління
Квасніков В.П., Кочеткова О.В. Проектування координатно–вимірювальної машини на нейронних мережах
Водічев В.А., Мухаммед М.А. Дослідження системи стабілізації потужності різання металообробного верстата з фази-регулятором
Шутов С.В., Аппазов Э.С., Марончук А.И., Самойлов Н.А. Методика испытания термофотовольтаических преобразователей
Хобин В.А. Повышение качества формирования смесей средствами интеллектуализации алгоритмов управления порционным дозированием
Терновая Т.И. Автоматическая система разбраковки тканей с печатным рисунком методом компенсации информационных потоков
Рожков С.А., Бражник Д.А. Использование нейросетевых структур для построения систем распознавания образов
Місюра М.Д., Кишенько В.Д. Математичні моделі технологічних процесів пивоварного виробництва як об’єктів автоматизації
Ладанюк А.П., Власенко Л.О. Автоматизоване управління бізнес-процесами в комп’ютерно-інтегрованих структурах підприємства
Жукова Н.В., Литвинов В.І. Вирішення проблеми погодженого руху валків з неоднаковими катаючими діаметрами профілезгинальних станів
Денисова А.Е., Тодорцев Ю.К., Максименко И.Н. К вопросу об автоматизации интегрированной установки теплоснабжения с возобновляемыми источниками энергии
Бессараб В.И. Компьютеризированная система управления водоотливным хозяйством угольных шахт по критерию минимума энергозатрат
Хобин В.А. Регулятор переменной структуры для объектов технологического типа
Тонконогий В.М. Трехконтурная АСУ нанесением ионно-плазменного покрытия на режущий инструмент.
Колесникова Е.В., Кострова Г.В. Формирование базы данных АСУТП дуговой сталеплавильной печи.
Водічев В.А. Автоматизована система керування швидкостями робочих рухів то-карного верстата для підвищення ефективності обробки торцевих поверхонь.
Бергер Е.Г., Дмитрієв Д.О., Бергер Є.Е., Діневич Г.Ю. Синтез строфоїдографів за методом параметричних сімей.
Бабак В.П., В.Н. Стадніченко, О.Г. Приймаков Прогнозування надійності, дов-говічності та витривалості авіаційних матеріалів
Бабак В.П., Стадниченко В.Н., Приймаков О.Г., Токарчук В.В. Прогнозування витривалості авіаційних матеріалів .
Куцак Р.С. Використання методу координатного еталону в задачах автоматизації контролю якості тканини.
Попруга А.Г. Усовершенствование электрических нагревателей по критерию экономии энергии.
Пашковский А.А., Далечин А.Ю. Система регистрации спектров фотолюминес-ценции
Никольский В.В., Цюпко Ю.М. Применение пьезоэлектрических датчиков в сис-теме кондиционирования воздуха судовых систем микроклимата.
Крапивко Г.И., Хлопёнова И.А. Повышение коэффициента полезного действия кремниевых фотоэлектронных преобразователей методом лазерной гравировки.
Кихтенко Д.А. Управление шаговыми двигателями в микрошаговом режиме, оп-тимизация управления.
Горохов В.А. Автоматизированная транспортно-складская система в текстильной и легкой промышленности.
Водічев В.А. Система стабілізації потужності різання фрезерного верстата з взаємозв'язаним керуванням швидкостями робочих рухів.
Шутов С.В., Аппазов Э.С., Марончук А.И. Испытание фотоэлектрических преобразователей в условиях экстремальных температурных колебаний.
Худяев А.А. К проблеме повышения точности воспроизведенияв классе многоканальных воспроизводящих систем с эталонной настройкой каналов.
Тверезовський В.С., Бараненко Р.В. Принцип побудови елементів вимірювальних систем, представлених цифровими програмно керованими давачами.
Никольский В.В., Сандлер А.К. Моделирование процессов в вискозиметре с пьезоэлектрическим приводом.
Марончук И.Е., Андронова Е.В., Баганов Е.А., Курак В.В. Использование метода импульсного охлаждения насыщенного раствора-расплава для формирования наноразмерных структур InSb в матрице GaSb.
Водічев В.А. Аналого-цифровий регулятор режиму металообробки для верстатів з числовим програмним керуванням.
Блинов Э.И., Кравцов В.И., Кравцов А.В., Недбайло А.Н. Управление гибкими протяженными объектами направленными силовыми воздействиями.