УДК 662.753.22+665.733.3

Вступ

Однією з найбільш актуальних проблем нафтопродуктозабезпечення є втрати нафтопродуктів, значною частиною яких є втрати від випаровування при проведенні різних технологічних операцій, зокрема, зберігання, транспортування та розподілу. Сьогодні 40% нафти виливається у море під час аварій танкерів, 27% – при перекачці по нафтопродуктопроводам, 16% складають втрати при зберіганні та біля 0,5% надходить до води під час буріння [1].

Світові статистичні дані вказують на те, що загальні втрати нафти та нафтопродуктів від випаровування коливаються у межах 0,5–1,7% від загального об’єму переробленої сировини, в Україні 3–7% [2-27]. Якщо у середньому прийняти величину втрат на рівні 5%, то при переробці 19,4 млн. т нафти на рік (дані 2002 р.) збиток складе 970 тис. т. Таким чином, у процесах зберігання, транспортування та розподілу втрачається ¼ частина видобутої власної нафти.

Проблемі запобігання втратам нафти та продуктів її переробки від випаровування завжди приділялася велика увага вчених і практиків. Проте проблема втрат існує дотепер і вимагає невідкладного вирішення. У глобальному масштабі втрати нафтопродуктів – проблема енергетичної та екологічної безпеки.

Постановка завдання

Аналіз літературних джерел дозволяє зробити висновок про те, що використання понтонів, плаваючих криш, систем уловлювання легких фракцій та інших заходів не дозволяє успішно вирішувати проблему втрат легких фракцій, а запобігає втрати тільки незначної частини вуглеводнів. Відомі технічні розробки, як правило, орієнтовані на величезні капіталовкладення або, у кращому випадку, мають локальний характер.

Тому було поставлене завдання розробити технологічну систему рекуперації пари моторних палив, в основі якої лежить технічна простота і висока ефективність на підставі використання сорбційних процесів.

Вирішенння задачі

Теоретичною базою для створення технологічної системи запобігання втратам від випаровування стала сучасна теорія випаровування вуглеводневих рідин, розроблена Л.С.Лейбензоном, О.С.Колєсніковим М.І.Білоконем, М.М.Константиновим, В.І.Черникіним, І.П.Бударовим, О.С. Ірисовим, Г.Ф. Большаковим, О.О. Гурєєвим, Ф.Ф. Абузовою та їх послідовниками [2,6-14] і теорія сорбції газів і пари, описана Брунауером [28], К.М.Ніколаєвським [29], О.М.Серпіоновою [30], Д.В.Сивухіним [31], М.В.Кельцевим [32], І.Є.Неймарком [33], М.М.Дубініним [34], Ю.Г.Фроловим [35].

Сучасні уявлення про випаровування рідин ґрунтуються на теорії подібності до процесів теплообміну, поглибленому розумінні молекулярного і конвективного перенесення тепла і речовини – розвитком гідродинамічної теорії теплообміну, а також теорій примежового шару та будови рідини.

Виходячи з того, що сучасні уявлення про випаровування вуглеводневих рідин ґрунтуються на теорії подібності до процесів теплооміну, нами в основу вибору методу внаслідок багатогранності та складності явищ розроблювальної технологічної системи покладено поєднання феноменологічного (експериментально-аналітичного) та теоретичного (структурного) методів, яке передбачає складання детального математичного опису елементарних процесів, що входять до складного через застосування експериментально-аналітичних залежностей.

При проведенні даного моделювання дотримувалися основні вимоги та умови для побудови моделей [36,37]. Як відомо, основною умовою моделювання є подібність об’єкта та його моделі; чітке апріорне уявлення сутності фізико-хімічних процесів, що протікають в об’єкті; ізоморфізм цих процесів; уміння математично описувати ці процеси та використовувати методи моделювання.

Таким чином, завданням моделювання є комплексний опис процесів, що відбуваються при великих і малих “диханнях” резервуарної ємкості, таких як випаровування, масообмін, сорбція, десорбція, конденсація.

Розглянемо процес випаровування вуглеводневої рідини у гіпотетичній замкнутій резервуарній ємкості, що обладнана сорбційним модулем у складі технологічної системи рекуперації пари палива. У результаті випаровування вуглеводневого палива в резервуарі об’ємом Vр, в якому знаходиться вуглеводнева рідина, створюється насичена пароповітряна суміш (ППС). При підвищенні температури Т і, відповідно, збільшенні тиску газу р, клапан “тиск” “дихального” клапана спрацьовує (мале “дихання”) і потік газу із швидкістю w проходить через прошарок сорбенту товщиною (висотою) H. При цьому частина молекул вуглеводневої пари адсорбується прошарком сорбенту. Після вирівнювання тиску клапан закривається і прошарок сорбенту прогрівається до температури Тн. При цьому відбувається процес десорбції вуглеводнів, які потім потрапляють до модуля конденсації з температурою Тк, де конденсуються й стікають у резервуар. Період циклу tc адсорбції (десорбції) складає 90–120 хв. Після N циклів у сорбенті накопичуються не десорбовані вуглеводні масою Δm, тобто має місце гістерезис.

Над поверхнею рідини одночасно відбуваються процеси випаровування, дифузії, конвекції та конденсації пари. Швидкість пересування повітря у результаті конвективних токів може бути прийнятою 0,05–0,10 м/с.

Для розрахунку процесів рекуперації надзвичайно важливо визначити кількість летючої речовини при будь-якій технологічній операції. А.В.Ликовим [38] було виведено формулу для визначення кількості рідини, що випарувалась

,

де А – коефіцієнт, що залежить від коефіцієнта Рейнольдса (при Re = 200–20000 А = 0,5Re0,58, а при Re = 20000–200000 А = 0,85Re0,76); М – молярна маса рідини, що випаровується; D – коефіцієнт дифузії пари рідини, що випаровується; R – газова стала пари рідини, що випаровується; Т – абсолютна температура, яка дорівнює середньому арифметичному значенню від температури поверхні рідини та температури повітря;

Fвип – поверхня випаровування; t – тривалість випаровування;  – тиск насиченої пари рідини при температурі рідини t; – тиск насиченої пари рідини у повітрі; l – довжина шляху потоку повітря над поверхнею випаровування.

Набір даних за наведеною формулою для розрахунку кількості речовини, що випарувалася, демонструє існування труднощів для проведення таких розрахунків.

Тому для подальшого проведення моделювання скористаємось такими міркуваннями. Припустимо, що тиск у газовому просторі (ГП) резервуара дорівнює барометричному тиску, температура – температурі навколишнього середовища, концентрація пари однакова по об’єму ГП, а ППС підкоряється рівнянню стану газів і закону Дальтона. Таким чином, маса пари палива mп.п. буде розраховуватись за формулою

m_п.п. = Z V_р r_п.п. С_s = Z V_р r_п.п. ,

де Z – коефіцієнт заповнення резервуара; Vр – об’єм резервуара, м3; rп.п. – густина пари палива, кг/м3;  – тиск насиченої пари палива; Рб – барометричний тиск, кПа.

Враховуючи те, що молекула пари має кінетичну енергію вищу від кінетичної енергії молекули рідини, концентрацію молекул над рідиною можна визначити за формулою Больцмана [39]. Після деяких перетворень формула для визначення густини насиченої пари палива у ГП резервуара буде мати такий вигляд

,

де – густина рідини; Мп – молярна маса вуглеводневої пари; L – теплота випаровування (Lвип = 8,75 × Tкип + 4,571 × Tкип × lg Tкип; Tкип = (tп.к. + 4 tп.к. + tк.к.) / 6); R – універсальна газова cтала.

Адсорбція пари вуглеводневої рідини прошарком сорбенту

Швидкість адсорбції, або кількість адсорбованої з потоку рідини за одиницю часу одиницею об’єму шару зернистого поглинача, визначається, зазвичай, за рівнянням кінетики сорбції

,

де a – кількість адсорбованої речовини на одиницю довжини сорбенту за період t; b – кінетичний коефіцієнт, який показує кількість речовини (у кг), що передається з потоку пароповітряної суміші 1 м3 сорбенту за 1 с при різниці концентрації речовини у парогазовому потоці c та концентрацією пари у, яка знаходиться у стані рівноваги з поглиненою речовиною (1 кг/м3), 1/с .

 Застосовуючи теорію подібності, можна стверджувати, що рівняння кінетики сорбції є рівнянням масопередачі, а кінетичний коефіцієнт – коефіцієнтом масопередачі.

У загальному випадку процес адсорбції складається з таких етапів:

1) дифузія молекул речовини, що сорбується, із потоку пароповітряної суміші до зовнішньої поверхні частин сорбенту (зовнішній масообмін);

2) дифузія молекул речовини, що сорбується, по порам сорбенту (внутрішня дифузія);

3) власне сорбція внутрішньою сорбційною поверхнею поглинача.

Кількість речовини, що внаслідок молекулярної дифузії через ламінарний примежовий шар підводиться з потоку до поверхні поглинача, визначається, виходячи із закону Фіка [2]. Ця кількість речовини повинна бути рівною кількості поглиненої речовини, яка визначається за рівнянням кінетики сорбції. Тому

,

де Fпог – поверхня поглинання в одиниці об’єму шару поглинача, м2/м3;  – градієнт концентрації (зміна концентрації на одиницю довжини шляху речовини, що дифундує).

 Наведене рівняння є математичною аргументацією умов переходу речовини на межі поділу твердої та газоподібної фаз.

За допомогою теорії подібності можна, не інтегруючи диференційні рівняння, отримати з них методом подібного перетворення критерії подібності, а потім замінити ці диференційні рівняння залежністю між критеріями подібності (критеріальним рівнянням). Але вид такої залежності знаходять через експеримент. Існуючі приклади критеріальних рівнянь детально розглянуто у праці [30], тому скористаємось іншим підходом та виведемо рівняння для маси вуглеводневої пари, що накопичені у циліндричному прошарку сорбенту.

Ізотерму сорбції , щo є характеристикою сорбенту, опишемо ізотермою Ленгмюра (ізотерма І типу):

 ,                                                     (1)

де g – коефіцієнт Генрі; a = сonst (характеризує лінійне розширення).

При малих концентраціях пари, вважаючи, що a = 0, з (1) можна отримати ізотерму сорбції Генрі. З (1) знаходимо вираз для y:

                                                                                                            (2)

Сорбент, що знаходиться у конструкції технологічної системи (сорбційному модулі), являє собою кульки діаметром 3–5 мм [40]. Кульки розміщені у циліндрі з боковими стінками висотою Н і діаметром d. Через торці циліндра із швидкістю w прокачується ППС. Швидкість прокачування ППС через сорбент визначається різницею тисків у середині р_р та зовні резервуара р_б . За законом Бернуллі

швидкість прокачування пароповітряної суміші буде складати:

,

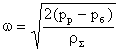де – густина ППС; m_пов – маса повітря у резервуарі.

Після низки математичних перетворень на базі системи нелінійних диференційних рівнянь [39] (у часткових похідних), що описують процес адсорбції вуглеводневої пари прошарком сорбенту (граничні й початкові умови ; ;  відповідають відсутності адсорбованої пари у порах сорбенту у початковий момент часу t = 0 (0 £ а £ Н) і наявності концентрації пари с_o на вхідному торці циліндру із сорбентом z у довільний момент часу t > 0 (a = H; ; с = с_o = const; температура газу та адсорбенту – сталі величини)

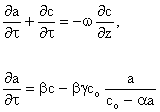
отримано рівняння, що описує масу вуглеводневої пари m_п.п^а, накопичену у циліндричному прошарку сорбенту діаметром d_вн і довжиною Н за одиницю часу t:

 ^.

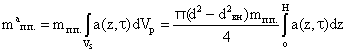Одна з основних стадій будь-якого адсорбційного процесу – десорбція поглинутої пари – може здійснюватися різними методами: через підвищення температури прошарку адсорбенту; вакуумуванням системи; продувкою газом-носієм і т.п. [29,30,32,34]. Але у всіх випадках необхідною умовою результативного здійснення десорбційної стадії є наявність мінімального температурного рівня, який забезпечував би швидке видалення адсорбата.

Десорбція вуглеводневої пари, що поглинулась прошарком сорбенту

З аналізу літературних джерел випливає, що теоретичні основи стадії десорбції розроблені значно слабше, аніж теорія статики, кінетики та навіть динаміки адсорбції. Зважаючи на факт труднощів математичного опису десорбційних процесів більшість дослідників пропонують вирішення проблеми для окремих випадків із рядом припущень, а у деяких випадках – обмежитись емпіричними вирішеннями для окремих систем.

На відміну від прямого процесу (адсорбції), в якому визначальним фактором є дифузійні процеси, при оберненому процесі (десорбція) вирішального значення набуває швидкість “відривання” молекул від поверхні адсорбенту.

На сьогодні прийнято десорбційні процеси описувати за допомогою так званого “відносного методу розрахунку кінетики десорбції”, який оснований на припущенні того, що після видалення адсорбата з об’єму адсорбційних порожнин молекули, що залишились, утворюють мономолекулярний шар у відсутності взаємодії між адсорбованими молекулами, тобто за теорією Ленгмюра, швидкість десорбції визначається за рівнянням:

,

де q – ступінь заповнення поверхні; k₁, k₂ – константи швидкості прямого та оберненого процесів; р – тиск у системі.

Крім того, існує метод відносного розрахунку десорбційних кривих нормальних вуглеводнів парафінового ряду за сіткою десорбційних кривих стандартної речовини (наприклад, н-пентану) [32].

Кінетику десорбції описує рівняння

 ,

де q_р – ступінь заповнення поверхні при досягненні рівноваги; е = 2,7183; b – коефіцієнт, пропорційний фактору Больцмана (n_о exp (– E_дес / RT ); n_о – кількість центрів адсорбції на одиниці поверхні; E_дес – енергія активації десорбції).

Виходячи з вищевказаного, приходимо до того, що для опису десорбційних процесів у розроблювальній технологічній системі, найбільш правильним буде застосування емпіричного підходу через побудову кривої десорбції. А за отриманим рівнянням, що описує кінетику десорбції, можна оцінити кількість десорбованої речовини m_д.

Конденсація вуглеводневої пари

Для створення умов, необхідних для конденсації вуглеводнів, нами обґрунтовано можливість застосування термоелектричних холодильників через використання термоелектричних батарей [39-42]. Десорбована вуглеводнева пара захоплюється конвективними потоками і проходить через ребра термоелектричного модуля (ТЕМ), де підтримується відповідна температура (наприклад, мінус 10 – мінус 40^оС). При цьому, у результаті теплообміну пара охолоджується та конденсується на поверхні ребер (гетерогенна конденсація). Згідно рівняння капілярної конденсації Кельвіна ln (p_к/p_р) = ± 2sV_м/(RTr) конденсація відбувається на поверхні ядер конденсації (зародків) дуже малих розмірів. Внаслідок цього реакційна здатність сконденсованої речовини більше ніж макрофази. Для того щоб сконденсована речовина не поверталась у попередню фазу й конденсація продовжувалась, необхідне пересичення у даній системі. У загальному випадку швидкість конденсації визначається двома стадіями: утворенням ядер (зародків) конденсації й ростом зародків [35].

Масу конденсату наближено можна описати таким рівнянням

Dm_к = V_конд Dr ,

де V_конд – об’єм камери, де відбувається конденсація пари; Dr – зміна густини насиченої пари при зміні температури.

Як відомо, густина насиченої пари пов'язана з температурою. Базуючись на цих міркуваннях, приходимо до наступного опису маси конденсату

 ,

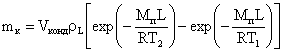де Т₂ – температура пари на вихідному торці циліндра із сорбентом; Т₁ – температура холодних радіаторів термоелектричного модуля.

Теплоту, що необхідно витратити для конденсації пари палива можна описати таким рівнянням:

Q_к= c_р ^п.п. m_п.п. (T₂ – T₁) ,

де c_р ^п.п. – теплоємність пари палива (середня величина теплоємності пари палива складає 1,6 кДж/(кг ^oК) при 0^оС); T₁ – температура десорбції; T₂ – температура конденсації.

Сумарна теплота, що необхідна для нагрівання сорбенту та забезпечення процесів десорбції й конденсації, описується формулою:

,

де Dt – тривалість роботи термоелектричного модуля.

Для визначення кількості батарей обов’язково необхідно враховувати основне правило роботи ТЕМ: для поглинання енергії (1 частина холоду) необхідно витратити 3 частини тепла (виділення енергії). Тому опис теплової потужності батареї оцінюється як три частини холодильної потужності Q_max:

.

Базуючись на приведених міркуваннях, можна знайти кількість батарей W для формування ТЕМ

.

Прогнозування та оцінку ефективності розроблювальної технологічної системи нами запропоновано здійснювати за показником ефективності рекуперації пари Е_р.п.

.

Висновок

Описані дослідження дозволяють удосконалити математичну модель технологічної системи рекуперації моторних палив, що створює необхідне теоретичне підґрунтя для прогнозування експлуатаційних параметрів цієї системи, підбору термоелектричних батарей та розрахунку ефективності запобігання втратам від випаровування при використанні такої системи на будь-якому підприємстві нафтопродуктозабезпечення.

Для реалізації моделі можна використовувати будь-яке програмне середовище. Отриманий програмний продукт буде корисним для використання і систематизації експериментальних даних.

1.                  Фащук Д.Я. Трагедии на “Божьей дороге” // Химия и жизнь. – 2003. – № 3. – С. 22–27.

2.                  Бойченко С.В. Раціональне використання вуглеводневих палив: Монографія. – К.: НАУ, 2001. – 216 с.

3.                  Чичкин А.А. Звено технического прогресса // Газовая промышленность. – 1991. – № 1. – С. 2–4.

4.                  Шидловський А.К., Ковалко М.П., Вишневський І.М. Паливно-енергетичний комплекс України на порозі третього тисячоліття. – К.: Укр. енциклопедичні знання, 2001. – 400 с.

5.                  Шпак П.Ф. Раціональне використання власних ресурсів нафти й газу – головний фактор розвитку нафтогазового комплексу України // Нефть и газ. – 2000. – № 8. – С. 86–90.

6.                  Константинов Н.Н. Борьба с потерями от испарения нефти и нефтепродуктов. – М.: Гостоптехиздат, 1961. – 260 с.

7.                  Бударов В.П. Потери от испарения моторних топлив при хранении. – М.: РИО ВНИИСТ Главгаза СССР, 1961. – 139 с.

8.                  Хизгилов И.Х. Сохранение качества нефтепродуктов при их транспорте и хранении. – М.: Недра, 1965. – 192 с.

9.                  Аренбристер В.В. Технико-экономический анализ потерь нефти и нефтепродуктов. – М.: Химия, 1975. – 160 с.

10.              Серегин Е.П. Экономия горючего. – М.: Воениздат, 1980. – 144 с.

11.              Абузова Ф.Ф. Борьба с потерями нефти и нефтепродуктов при их транспортировке и хранении. – М.: Недра, 1981. – 260 с.

12.              Гуреев А.А., Камфер Г.М. Испаряемость топлив для поршневых двигателей. – М.: Химия, 1982. – 264 с.

13.              Яковлев В.С. Хранение нефтепродуктов. Проблема защиты окружающей среды. – М.: Химия, 1987. – 150 с.

14.              Зеркалов Д.В. Экономия нефтепродуктов: Справочное пособие. – М.: Недра, 1990. – 191 с.

15.              Prater N.H. How to calculate vapor losses // Petroleum Journal. – 1955. – V. 9. – № 4. – P. 31–34.

16.              Hoge T. Hydrocarbon vapor recovery eased // Oil and Gas Journal. – 1974. – № 24. – P. 146–150.

17.              Regulation of Fuels and Fuel Additives: volatility Regulations for Gasoline and Alcohol Blends Sold in Calendar Years 1992 and Beyond. Final Rule // Federal Register (Environmental Protection Agency). – 1990. – Vol. 55. – № 112. – P. 40–80.

18.              Comments of the American Petroleum Institute Concerning EPA’s August 19. 1987 Proposed Regulation of Fuels and Fuel Additives and Regulation of Refuelling Emissions // Docket Nos. (API). – 1988. – A-85–21. February 11.

19.              Умергалин Т.Г., Хафизов А.Р., Мухамедзянов А.Х., Абызгильдин Ю.М. Технология улавливания низкокипящих бензиновых фракций из резервуаров // Нефтяное хозяйство. – 1989. – № 10. – С. 6–9.

20.              Быков В.А. Как снизить потери нефтяных углеводородов // Нефтяное хозяйство. – 1990. – № 2. – С. 9–10.

21.              Маликов Б.А., Михальков П.В. Пути сокращения потерь углеводородов // Нефтяное хозяйство. – 1990. – № 5. – С. 6–8.

22.              Тронов В.П., Сахатбутдинов Р.З., Закиев Ф.А., Рахимов И.В., Ибрагимов И.В. Эксплуатация систем улавливания паров нефти на промыслах // Нефтяное хозяйство. – 1996. – № 12. – С. 50–52.

23.              Хамидуллин Ф.Ф., Шайхутдинов М.Я., Гибадуллин А.А., Закиев Ф.А., Кавеев Х.З., Ибрагимов Н.М. Технологические потери углеводородов на объектах ОАО “Татнефть” и пути их сокращения // Нефтяное хозяйство. – 1998. – № 12. – С. 25–56.

24.              Тронов В.П., Сахатбутдинов Р.З., Фаттаров Р.Б., Закиев Ф.А., Ибрагимов И.В. Совершенствование технологий утилизации углеводородов на нефтяных промыслах // Нефтяное хозяйство. – 1998. – № 1. – С. 57–59.

25.              Хамидуллин Ф.Ф., Шайхутдинов М.Я., Гибадуллин А.А. Эффективность применения современных систем улавливания легких фракций нефти // Нефтяное хозяйство. – 1999. – № 6. – С. 52–53.

26.              Шпак О.Г. Нафта і нафтопродукти. – К.: Ясон-К, 2000. – 370 с.

27.              Кириллов Н.Г. Системы бездренажного хранения сжиженного природного газа // Химическое и нефтегазовое машиностроение. – 2003. – № 3. – С. 11–13.

28.              Брунауер С. Адсорбция газов и паров. Т. 1. – М.: Издательство иностранной литературы, 1948. – 781 с.

29.               Николаевский К.М. Проектирование рекуперации летучих растворителей с адсорберами периодического действия. – М.: Оборонгиз, 1961. – 238 с.

30.              Серпионова Е.Н. Промышленная адсорбция газов и паров. – М.: ВШ, 1969. – 419 с.

31.              Сивухин Д.В. Термодинамика и молекулярная физика. – М.: Наука, 1975. – 552 с.

32.              Кельцев Н.В. Основы адсорбционной техники. – М.: Химия, 1976. – 512 с.

33.              Неймарк И.Е. Адсорбенты и катализаторы. – К.: Наукова думка, 1978. – 147 с.

34.              Дубинин М.М. Исследование адсорбционных процессов и адсорбентов. – Ташкент: ФАН, 1979. – 324 с.

35.              Фролов Ю.Г. Курс коллоидной химии (Поверхностные явления и дисперсные системы): Учебник для вузов. – М.: Химия, 1982. – 400 с.

36.               Веников В.А., Веников Г.В. Теория подобия и моделирования. – М.: Высш. шк., 1984. – 439 с.

37.              Струтиський В.Б. Математичне моделювання процесів та систем механіки. – Житомир: ЖіТі, 2001. – 612 с.

38.              Лыков А.В. Тепломассообмен: Справочник. – М.: Энергия, 1978. – 479 с.

39.              Бойченко О.В., Аксьонов О.Ф., Бойченко С.В., Дзедолік І.В. Разработка математической модели системы предотвращения потерь углеводородов от испарения в составе “дыхательного” клапана резервуарной емкости // Збірник наукових праць інституту проблем моделювання в енергетиці НАН України. – 2002. – Вип. 14. – С. 145–155.

40.              Бойченко С.В., Бойченко О.В., Швець О.В., Ільїн В.Г. Дослідження кінетики адсорбції парів різних видів нафтового палива // Нафтова і газова промисловість. – 2001. – № 3. – C. 61–64.

41.              Бойченко О.В., Аксьонов О.Ф., Бойченко С.В. Обґрунтування можливості застосування сорбентів і термоелектричних охолоджуючих пристроїв для запобігання природних втрат нафтових палив // Вісник НАУ. – 2001. – № 2. – С. 136–143.

42.              Іванов С.В., Бойченко С.В. Теплова модель процесу конденсації пари палива // Доповіді НАН України. – 2002. – № 5. – С.117–120.