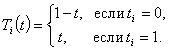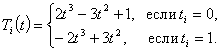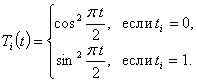УДК 519.6
МЕТОД БАРИЦЕНТРИЧЕСКОГО УСРЕДНЕНИЯ ГРАНИЧНЫХ ПОТЕНЦИАЛОВ ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ
Хомченко А.Н., Литвиненко Е.И.
Введение
Большинство современных вычислительных методов в теории потенциала ориентировано на ЭВМ. Наибольшее распространение получили методы конечных разностей (МКР), конечных элементов (МКЭ), граничных элементов (МГЭ), контрольных объемов (МКО), Монте-Карло и другие. Для практической реализации этих методов, как правило, требуются значительные объемы машинной памяти и времени вычислений. В качестве альтернативы выступает простой, надежный и алгоритмичный метод барицентрического усреднения, обеспечивающий вполне приемлемую точность вычислений.
Анализ предшествующих публикаций
Идея использовать барицентрические координаты симплекса (треугольника, тетраэдра) в быстрых алгоритмах метода Монте-Карло возникла в конце 80-х годов прошлого века [1,2] и была реализована под названием – способ вращения симплекса (СВС). Важным шагом в развитии и усовершенствовании метода было установление глубоких связей между барицентрическим усреднением и дискретными аналогами интегрального критерия Привалова гармоничности функций [3]. Позже стало понятно, что идеи барицентрического усреднения полезны не только в задачах эллиптического типа [4]. Вся история развития геометрии, механики, вычислительной математики свидетельствует о том, что барицентрическое усреднение (впрочем, как и любое другое) – надежный рецепт усовершенствования математической модели. Конкретные примеры описаны в [5-11].
Цель работы – показать три альтернативных варианта барицентрического усреднения электростатического потенциала от системы точечных зарядов, расположенных в вершинах куба.
Основная часть
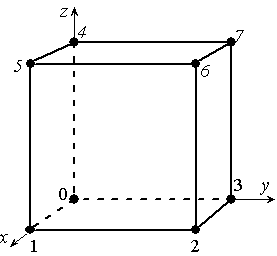
Пусть в вершинах куба (![]() ,
,![]() ,
,![]() ) значения потенциального поля известны. Требуется найти потенциальное поле внутри куба (рис. 1).
) значения потенциального поля известны. Требуется найти потенциальное поле внутри куба (рис. 1).
|
|
|
|
Рис. 1 Элемент в форме куба с узлами в вершинах |
|
В этой задаче нетрудно усмотреть аналогию с классическим результатом А.Мёбиуса, который в 1827 г. нашел ответ на вопрос о том, какие массы следует поместить в вершинах заданного треугольника, чтобы данная точка была центром тяжести (барицентром) этих масс. Для решения такой задачи Мёбиус ввел специальные координаты (барицентрические), которые привели к созданию барицентрического исчисления. В отличие от классической задачи Мёбиуса (на симплексе) обобщенная задача на мультиплексе (рис. 1) решается неоднозначно. Здесь вступают “в спор” (Е.С.Вентцель), по крайней мере, три подходящих модели потенциального поля. В эту группу можно включить и четвертую модель, реализующую случайные блуждания по узлам пространственной ортогональной решетки (статистическая модель).
Потенциал внутри области выражается через граничные потенциалы путем взвешенного усреднения
|
|
(1) |
где ![]() - известные значения потенциала в вершинах куба
- известные значения потенциала в вершинах куба ![]() . Функции
. Функции ![]() имеют типичные свойства базиса: каждая из них в “своем” узле
имеют типичные свойства базиса: каждая из них в “своем” узле ![]() равна единице, в остальных узлах обращается в нуль. Кроме того,
равна единице, в остальных узлах обращается в нуль. Кроме того,
|
|
(2) |
Лучше использовать функции, монотонные внутри куба. Задача сводится к поиску функций ![]() , обладающих указанными свойствами.
, обладающих указанными свойствами.
Функцию ![]() удобно представить в виде произведения трех функций, каждая из которых зависит от одного аргумента
удобно представить в виде произведения трех функций, каждая из которых зависит от одного аргумента ![]() ,
, ![]() или
или ![]() . Заметим, что координаты вершин куба состоят только из
. Заметим, что координаты вершин куба состоят только из ![]() и
и ![]() . Это позволяет в каждом координатном направлении
. Это позволяет в каждом координатном направлении ![]() ограничиться лишь двумя функциями
ограничиться лишь двумя функциями ![]() и
и ![]() .
.
В зависимости от выбранного базиса можно предложить три варианта барицентрического усреднения граничных потенциалов.
I вариант. Трилинейный базис.
В этом случае каждая функция базиса равна произведению функций вида:
|
|
Например, ![]() . Аналогично определяются остальные семь функций.
. Аналогично определяются остальные семь функций.
II вариант. Трикубический базис.
Этот базис конструируется из многочленов Кунса. При этом
|
|
Например, ![]() .
.
III вариант. Тригонометрический базис.
В этом случае
|
|
Например, ![]() .
.
Заметим, что второй и третий базисы обеспечивают дополнительную гладкость поля ![]() на границе куба, хотя в данной задаче, как и в задаче Мёбиуса, необходимости в этом нет.
на границе куба, хотя в данной задаче, как и в задаче Мёбиуса, необходимости в этом нет.
Расчеты показывают, что в данной области существует 19 особых точек, в которых все три базиса дают совпадающие результаты. Особые точки: центр куба, центры граней, центры ребер. Наличие этих точек стабилизирует поле потенциала так, что максимальная погрешность по сравнению с апостериорной монте-карловской оценкой не превышает 3,5%.
Следует отметить, что трилинейный базис состоит из гармонических функций как в дифференциальном смысле (по Лапласу), так и в интегральном смысле (по Привалову). Второй и третий базисы удовлетворяют интегральному критерию гармоничности. При подстановке этих функций в уравнение Лапласа образуются невязки, каждая из которых равна нулю в среднем по области. При этом суммарная невязка от всех восьми функций обращается в нуль.
Выводы
Предложенные в работе базисы пригодны для практической реализации в методе барицентрического усреднения (МБУ). Этот метод существенно уменьшает объем необходимой памяти ЭВМ и резко сокращает время вычислений по сравнению с классическим методом Монте-Карло и методом конечных разностей.
ЛИТЕРАТУРА:
1. Хомченко А.Н.Способ вращения симплекс-элемента в строительной механике /А.Н. Хомченко, Л.И. Камаева //Респ. конф. “Совершенствование методов расчета и проектирования совр. видов строит. конструкций”: Тез. докл. – Ровно, 1988. – С. 154 – 155.
2. Хомченко А.Н. Прискорений алгоритм методу Монте-Карло розв’язання задачі Діріхлє для рівняння Лапласа /А.Н. Хомченко //Вісник Київського держ. ун-ту ім. Т. Шевченка: Серія фіз.-мат. науки. – К.: КДУ, 1994. – С. 221 – 223.
3. Хомченко А.Н. Інтеграл Пуассона та ймовірнісні підходи до усереднення граничних потенціалів /А.Н. Хомченко //Інтегральні перетворення та їх застосування до крайових задач. Зб. наук. пр. – К.: І-т математики НАНУ, 1996. – Вип. 10. – С. 232 -234.
4. Зуб П.М. Компьютерная реализация методов барицентрического усреднения для задач эллиптического типа /П.М. Зуб, И.А. Лурье, А.Н. Хомченко // Вестник Херс.гос.техн.ун-та. − Вып. 1 (14). ― Херсон: ХГТУ, 2002. ― С. 46-49.
5. Хомченко А.Н. Модели взвешенного усреднения и кубатурные формулы /А.Н. Хомченко, О.В. Цыбуленко // Геом. та комп'ютерне моделювання. Зб. наук. пр. ― Харків: ХДУХТ, 2002. ― Вип. 2. ― С. 19-24.
6. Хомченко А.Н. О барицентрическом аспекте в математическом моделировании /А.Н. Хомченко, П.М. Зуб //Матем. модели в образовании, науке и промышленности. Сб. науч. тр. − С.- Петербург: МАН ВШ, 2003. − С. 85-91.
7. Хомченко А.Н. Барицентрические оценки электростатического поля в круге /А.Н.Хомченко, О.В. Цыбуленко, М.В. Дембровская //Автоматика. Автоматизация. Электрические комплексы и системы. − №1 (11). – Херсон: ХГТУ, 2003. ― С. 35-40.
8. Хомченко А.Н. Две модели усреднения граничных потенциалов на адаптируемом шаблоне /А.Н. Хомченко, Н.В. Валько, М.Т. Наджафов //Геом. та комп’ютерне моделювання. − Харків: ХДУХТ, 2004.− Вип. 8. − С.26-30.
9. Валько Н.В. Дискретні моделі зваженого усереднення граничних потенціалів /Н.В.Валько, О.І. Литвиненко, А.Н. Хомченко // Вісник Харк. націон. ун-ту. −№661. ― Харків: ХНУ, 2005. ― С. 52-60.
10. Хомченко А.Н. Об усреднении в математическом моделировании /А.Н. Хомченко, В.В. Крючковский // Вестник Херс. национ. техн. ун-ту.− Вып. 22. ― Херсон: ХНТУ, 2005. ― С. 340-343.
11. Хомченко А.Н. Модели барицентрического усреднения и одношаговые схемы случайных блужданий /А.Н. Хомченко, В.В. Крючковский //Матем. модели в образовании, науке и промышленности. Сб. науч. тр. − С.- Петербург: МАН ВШ, 2005. − С. 112-115.
Ответы на вопросы [_Задать вопроос_]
Читайте также
Моделирование объектов и систем управления
Соколов А.Е., Махова Е.О. Моделирование процесса принятия педагогического решения при компьютеризированном обученииСлавко О.Г. Порівняльний аналіз керування регулятором на основі локальної моделі керованого процесу та П-регулятором
Войтенко В.В., Дикусар Е.В, Ситников В.С. Определение частоты среза устройства сглаживания данных на основе метода скользящего среднего
Передерій В.І. Алгоритм визначення та оцінки характеристик ефективності комп’ютерних систем на початковій стадії проектування в умовах невизначенності
Ляшенко С.А, Ляшенко А.С. Оценка модели псевдолинейной регрессии
Ладієва Л.Р. Математична модель процесу газової мембранної дистиляції
Носов П.С., Косенко Ю.І. Нечіткі моделі і методи ідентифікації та прогнозу стану інформаційної моделі студента
Китаев А.В., Глухова В.И. Анализ работы синхронного двигателя с неявнополюсным ротором по данным каталога
Дорошкевич В.К., Пироженко А.В., Хитько А.В., Хорольский П.Г. К определению требований к системам увода космических объектов
Голінко І.М., Ковриго Ю.М., Кубрак А.І. Настройка системи керування за імпульсною характеристикою об’єкта
Яшина К.В., Садовой А.В. Комплексная математическая модель тепловых процессов, происходящих в дуговых электросталеплавильных печах
Шейник С.П., Рудакова А.В. Использование функций принадлежности для моделирования параметров распределенных объектов
Селяков Е. Б. Моделирование требований к техническим системам методами математической логики
Тодорцев Ю.К., Ларіонова О.С., Бундюк А.М. Математична модель контура теплопостачання когенераційної енергетичної установки
Кириллов О.Л. , Якимчук Г.С. Моделирование процесса управления системой перегрузки углеводородных жидких топлив
Шеховцов А.Н., Козел В.Н. Построение математической модели формирования распределенных систем
Китаев А.В., Глухова В.И. Анализ поведения генератора постоянного тока по данным каталога
Хомченко А.Н., Козуб Н.О. Задачі наближення функцій: від лагранжевих до серендипових поліномів
Хобин В.А., Титлова О.А. Определение температуры парожидкостной смеси в дефлегматоре АДХМ по результатам измерений температуры его поверхности
Григорова Т.М., Усов А.В. Вероятностно-статистическое моделирование маршрутизированных пассажиропотоков в крупных городах
Горач О.О., Тернова Т.І. Моделювання технологічного процесу одержання трести при використані штучного зволоження з урахуванням складу мікрофлори
Дубік Р.М., Ладієва Л.Р. Математична модель розділення неоднорідних рідких систем
Казак В.М, Лейва Каналес Родриго, Яковицкая Е.Ю. Моделирование динамики полета магистрального самолета на исследовательском стенде
Завальнюк И.П. Исследование процесса торможения автомобиля как критического режима динамической системы
Дмитриев С.А., Попов А.В. Построение портрета неисправностей проточной части газотурбинного двигателя на примере АИ-25
Русанов С.А., Луняка К.В., Клюєв О.І., Глухов Г.М. Математичне моделювання робочого процесу в апаратах з віброкиплячим шаром та розробка систем автоматизованого моделювання гідродинаміки віброкиплячих шарів
Боярчук В.П., Сыс В.Б. Экспериментальные исследования влияния технологии шлихтования на изменение жесткости текстильных нитей
Селін Ю.М. Використовування контекстних марківських моделей для аналізу дії промислових вибухів на будівельні конструкції
Рудакова А.В. Проблемы интеграции сложных систем
Передерій В.І., Касап А.М. Математична модель та алгоритм автоматизації розрахунку параметрів комп’ютеризованих систем працюючих у реальному часі
Передерий В.И., Еременко А.П. Математические модели и алгоритмы принятия релевантных решений пользователями автоматизированных систем с учетом личностных и внешних факторов на базе генетических алгоритмов
Михайловская Т.В., Михалев А.И., Гуда А.И. Исследование правил клеточных автоматов для моделирования процессов затвердевания квазиравновесных бинарных сплавов
Хомченко А.Н., Колесникова Н.В. Явление «сверхсходимости» в задаче Прандтля для уравнения Пуассона
Китаев А.В., Глухова В.И. Анализ работы трансформатора по данным каталога
Квасницкий В.В., Ермолаев Г.В., Матвиенко М. В., Бугаенко Б.В., Квасницкий В.Ф. Оценка применимости метода компьютерного моделирования к исследованию напряженно-деформиррованного состояния цилиндрических узлов
Китаев А.И., Глухова В.И. Анализ работы асинхронного двигателя по данным каталога
Шелестов А.Ю Имитационная модель взаимодействия GRID-узлов с очередью доступа к общей памяти
Chizhenkova R.A. Mathematical Aspects of Bibliometrical Analysis of Neurophysiological Investigations of Action of Non-ionized Radiation (Medline-Internet)
Хомченко А.Н., Козуб Н.А. Геометрическое моделирование дискретных элементов с криволинейными границами
Славич В.П. Модель автоматизованої системи управління потоками транспортних засобів
Маркута О.В., Мысак В.Ф. Программная реализация и исследование особенностей метода группового учета аргументов
Степанкова Г.А., Баклан І.В. Побудова гібридних моделей на основі прихованих марківських моделей та нейронних мереж
Бакшанська Т.Д., Рижиков Ю.Г., Тодорцев Ю.К. Математична модель процесу горіння природного газу з рециркуляцією продуктів згорання для цілей управління
Хомченко А.Н. Новые решения обобщенной задачи Бюффона
Передерий В.И., Еременко А.П. Математические модели и алгоритмы определения релевантности принимаемых решений с учетом психофункциональных характеристик пользователей при управлении автоматизированными динамическими системами
Ложечников В.Ф., Михайленко В.С., Максименко И.Н. Аналитическая много режимная математическая модель динамики газовоздушного тракта барабанного котла средней мощности
Ковриго Ю.М., Фоменко Б.В., Полищук И.А. Математическое моделирование систем автоматического регулирования с учетом ограничений на управление в пакете Matlab
Исаев Е.А., Наговский Д.А. Математическое описание влияния кривизны контактирующих тел на угол смачивания жидкости в межчастичном пространстве
Бідюк П.І., Литвиненко В.І., Кроптя А.В. Аналіз ефективності функціонування мережі Байєса
Тищенко И.А., Лубяный В.З. Математическое моделирование вокодера для определения оптимальной формы импульса сигнала возбуждения.
Николаенко Ю.И., Моисеенко С.В. Моделирование гармонического полиномиального базиса гексагона.
Козуб Н.А., Манойленко Е.С., Хомченко А.Н. Температурный тест для модифицированных базисов бикубической интерполяции.
Клименко А.К. Об упрощенном численном конструировании обратной модели динамического объекта.
Китаев А.В., Сушич Е.Ф. Расчет погрешностей измерительных трансформаторов.
Передерій В.І.,Касап А.М. Математична модель та алгоритм автоматизації розрахунку параметрів комп’ютеризованих систем працюючих у реальному часі
Шпильовий Л.В. Математична модель та алгоритм екстремального управління процесом осадження дисперсної фази суспензії.
Тулученко Г.Я. Інформаційний модуль експрес-пошуку точок еквівалентності процесу нейтралізації.
Тернова Т.І. Урахування морфогенетичного рівняння в математичній моделі тканини.
Попруга А.Г. Теоретические и экспериментальные исследования электрических нагревателей по критерию экономии энергии.
Китаев А.В., Сушич Е.Ф. Приложение положений теории дросселя и трансформатора к расчету и анализу электромагнитом переменного тока.