УДК 519.7
математична модель
контура теплопостачання когенераційної
енергетичної установки
Тодорцев Ю.К., Ларіонова О.С., Бундюк А.М.
У цей час в Україні простежується тенденція будівництва комбінованих джерел електро- і теплопостачання, установлюваних як в існуючих опалювальних котельнях, так і в знову споруджуваних. Це обумовлено світовою паливно-енергетичною кризою, наслідком якої є постійний ріст цін на енергоресурси.
Крім того, комунальна теплоенергетика України перебуває в критичному стані [4]. З метою підвищення ефективності функціонування комунальної теплоенергетики прийнято кілька державних програм [5]. Ефективне використання когенераційних установок на підприємствах комунальної теплоенергетики пов'язане з виконанням законів України «Про енергозбереження» й «Про теплопостачання» і обумовлено використанням електроенергії власного виробництва, що значно дешевше мережної електроенергії. Когенераційні установки так само знижують навантаження на навколишнє середовище, знижуючи викиди CO й NOx комунальних котелень на 20-30% [6].
Все це є спонукальним мотивом для розробки нових технологій, що забезпечують підвищення ефективності використання органічного палива. Одним зі шляхів ефективного використання первинного палива, є впровадження сучасних енергозберігаючих когенераційних технологій, де коефіцієнт використання теплоти палива досягає 80-90 % [1]. Структурна схема когенераційної установки представлена на рис. 1.
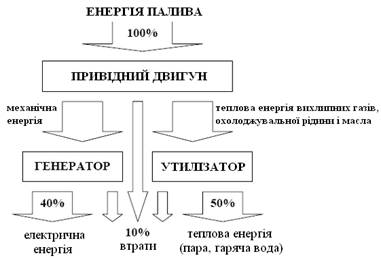
Рис. 1 Структурна схема когенераційної установки
Широкий розвиток одержало комбіноване виробництво електричної й теплової енергії на основі газотурбінних технологій [2]. Побудовано малі ТЕЦ (МТ) на природному газі для забезпечення електричною й тепловою енергією невеликих промислових підприємств, житлових районів міст і селищ.
Як газоподібне паливо можливе використання метану вугільного походження. Україна володіє величезними, фактично не розробленими, ресурсами метану вугільних родовищ. На території Донецького вугільного басейну запаси метану перевищують 14...22 трлн. кубометрів. Розрахунки фахівців і закордонна практика показують, що проблему ефективного використання шахтного метану вирішує застосування когенераційних технологій [3].
У наукових працях, присвячених дослідженню когенераційних енергетичних установок (КЕУ) [1,2,3,6] розглянуті деякі типи КЕУ й різні режими їхньої роботи в статиці. При створенні когенераційних установок, що працюють по нових циклах або нових схемах, з'являється необхідність у дослідженні динамічних процесів в установці при номінальному й частковому навантаженнях.
Розрахунки статики КЕУ показують високу економічність когенераційних установок при роботі в стаціонарних режимах. Але для вибору економічно оптимальної системи керування установкою при роботі на часткових навантаженнях, необхідно визначити динамічні характеристики й досліджувати перехідні процеси в системі при зовнішніх і внутрішніх збуреннях.
Для проведення досліджень динамічних властивостей КЕУ й варіантних досліджень схем регулювання потужності установки й схем стабілізації температури робочого тіла з метою вибору оптимальної системи регулювання необхідно побудувати математичну модель установки.
Аналіз досліджень і публікацій у цій області показав, що динамічні властивості подібного роду установок практично не вивчені. У роботі [7] представлена математична модель КЕУ, що може бути використана при аналізі динамічних характеристик когенераційної енергетичної установки з газовою турбіною у якості теплового двигуна.
Метою даної роботи є побудова математичної моделі водяного контуру теплопостачання когенераційної енергетичної установки, схема якої представлена на рис.2.
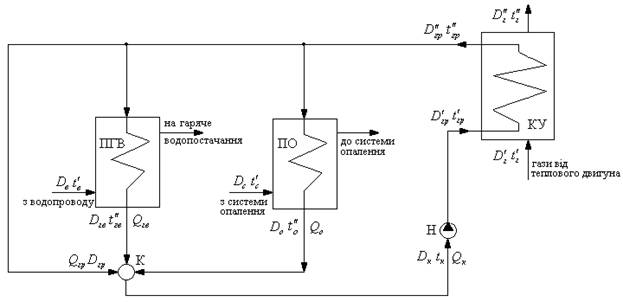
Рис. 2. Принципіальна схема контура теплопостачання КЕУ
Основними елементами схеми є: котел-утилізатор (КУ) заданої теплової потужності. Водо-водяні підігрівачі опалення (ПО) і гарячого водопостачання (ПГВ), зворотний колектор (К) і мережний насос (Н), що підтримує постійною витрату теплоносія в контурі.
Гази від теплового двигуна з температурою ![]() й витратою
й витратою ![]() надходять у котел-утилізатор і з температурою
надходять у котел-утилізатор і з температурою ![]() й витратою
й витратою ![]() залишають його. Теплоносій після мережного насоса з температурою
залишають його. Теплоносій після мережного насоса з температурою ![]() й витратою
й витратою ![]() нагрівається в КУ до температури
нагрівається в КУ до температури ![]() , і з витратою
, і з витратою ![]() направляється в підігрівачі ПО і ПГВ. У підігрівачах теплоносій нагріває воду із системи опалення до температури
направляється в підігрівачі ПО і ПГВ. У підігрівачах теплоносій нагріває воду із системи опалення до температури ![]() на потреби опалення й водопровідну воду до температури
на потреби опалення й водопровідну воду до температури ![]() для потреб гарячого водопостачання. Після чого через зворотний колектор і мережний насос із витратою
для потреб гарячого водопостачання. Після чого через зворотний колектор і мережний насос із витратою ![]() й температурою
й температурою ![]() повертається в котел-утилізатор.
повертається в котел-утилізатор.
Математична модель представляє собою систему диференціальних і алгебраїчних рівнянь, які наведені нижче.
Рівняння динаміки теплообмінника опалення:
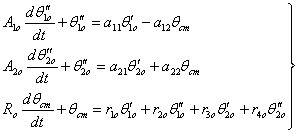 (1)
(1)
Рівняння динаміки теплообмінника гарячого водопостачання:
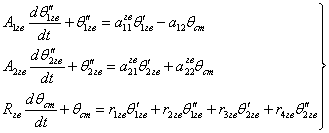 (2)
(2)
Рівняння динаміки котла-утилізатора:
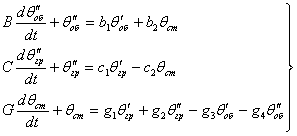 (3)
(3)
Рівняння зв’язку отримуємо з рівнянь теплового і матеріального балансів колектора:
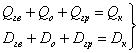 (4)
(4)
де ![]() – тепловий потік від підігрівача гарячого водопостачання, Дж/с;
– тепловий потік від підігрівача гарячого водопостачання, Дж/с;
![]() – тепловий потік від підігрівача опалення, Дж/с;
– тепловий потік від підігрівача опалення, Дж/с;
![]() – тепловий потік з гріючим середовищем перед колектором, Дж/с;
– тепловий потік з гріючим середовищем перед колектором, Дж/с;
![]() – тепловий потік після колектора, Дж/с;
– тепловий потік після колектора, Дж/с;
![]() – витрата гріючої води після ПГВ, кг/с;
– витрата гріючої води після ПГВ, кг/с;
![]() – витрата гріючої води після ПО, кг/с;
– витрата гріючої води після ПО, кг/с;
![]() – витрата гріючої води перед колектором, кг/с;
– витрата гріючої води перед колектором, кг/с;
![]() – витрата гріючої води після колектора, кг/с.
– витрата гріючої води після колектора, кг/с.
Витрата теплоносія в контурі не змінюється, тобто:
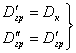 (5)
(5)
З рівнянь теплового і матеріального балансів отримуємо температуру на виході колектора:
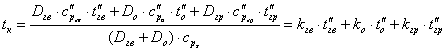 (6)
(6)
де 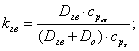
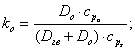
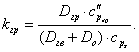
Вважаємо, що температура ![]() буде на вході насоса, тобто:
буде на вході насоса, тобто:
![]() (7)
(7)
де ![]()
Отримана таким чином математична модель контуру теплопостачання КЕУ, справедлива при малих відхиленнях від стаціонарного режиму й може бути ефективно використана для дослідження динаміки роботи контуру на часткових навантаженнях. А також, для дослідження впливу основних зовнішніх збурень: температура газів на вході до КУ ![]() , температура теплоносія на вході до КУ
, температура теплоносія на вході до КУ ![]() , температура зворотної води із системи опалення
, температура зворотної води із системи опалення ![]() на вході в ПО й температура води на вході в ПГВ
на вході в ПО й температура води на вході в ПГВ ![]() .
.
Література
1. Анализ эффективности интегрированных систем энергосбережения на базе установок когенерации малой мощности и возобновляемых источников энергии/Г.А. Баласанян, А.С. Мазуренко// Теплова енергетика. 2008. №1. С. 7-10.
2. Щаумов В.Ю. Опыт внедрения и эксплуатации ГТУ малой мощности.– В кн.: Малые и средние ТЭЦ. Современные решения. Тр. Конференции УМЦ «Голицино», 2005.
3. Когенерационные установки для утилизации шахтного метана / Богуслаев В.А. // Пром. теплотехника. 2009. №2, т. 31. С. 53-56.
4. Долінський А.А., Басок Б.І., Базєєв Е.Т., Пироженко І.А., колективна монографія. Комунальна теплоенергетика України: стан, проблеми, шляхи модернізації. – К.: т. 1-2. – 2007. – 828 с.
5. Програми технічної модернізації комунальної теплоенергетики регіонів України /Долінський А.А., Басок Б.І., Кучін Г.П., Базєєв Є.Т., Скрипко В.Я., Капустін В.Б., Чайка О.І.// Пром. теплотехника. 2009. № 1, Т.31. С. 5-14.
6. Энергетические и экологические показатели когенерационной установки электрической мощностью 1 МВт и тепловой мощностью 1,2 М.Вт./ Басок Б.И., Коломейко Д.А., Кужель Л.М.// Пром. теплотехника.2009. №2, т.31. С. 42-49.
7. Розробка математичної моделі динаміки когенераційної енергетичної установки.//Збірник наукових праць ОНАХТ. Одеса. 2009. С. 266-271.
Ответы на вопросы [_Задать вопроос_]
Читайте также
Моделирование объектов и систем управления
Соколов А.Е., Махова Е.О. Моделирование процесса принятия педагогического решения при компьютеризированном обученииСлавко О.Г. Порівняльний аналіз керування регулятором на основі локальної моделі керованого процесу та П-регулятором
Войтенко В.В., Дикусар Е.В, Ситников В.С. Определение частоты среза устройства сглаживания данных на основе метода скользящего среднего
Передерій В.І. Алгоритм визначення та оцінки характеристик ефективності комп’ютерних систем на початковій стадії проектування в умовах невизначенності
Ляшенко С.А, Ляшенко А.С. Оценка модели псевдолинейной регрессии
Ладієва Л.Р. Математична модель процесу газової мембранної дистиляції
Носов П.С., Косенко Ю.І. Нечіткі моделі і методи ідентифікації та прогнозу стану інформаційної моделі студента
Китаев А.В., Глухова В.И. Анализ работы синхронного двигателя с неявнополюсным ротором по данным каталога
Дорошкевич В.К., Пироженко А.В., Хитько А.В., Хорольский П.Г. К определению требований к системам увода космических объектов
Голінко І.М., Ковриго Ю.М., Кубрак А.І. Настройка системи керування за імпульсною характеристикою об’єкта
Яшина К.В., Садовой А.В. Комплексная математическая модель тепловых процессов, происходящих в дуговых электросталеплавильных печах
Шейник С.П., Рудакова А.В. Использование функций принадлежности для моделирования параметров распределенных объектов
Хомченко А.Н., Литвиненко Е.И. Метод барицентрического усреднения граничных потенциалов электростатического поля
Селяков Е. Б. Моделирование требований к техническим системам методами математической логики
Кириллов О.Л. , Якимчук Г.С. Моделирование процесса управления системой перегрузки углеводородных жидких топлив
Шеховцов А.Н., Козел В.Н. Построение математической модели формирования распределенных систем
Китаев А.В., Глухова В.И. Анализ поведения генератора постоянного тока по данным каталога
Хомченко А.Н., Козуб Н.О. Задачі наближення функцій: від лагранжевих до серендипових поліномів
Хобин В.А., Титлова О.А. Определение температуры парожидкостной смеси в дефлегматоре АДХМ по результатам измерений температуры его поверхности
Григорова Т.М., Усов А.В. Вероятностно-статистическое моделирование маршрутизированных пассажиропотоков в крупных городах
Горач О.О., Тернова Т.І. Моделювання технологічного процесу одержання трести при використані штучного зволоження з урахуванням складу мікрофлори
Дубік Р.М., Ладієва Л.Р. Математична модель розділення неоднорідних рідких систем
Казак В.М, Лейва Каналес Родриго, Яковицкая Е.Ю. Моделирование динамики полета магистрального самолета на исследовательском стенде
Завальнюк И.П. Исследование процесса торможения автомобиля как критического режима динамической системы
Дмитриев С.А., Попов А.В. Построение портрета неисправностей проточной части газотурбинного двигателя на примере АИ-25
Русанов С.А., Луняка К.В., Клюєв О.І., Глухов Г.М. Математичне моделювання робочого процесу в апаратах з віброкиплячим шаром та розробка систем автоматизованого моделювання гідродинаміки віброкиплячих шарів
Боярчук В.П., Сыс В.Б. Экспериментальные исследования влияния технологии шлихтования на изменение жесткости текстильных нитей
Селін Ю.М. Використовування контекстних марківських моделей для аналізу дії промислових вибухів на будівельні конструкції
Рудакова А.В. Проблемы интеграции сложных систем
Передерій В.І., Касап А.М. Математична модель та алгоритм автоматизації розрахунку параметрів комп’ютеризованих систем працюючих у реальному часі
Передерий В.И., Еременко А.П. Математические модели и алгоритмы принятия релевантных решений пользователями автоматизированных систем с учетом личностных и внешних факторов на базе генетических алгоритмов
Михайловская Т.В., Михалев А.И., Гуда А.И. Исследование правил клеточных автоматов для моделирования процессов затвердевания квазиравновесных бинарных сплавов
Хомченко А.Н., Колесникова Н.В. Явление «сверхсходимости» в задаче Прандтля для уравнения Пуассона
Китаев А.В., Глухова В.И. Анализ работы трансформатора по данным каталога
Квасницкий В.В., Ермолаев Г.В., Матвиенко М. В., Бугаенко Б.В., Квасницкий В.Ф. Оценка применимости метода компьютерного моделирования к исследованию напряженно-деформиррованного состояния цилиндрических узлов
Китаев А.И., Глухова В.И. Анализ работы асинхронного двигателя по данным каталога
Шелестов А.Ю Имитационная модель взаимодействия GRID-узлов с очередью доступа к общей памяти
Chizhenkova R.A. Mathematical Aspects of Bibliometrical Analysis of Neurophysiological Investigations of Action of Non-ionized Radiation (Medline-Internet)
Хомченко А.Н., Козуб Н.А. Геометрическое моделирование дискретных элементов с криволинейными границами
Славич В.П. Модель автоматизованої системи управління потоками транспортних засобів
Маркута О.В., Мысак В.Ф. Программная реализация и исследование особенностей метода группового учета аргументов
Степанкова Г.А., Баклан І.В. Побудова гібридних моделей на основі прихованих марківських моделей та нейронних мереж
Бакшанська Т.Д., Рижиков Ю.Г., Тодорцев Ю.К. Математична модель процесу горіння природного газу з рециркуляцією продуктів згорання для цілей управління
Хомченко А.Н. Новые решения обобщенной задачи Бюффона
Передерий В.И., Еременко А.П. Математические модели и алгоритмы определения релевантности принимаемых решений с учетом психофункциональных характеристик пользователей при управлении автоматизированными динамическими системами
Ложечников В.Ф., Михайленко В.С., Максименко И.Н. Аналитическая много режимная математическая модель динамики газовоздушного тракта барабанного котла средней мощности
Ковриго Ю.М., Фоменко Б.В., Полищук И.А. Математическое моделирование систем автоматического регулирования с учетом ограничений на управление в пакете Matlab
Исаев Е.А., Наговский Д.А. Математическое описание влияния кривизны контактирующих тел на угол смачивания жидкости в межчастичном пространстве
Бідюк П.І., Литвиненко В.І., Кроптя А.В. Аналіз ефективності функціонування мережі Байєса
Тищенко И.А., Лубяный В.З. Математическое моделирование вокодера для определения оптимальной формы импульса сигнала возбуждения.
Николаенко Ю.И., Моисеенко С.В. Моделирование гармонического полиномиального базиса гексагона.
Козуб Н.А., Манойленко Е.С., Хомченко А.Н. Температурный тест для модифицированных базисов бикубической интерполяции.
Клименко А.К. Об упрощенном численном конструировании обратной модели динамического объекта.
Китаев А.В., Сушич Е.Ф. Расчет погрешностей измерительных трансформаторов.
Передерій В.І.,Касап А.М. Математична модель та алгоритм автоматизації розрахунку параметрів комп’ютеризованих систем працюючих у реальному часі
Шпильовий Л.В. Математична модель та алгоритм екстремального управління процесом осадження дисперсної фази суспензії.
Тулученко Г.Я. Інформаційний модуль експрес-пошуку точок еквівалентності процесу нейтралізації.
Тернова Т.І. Урахування морфогенетичного рівняння в математичній моделі тканини.
Попруга А.Г. Теоретические и экспериментальные исследования электрических нагревателей по критерию экономии энергии.
Китаев А.В., Сушич Е.Ф. Приложение положений теории дросселя и трансформатора к расчету и анализу электромагнитом переменного тока.