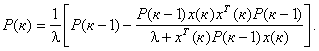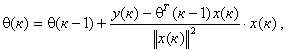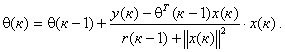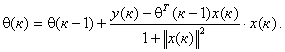УДК 519.71
ОЦЕНКА МОДЕЛИ ПСЕВДОЛИНЕЙНОЙ РЕГРЕССИИ
Введение. В производстве, относящемся к перерабатывающей отрасли свеклосахарного производства Украины, значительное место занимают вопросы эффективности производства. Эффективность производства заключается в получении наибольшего количества качественной производимой продукции (сахара, жома и т.д.), при одновременной минимизации расхода энергоресурсов (электричества, пара и т.д.) и использовании высокопроизводительного, безопасного оборудования и современных технологий.
Сахарное производство относится к сложным технологическим процессам, в котором участвуют большое количество разнообразного оборудования, работу которого необходимо контролировать с помощью автоматизированной системы управления технологическими процессами.
Так как в технологическом процессе получения сахара происходят сложные химические процессы, и имеется много производственных подразделения – диффузионное, дефекосатурационное, выпарное и кристаллизационное отделения, каждое из которых выполняет свои задачи в технологическом процессе, то объектом исследований является оборудование и производственные процессы, которые необходимо рассматривать как сложный динамический объект. Сложные динамические объекты характеризуются нелинейностью между входными и выходными параметрами в системе управления и нестационарностью процесса, так как в течение выполнения технологических операций происходит изменение параметров, а системе автоматизации необходимо контролировать и регулировать эти изменения в соответствии с требованиями технологии.
Для достижения поставленных целей используют в производстве автоматизированные системы управления технологическими процессами (АСУТП), которые и позволяют минимизировать затраты и получить наибольший выход продукции. Современные системы автоматизации, в зависимости от потребностей производства, бывают одно, двух или трехуровневыми. Первый уровень в системе автоматизации присутствует в любом случае, так как производство не может осуществляться без наличия оборудования и арматуры. АСУТП включают в себя наличие всевозможного измерительного оборудования (датчики, расходомеры, манометры и т.д.), регистрирующего оборудования (амперметры, вольтметры и т.д.), управляющей техники (контроллеры, компьютеры и т.д.), исполнительного оборудования (электро-пневмопозиционеры, клапаны, заслонки и т.д.), а также программного обеспечения.
В перерабатывающем сахарном производстве огромное значение имеет соблюдение технологических режимов получения сахарной продукции, которые заключаются в поддержании температурных режимов, при которых осуществляется переработка сахарной свеклы в свекольную стружку, диффузионный сок, сироп и сахар. Кроме температурного режима для перерабатываемой продукции необходимо поддерживать в необходимых режимных диапазонах рН, соотношения свекловодной смеси, СО, высоту выпариваемой жидкости и т.д.
Для поддержания этих режимов необходимо, чтобы завод мог обеспечить технологию получения сахара необходимыми энергоресурсами (электричество и ретурный пар), а также переработка сырья при помощи оборудование должна осуществляться при соответствующих режимах.
Для регулировки и поддержания необходимых технологических режимов в сахарном производстве необходимо уделить внимание вопросам управления автоматизированной системой технологических процессов. Управление невозможно без знания математической модели процесса.
Среди существующих систем автоматического управления в последнее время наиболее эффективными для этих целей подходят системы управления, базирующиеся на нейросетевом подходе.
Решение задачи оптимизации предполагает наличие математической модели исследуемого процесса. Если данный процесс является стационарным либо квазистационарным, построение модели осуществляется с помощью нерекуррентных методов, в которых одновременно используется вся информация о процессе. При этом важным является наличие априорной информации о его свойствах и о статических свойствах присутствующих возмущений и помех. Отсутствие такой информации, а также нелинейность и нестационарность реальных процессов обусловливает применение адаптивного подхода для построения математической модели исследуемого процесса, при котором сложная нелинейная модель заменяется линейной моделью с переменными параметрами, уточняемыми по мере поступления новой информации. Используемые при этом алгоритмы коррекции параметров основаны, как правило, на методе наименьших квадратов (МНК) и представляют собой обычно некоторую разновидность рекуррентного МНК, отличающегося от стандартного РМНК наличием механизма оценивания важности вновь поступающей информации (наиболее часто в качестве такого механизма используется экспоненциальное взвешивание информации). С другой стороны, достаточно эффективным, но значительно более простым в реализации является алгоритм Качмажа.
Цель работы. Целью данной работы является разработка и исследование алгоритма оценивания, сочетающего в себе свойства алгоритмов Качмажа и РМНК с экспоненциальным взвешиванием информации.
Постановка задачи. Рассмотрим задачу оценивания параметров модели псевдолинейной регрессии
|
|
(1) |
где ![]() - входной и выходной сигналы исследуемого процесса соответственно;
- входной и выходной сигналы исследуемого процесса соответственно; ![]() - подлежащий оцениванию вектор в общем случае нестационарных параметров;
- подлежащий оцениванию вектор в общем случае нестационарных параметров; ![]() - помеха измерения;
- помеха измерения; ![]() - дискретное время.
- дискретное время.
К виду (1) могут быть приведены различные уравнения, описывающие линейные и нелинейные процессы [1].
Использование в качестве минимизируемого функционала вида
|
|
(2) |
где
|
|
(3) |
![]() - оценка вектора параметров
- оценка вектора параметров ![]() ;
;
![]() - параметр взвешивания информации,
- параметр взвешивания информации,
приводит к РМНК с экспоненциальным взвешиванием информации
|
|
(4) |
|
|
(5) |
Следует отметить, что выбор параметра ![]() представляет собой сложную задачу, так как эффективность данного алгоритма существенно зависит от этого единственного свободно выбираемого параметра [1,2].
представляет собой сложную задачу, так как эффективность данного алгоритма существенно зависит от этого единственного свободно выбираемого параметра [1,2].
Наличие операции вычитания в (5) может привести к тому, что алгоритм (4) – (5) станет неустойчивым. С целью улучшения его вычислительных свойств в ряде работ предлагалась его регуляризация. Так в работе [3] изучалась модификация РНМК, регуляризация которой осуществлялась выбором соответствующих начальных значений матрицы ![]() . Такой подход обосновывается тем, что рекуррентная оценка МНК и нерекуррентная совпадают в асимптотике, поэтому выбор подходящих начальных условий играет определяющую роль. В работе [4] предлагался алгоритм РМНК, в котором используется следующая процедура вычисления матрицы
. Такой подход обосновывается тем, что рекуррентная оценка МНК и нерекуррентная совпадают в асимптотике, поэтому выбор подходящих начальных условий играет определяющую роль. В работе [4] предлагался алгоритм РМНК, в котором используется следующая процедура вычисления матрицы ![]() :
:
|
|
(6) |
где ![]() - величина, соизмеримая с минимальным собственным значением матрицы
- величина, соизмеримая с минимальным собственным значением матрицы ![]() ;
; ![]() ;
; ![]() - единичная матрица.
- единичная матрица.
Хотя введение матрицы ![]() и обеспечивает повышение вычислительной устойчивости процесса оценивания, вопрос о выборе оптимальных значений
и обеспечивает повышение вычислительной устойчивости процесса оценивания, вопрос о выборе оптимальных значений ![]() и
и ![]() остается открытым.
остается открытым.
Более простым и удобным в реализации является одношаговый алгоритм Качмажа [5]
|
|
(7) |
не использующий операцию обращения (рекуррентного вычисления) матрицы ![]() и являющийся более устойчивым по сравнению с (4) – (5). Однако если компоненты вектора
и являющийся более устойчивым по сравнению с (4) – (5). Однако если компоненты вектора ![]() находятся вблизи машинного нуля, то величина
находятся вблизи машинного нуля, то величина ![]() может оказаться равной нулю или иметь очень малую точность, т.е. оценка, вычисляемая в соответствии с (7) будет не устойчивой.
может оказаться равной нулю или иметь очень малую точность, т.е. оценка, вычисляемая в соответствии с (7) будет не устойчивой.
Промежуточное место между алгоритмами (7) и (4) – (5) занимает алгоритм предложенный в работе [6]
|
|
(8) |
и являющийся обобщением алгоритма [7]
|
|
(9) |
Здесь ![]() ;
; ![]() - евклидова норма.
- евклидова норма.
Рассмотрим алгоритм, сочетающий в себе свойства РМНК (4) – (5) и одношаговых алгоритмов (7) – (9).
Модифицированный алгоритм РМНК. Как видно из структуры алгоритмов, все они могут быть записаны в виде
|
|
(10) |
где ![]() - некоторый матричный или скалярный коэффициент усиления.
- некоторый матричный или скалярный коэффициент усиления.
Рассмотрим выбор матричного коэффициента в виде
|
|
(11) |
где ![]() - некоторая постоянная матрица;
- некоторая постоянная матрица; ![]() - матрица, аналогичная матрице, используемой в РМНК и вычисляемая следующим образом:
- матрица, аналогичная матрице, используемой в РМНК и вычисляемая следующим образом:
|
|
(12) |
Как следует из (12), алгоритмы (4) – (5), (7) – (9) получаются из (11) соответствующим выбором параметров ![]() и матрицы
и матрицы ![]() .
.
Запишем алгоритм (11) – (12) относительно ошибок оценивания ![]() . Для анализа сходимости алгоритма выберем функцию Ляпунова вида
. Для анализа сходимости алгоритма выберем функцию Ляпунова вида
|
|
(13) |
и рассмотрим ее приращение
|
|
(14) |
Для сходимости алгоритма необходимо выполнение условия
|
|
(15) |
|
|
|
Подставив в (14) выражение для ![]() из (10) и приведя подобные, получим
из (10) и приведя подобные, получим
![]()
где ![]()
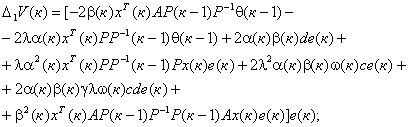
![]()
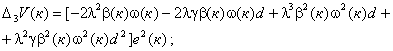
![]()
![]()
![]()
![]()
После несложных, но громоздких преобразований можно получить, что алгоритм (11)-(12) сходится, т.е. неравенство (15) выполняется, если
|
|
(16) |
|
|
(17) |
Из (16), (17) видно, что параметры ![]() и
и ![]() являются функциями времени и могут быть без труда вычислены, так как все входящие в данные условия величины либо известны (
являются функциями времени и могут быть без труда вычислены, так как все входящие в данные условия величины либо известны (![]() и
и ![]() ), либо легко определяются
), либо легко определяются ![]() . Оптимальные же значения этих параметров могут быть получены путём решения дополнительной оптимизационной задачи.
. Оптимальные же значения этих параметров могут быть получены путём решения дополнительной оптимизационной задачи.
Выводы. В статье предложена и исследована модификация рекуррентного алгоритма МНК, представляющая собой комбинацию РМНК и алгоритма Гудвина-Ремеджа-Кейнеса. По аналогии с РМНК данный алгоритм обладает хорошими фильтрующими свойствами, а использование в нем дополнительной положительно определённой матрицы обеспечивает устойчивость процесса оценивания.
С целью обеспечения наибольшей скорости сходимости данного алгоритма, используемые в нем параметры ![]() и
и ![]() должны быть выбраны путём, например, минимизации функционала (13). Однако, как нетрудно заметить, получаемые при этом оптимальные значения этих параметров будут зависеть от наличия априорной информации о свойствах полезных сигналов и помех. Поэтому при практическом применении данного алгоритма следует пользоваться оценками этих параметров, получаемыми с помощью соответствующих рекуррентных алгоритмов.
должны быть выбраны путём, например, минимизации функционала (13). Однако, как нетрудно заметить, получаемые при этом оптимальные значения этих параметров будут зависеть от наличия априорной информации о свойствах полезных сигналов и помех. Поэтому при практическом применении данного алгоритма следует пользоваться оценками этих параметров, получаемыми с помощью соответствующих рекуррентных алгоритмов.
ЛИТЕРАТУРА.
1. Эйкхофф П. Основы идентификации систем управления. – М.: Мир, 1975. – 683с.
2. Изерман Р. Цифровые системы управления. – М.: Мир, 1984. – 541с.
3. Жуковский Е.Л., Липцер Р.Ш. О рекуррентном способе вычисления нормальных решений линейных алгебраических уравнений // Журнал вычислительной математики и математической физики. – 1982. – Т. 12. - №4. – с. 843-857.
4. Salgado M.E., Goodwin G.C, Middleton R.H. Modified least squares algorithm incorporating exponential resetting and forgetting // Int. J. Control. – 1988. – Vol. 47. - №2. – Р.477 – 491.
5. Райбман Н.С., Чадеев В.М. Построение моделей процессов производства. – М.: Энергия, 1975. – 375с.
6. Goodwin G.C., Ramadge P.J., Caines P.E. Discrete time multivariable adaptive control // IEEE Trans. Aut. Control. - 1978. - Vol. AC-25. - №2. – Р.449 – 456.
7. Goodwin G.C., Sin K.S. Adaptive filtering prediction and control. - Englewood Cliffs, New Jersey: Prentice Hall, 1984. – 540p.
Ответы на вопросы [_Задать вопроос_]
Читайте также
Моделирование объектов и систем управления
Соколов А.Е., Махова Е.О. Моделирование процесса принятия педагогического решения при компьютеризированном обученииСлавко О.Г. Порівняльний аналіз керування регулятором на основі локальної моделі керованого процесу та П-регулятором
Войтенко В.В., Дикусар Е.В, Ситников В.С. Определение частоты среза устройства сглаживания данных на основе метода скользящего среднего
Передерій В.І. Алгоритм визначення та оцінки характеристик ефективності комп’ютерних систем на початковій стадії проектування в умовах невизначенності
Ладієва Л.Р. Математична модель процесу газової мембранної дистиляції
Носов П.С., Косенко Ю.І. Нечіткі моделі і методи ідентифікації та прогнозу стану інформаційної моделі студента
Китаев А.В., Глухова В.И. Анализ работы синхронного двигателя с неявнополюсным ротором по данным каталога
Дорошкевич В.К., Пироженко А.В., Хитько А.В., Хорольский П.Г. К определению требований к системам увода космических объектов
Голінко І.М., Ковриго Ю.М., Кубрак А.І. Настройка системи керування за імпульсною характеристикою об’єкта
Яшина К.В., Садовой А.В. Комплексная математическая модель тепловых процессов, происходящих в дуговых электросталеплавильных печах
Шейник С.П., Рудакова А.В. Использование функций принадлежности для моделирования параметров распределенных объектов
Хомченко А.Н., Литвиненко Е.И. Метод барицентрического усреднения граничных потенциалов электростатического поля
Селяков Е. Б. Моделирование требований к техническим системам методами математической логики
Тодорцев Ю.К., Ларіонова О.С., Бундюк А.М. Математична модель контура теплопостачання когенераційної енергетичної установки
Кириллов О.Л. , Якимчук Г.С. Моделирование процесса управления системой перегрузки углеводородных жидких топлив
Шеховцов А.Н., Козел В.Н. Построение математической модели формирования распределенных систем
Китаев А.В., Глухова В.И. Анализ поведения генератора постоянного тока по данным каталога
Хомченко А.Н., Козуб Н.О. Задачі наближення функцій: від лагранжевих до серендипових поліномів
Хобин В.А., Титлова О.А. Определение температуры парожидкостной смеси в дефлегматоре АДХМ по результатам измерений температуры его поверхности
Григорова Т.М., Усов А.В. Вероятностно-статистическое моделирование маршрутизированных пассажиропотоков в крупных городах
Горач О.О., Тернова Т.І. Моделювання технологічного процесу одержання трести при використані штучного зволоження з урахуванням складу мікрофлори
Дубік Р.М., Ладієва Л.Р. Математична модель розділення неоднорідних рідких систем
Казак В.М, Лейва Каналес Родриго, Яковицкая Е.Ю. Моделирование динамики полета магистрального самолета на исследовательском стенде
Завальнюк И.П. Исследование процесса торможения автомобиля как критического режима динамической системы
Дмитриев С.А., Попов А.В. Построение портрета неисправностей проточной части газотурбинного двигателя на примере АИ-25
Русанов С.А., Луняка К.В., Клюєв О.І., Глухов Г.М. Математичне моделювання робочого процесу в апаратах з віброкиплячим шаром та розробка систем автоматизованого моделювання гідродинаміки віброкиплячих шарів
Боярчук В.П., Сыс В.Б. Экспериментальные исследования влияния технологии шлихтования на изменение жесткости текстильных нитей
Селін Ю.М. Використовування контекстних марківських моделей для аналізу дії промислових вибухів на будівельні конструкції
Рудакова А.В. Проблемы интеграции сложных систем
Передерій В.І., Касап А.М. Математична модель та алгоритм автоматизації розрахунку параметрів комп’ютеризованих систем працюючих у реальному часі
Передерий В.И., Еременко А.П. Математические модели и алгоритмы принятия релевантных решений пользователями автоматизированных систем с учетом личностных и внешних факторов на базе генетических алгоритмов
Михайловская Т.В., Михалев А.И., Гуда А.И. Исследование правил клеточных автоматов для моделирования процессов затвердевания квазиравновесных бинарных сплавов
Хомченко А.Н., Колесникова Н.В. Явление «сверхсходимости» в задаче Прандтля для уравнения Пуассона
Китаев А.В., Глухова В.И. Анализ работы трансформатора по данным каталога
Квасницкий В.В., Ермолаев Г.В., Матвиенко М. В., Бугаенко Б.В., Квасницкий В.Ф. Оценка применимости метода компьютерного моделирования к исследованию напряженно-деформиррованного состояния цилиндрических узлов
Китаев А.И., Глухова В.И. Анализ работы асинхронного двигателя по данным каталога
Шелестов А.Ю Имитационная модель взаимодействия GRID-узлов с очередью доступа к общей памяти
Chizhenkova R.A. Mathematical Aspects of Bibliometrical Analysis of Neurophysiological Investigations of Action of Non-ionized Radiation (Medline-Internet)
Хомченко А.Н., Козуб Н.А. Геометрическое моделирование дискретных элементов с криволинейными границами
Славич В.П. Модель автоматизованої системи управління потоками транспортних засобів
Маркута О.В., Мысак В.Ф. Программная реализация и исследование особенностей метода группового учета аргументов
Степанкова Г.А., Баклан І.В. Побудова гібридних моделей на основі прихованих марківських моделей та нейронних мереж
Бакшанська Т.Д., Рижиков Ю.Г., Тодорцев Ю.К. Математична модель процесу горіння природного газу з рециркуляцією продуктів згорання для цілей управління
Хомченко А.Н. Новые решения обобщенной задачи Бюффона
Передерий В.И., Еременко А.П. Математические модели и алгоритмы определения релевантности принимаемых решений с учетом психофункциональных характеристик пользователей при управлении автоматизированными динамическими системами
Ложечников В.Ф., Михайленко В.С., Максименко И.Н. Аналитическая много режимная математическая модель динамики газовоздушного тракта барабанного котла средней мощности
Ковриго Ю.М., Фоменко Б.В., Полищук И.А. Математическое моделирование систем автоматического регулирования с учетом ограничений на управление в пакете Matlab
Исаев Е.А., Наговский Д.А. Математическое описание влияния кривизны контактирующих тел на угол смачивания жидкости в межчастичном пространстве
Бідюк П.І., Литвиненко В.І., Кроптя А.В. Аналіз ефективності функціонування мережі Байєса
Тищенко И.А., Лубяный В.З. Математическое моделирование вокодера для определения оптимальной формы импульса сигнала возбуждения.
Николаенко Ю.И., Моисеенко С.В. Моделирование гармонического полиномиального базиса гексагона.
Козуб Н.А., Манойленко Е.С., Хомченко А.Н. Температурный тест для модифицированных базисов бикубической интерполяции.
Клименко А.К. Об упрощенном численном конструировании обратной модели динамического объекта.
Китаев А.В., Сушич Е.Ф. Расчет погрешностей измерительных трансформаторов.
Передерій В.І.,Касап А.М. Математична модель та алгоритм автоматизації розрахунку параметрів комп’ютеризованих систем працюючих у реальному часі
Шпильовий Л.В. Математична модель та алгоритм екстремального управління процесом осадження дисперсної фази суспензії.
Тулученко Г.Я. Інформаційний модуль експрес-пошуку точок еквівалентності процесу нейтралізації.
Тернова Т.І. Урахування морфогенетичного рівняння в математичній моделі тканини.
Попруга А.Г. Теоретические и экспериментальные исследования электрических нагревателей по критерию экономии энергии.
Китаев А.В., Сушич Е.Ф. Приложение положений теории дросселя и трансформатора к расчету и анализу электромагнитом переменного тока.