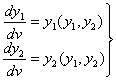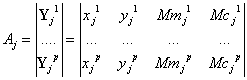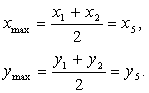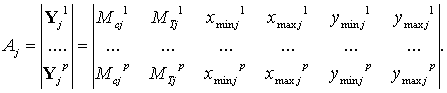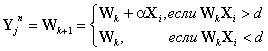Автоматика.
    Автоматизация.
        Электротехнические
            комплексы и системы.

УДК 677.019

АЛГОРИТМ  ОБУЧЕНИЯ  СИСТЕМЫ  РАСПОЗНАВАНИЯ АВТОМАТИЧЕСКОЙ   СИСТЕМЫ  РАЗБРАКОВКИ  ТКАНЕЙ

Рожков С.А., Федотова О.Н.

Решение вопросов автоматизации контроля качества текстильных материалов (тканей) с использованием телевизионных систем сдерживается из-за проблемы создания таких систем контроля, которые  могли бы  обнаруживать  и распознавать дефекты (пороки) тканей с малыми уровнями соотношения сигнал-шум [1, 4].

Необходимость разработки специальных методов и средств обнаружения сигналов дефектов, значительные  потоки  информации в системах обработки сигналов, отсутствие приемников излучения фотоэлектрического типа с  необходимыми кривыми спектральной чувствительности и  высокая стоимость известных систем контроля качества – это факторы, которые сдерживают создание и широкое внедрение таких систем автоматической  разбраковки  тканей [1, 2].

Кроме того, дефекты тканей отражают нарушения технологических режимов производства и  своевременный анализ полного потока дефектов позволяет повысить эффективность производства тканей [3, 4].

Система распознавания дефектов ткани разрабатывается как часть АСУТП разбраковки тканей, при этом  необходимо  разработать классификатор системы, который будет  осуществлять распознавание дефектов тканей согласно ГОСТ 161-86 [5].

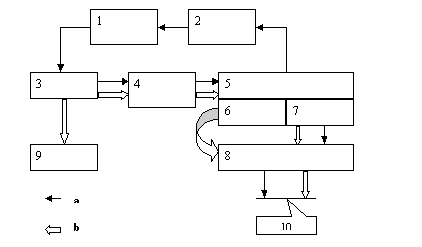
Структурная схема обучающейся системы распознавания представлена на рис.1.

 

Рис.1  Структурная схема системы распознавания с обучением 1 – обучающие объекты, 2 – учитель,  3- детектор признаков, 4 – система обработки информации, 5 – память, 6- эталонное пространство, 7-алгоритм обучения, 8 – классификатор, 9- распознаваемые объекты, 10 – решение, а – режим работы, b – режим обучения.

 

В системах без обучения количества первоначальной информации достаточно для того, чтобы определить словарь признаков, описать каждый класс объектов на языке этих признаков и в соответствии с выбранным принципом классификации разделить все множество объектов на классы.

В обучающихся системах распознавания обычно недостаточно информации для описания классов на языке выбранных признаков, но характер априорной информации позволяет различать принадлежность конкретных объектов соответствующим классам и организовать процедуру обучения.

В самообучающихся системах количество первоначальной априорной информации достаточно только для определения словаря признаков и нет никаких указаний о принадлежности объектов к какому-то классу. Эти указания заменяются наборами правил, в соответствии с которыми на стадии самообучения система распознавания сама вырабатывает некоторую классификацию и в дальнейшем ее придерживается.

В зависимости от того, на языке каких признаков производится описание распознаваемых объектов - детерминированных, логических, стохастических, структурных или тех и других, системы распознавания могут быть подразделены на детерминированные, логические, вероятностные, структурные и комбинированные [6].

При формировании разделяющей границы между двумя классами C1 и С2 априорное распределение объектов классов чаще всего неизвестно, т.е. определить разделяющую границу расчетным путем не представляется возможным. Так как классы объединяют объекты, отличающиеся друг от друга по значимым признакам, то между двумя классами должна существовать разделяющая граница F(X1,X2), которая отображается решающей функцией F(Y1,Y2) в пространстве признаков эталонов разделяемых классов, где Y1, Y2 – вектора эталонов классов C1 и С2 соответственно.

Функция F(Y1,Y2) формируется в процессе обучения и представляет показатель качества распознавания, например, вероятность ошибки.

Предположив, что пошаговое изменение векторов эталонов будет незначительно изменять вероятность распознавания:

 

(1)

 

где t - любой параметр, который пошагово изменяет состояние системы.

Учитывая, что в структурной схеме системы распознавания с обучением имеется звено "оператор-учитель" и учитель обладает достаточной «квалификацией», то для того, чтобы осуществлять эффективное обучение с минимизацией ошибочного распознавания, целесообразно использовать (2) вместо (1):

 

(2)

 

В этом случае получаем возможность рассматривать задачу обучения как задачу оптимального управления системой по отношению к модели, что дает уравнение ошибки в виде

 

(3)

 

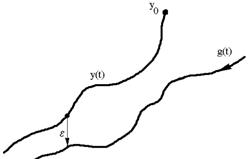
В новой системе координат (рис.2) согласно условию (3) траектории g(t) соответствует точка e=0, которая для  (3) является положением равновесия, так как F(0,t)=0.Таким образом, задача об устойчивости траектории g(t) сводится к задаче об устойчивости начала координат в пространстве измененных переменных [4].

Автоматическую систему разбраковки в режиме обучения можно отнести к автономным системам, так как движение разделяющей границы происходит не во времени, а по мере обработки очередного изображения обучающей выборки под воздействием оператора-учителя, который участвует непосредственно в работе системы.

Рис. 2  Траектория движения системы

 

Предположим,  что  система распознавания описывается системой второго порядка, т.е. распознавание проводится по двум значимым признакам:

 

(4)

 

где v - объем изображений обучающей выборки C₁ и С₂.

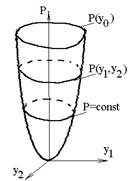
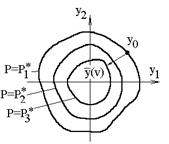
Пусть существует некоторая функция переменных состояний P(y₁,y₂) (рис.3,а), которая положительна всюду за исключением начала координат, где она равна 0.

Для системы распознавания в процессе обучения такой функцией является функция изменения вероятности ложного распознавания, которая в результате процедуры обучения должна быть либо минимальной, либо сведена к нулю. Другими словами, обучение может быть описано как движение системы по траектории y(v) (рис.3, б):

 

а)	б)
Рис. 3  Движение траектории y(v) в процессе обучения а) поверхность, определяющая функцию, б) проекции сечений функции P(Y1,Y2) плоскостями P=const.

 

Если  выполняется условие оптимальности, то траектория y(v) будет стремиться к началу координат. Но такое изменение траектории y(v) к началу координат не обязательно обеспечивает асимптотическую устойчивость, так как вблизи т.0,0 может наблюдаться dP/dv=0, (т.е. P=const), но при P=min простая устойчивость должна достигаться. Оценкой Р, характеризующей состояние системы распознавания, служит величина вероятности ошибочного распознавания на каждом шаге движения.

Требование оптимальности процесса обучения [7] приводит к традиционно используемому в данных задачах методу динамического программирования, который применяется для получения оптимальной траектории движения или оптимального управления, т.е. при  обеспечении минимального приращения траектории.

В процессе обучения распознающей системы необходимо сформировать такое эталонное пространство, которое бы отражало объекты обучающего массива W для последующей процедуры распознавания.

Для этого создана обучающая выборка, которая  получена из зафиксированных на ОАО «Херсонский ХБК» в течение 2-х лет дефектов тканей (размер исходного массива пороков примерно 20000) и количественно составила 984 объекта.

Анализ этих дефектов по причине их возникновения позволяет  выделить несколько  групп:

-        дефекты, обусловленные организацией технологического процесса, например, разный номер утка, шов;

-        дефекты процессов отбелки и аппретирования, например, плохая белизна;

-        дефекты процессов прядения и ткачества, например, слет по утку, утолщенная нить;

-        дефекты из-за несоответствия качества исходного продукта виду обрабатывающего агрегата и т.п.

Возникновение дефектов носит случайный характер, так как они обусловлены возможными случайными отклонениями в организации технологических процессов, естественными процессами старения оборудования и некомпетентностью обслуживающего персонала.

Для группы отбеленных и гладкокрашеных тканей согласно [5] можно выделить 16 классов (C_i) дефектов:

 

 

Разобьем множество изображений обучающего массива W на подмножества (классы) C1, С2, ... Сk такие, что:

 

 

где k- количество выделенных классов.

Для каждого изображения обучающей выборки указана его принадлежность определенному классу (образу). Каждое изображение обучающей выборки является реальным изображением, т.е. получено в условиях естественной зашумленности, и характеризуется вектором X.

В процессе формирования эталона на основе реальных изображений необходимо получить представление об идеальном образе класса и согласно последнему сформировать параметры эталона.

Процесс формирования эталонов можно представить следующим образом [9]:

 

(5)

 

где  – эталон j-го образа, элемент множества эталонов Y; множество Y состоит из подмножеств Y₁,...,Y_k таких, что в каждом из подмножеств содержится один и только один эталон. Понятие эталона вводится достаточно условно, так как в качестве исходного эталона может быть выбрано любое изображение, относящееся к данному классу, которое можно затем преобразовать;

 – реальное изображение дефекта на поле сканирования, принадлежит множеству изображений X_j, характеризующих класс С_j обучающего массива W;

 –  идеальное (без учета шума) изображение i-ro объекта j-ro образа на поле сканирования, принадлежит множеству идеальных изображений ;

z – шум, возникающий в процессе отображения;

 – функция, характеризующая воздействие шума;

 – функция отображения множества X на множество объектов наблюдения Y*, т.е. функция порождения объектов наблюдений;

β - мешающий переменный параметр отображения, характеризующий неопределенность, имеющую место при отображении объектов наблюдения;

 – функция отображения множества Y* на множество эталонов Y, т.е. функция порождения эталонов;

 –  i-ый объект наблюдения j-ro образа (принадлежит множеству ), сформированный на основе идеального изображения i-ro объекта j-ro образа :

 

 

В общем случае при обучении необходимо определить множество преобразований G, соответствующее множеству возможных изменений параметра β. Удобно формировать максимальный инвариант  [8] относительно параметра β по всем j и строить решающую функцию F(X), зависящую от X только через найденный максимальный инвариант.

В автоматической сканирующей системе разбраковки дефекты, проходящие в поле сканирования, на входе в блок обучения характеризуются вектором:

 

Х=(у,х,Мт,Мс),

(6)

           

где       у – длина дефекта, х - ширина дефекта, (у и х могут быть положительными и отрицательными величинами),

Мт – признак топологии (имеет 20 дискретных уровней),

Мс – признак сигнала (имеет 7 дискретных уровней).

Естественно, что множество эталонов Y должно формироваться в пространстве этих же координат. Но поскольку признаки Мт и Мс имеют по несколько дискретных уровней, исходное 4-хмерное эталонное пространство значительно расширяется:

 

 

Полученная размерность эталонного пространства характеризует общий случай, когда имеют место все значения признаков Мт и Мс.

Разделив множество входных объектов X_i по параметру , что в этом случае автоматически учитывает функция максимального инварианта Тβ(Х).

Таким образом, задача обучения в данном случае сводится к формированию разделяющих границ произвольного вида F(Y) между классами, в том числе пересекающимися, методом "прямоугольников" в эталонном пространстве, структуру которого можно определить следующим образом.

Вектор дефекта X согласно (6) имеет размерность:

 

 

Таким образом, структура эталонного пространства описывается выражением:

 

(7)

 

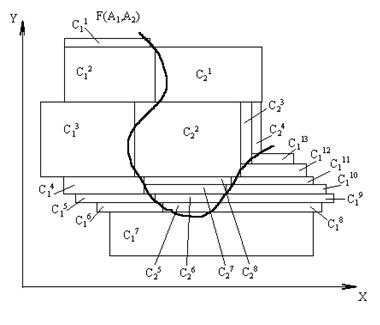
На рис. 4 показана разделяющая классы C₁ и С₂ граница F(A₁,A₂), построенная методом "четырехугольников", каждый из которых характеризует подкласс C_jⁿ (j= l,2 - количество классов, n=1...р, р - количество подклассов, A₁,A₂ - матрицы эталонов классов C₁ и С₂ соответственно).

 

Рис. 4  Разделяющая граница F(A1,A2) между пересекающимися классами C1 и С2

 

Матрица класса C_j A_j представляет собой матрицу-столбец, элементами которой являются вектора эталонов Y_jⁿ p подклассов данного класса Cj:

 

(8)

 

Здесь  характеризуют геометрические размеры пространственной области  , т.е. матрица А_j  описана через параметры эталонных областей. Класс дефектов включает все одноименные подклассы

 

(9)

 

Для рис.4:

 

 

Количество подклассов в каждом классе неограниченно. В области с меньшим градиентом разделяющей функции количество подклассов меньше (рис.4).  И наоборот, когда градиент разделяющей функции увеличивается, необходимо формировать большее количество подклассов, чтобы получить границу с минимальной ошибкой линейной аппроксимации.

Эталонная область каждого подкласса C_jⁿ строится в процессе итерационной процедуры из произвольной точки, которая определяется вектором первого дефекта данного подкласса.

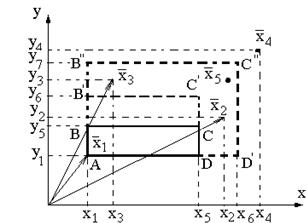
На рис.5 показан процесс формирования эталонной области Y произвольного подкласса в пространстве непрерывных параметров х и  у.

 

Рис.5  Формирование эталонной области подкласса при помощи обучающей выборки , формирование максимального  инварианта

 

Первый дефект подкласса, характеризующийся векторам X₁(x₁,y₁) формирует весовой вектор W₁ будущего эталона Y классификатора в виде:

 

 

т.е. формирует точку А, с которой начинается построение.

Второй дефект данного подкласса Х₂(х₂,У₂) преобразовывает точку А в эталонное пространство ABCD. При этом нижние границы области остаются без изменения:

Верхние границы эталонной области формируются методом половинного деления, который применяется достаточно часто, чтобы создать некоторую инерционность движения и не пропустить точку оптимума при движении к ней:

 

 

Весовой вектор W₂   области ABCD  будет иметь вид:

 

 

Дефект этого же подкласса Х₃(х₃,У₃) трансформирует пространство ABCD в AB'C'D. При этом координаты будущего вектора эталона изменяются:

 

т.е. изменилась только одна граница эталонной области - y_max :

 

 

При обработке дефекта Х₄ эталонная область расширяется до размеров АВ''С''D'. При этом весовой вектор подкласса корректируется:

 

 

Если следующим появляется дефект X₅, то корректировки вектора эталона не потребуется.

Таким образом, процесс обучения формирует такую эталонную область (вектор эталона Y_jⁿ), которая с каждым шагом формирования включает в себя все большее количество дефектов данного класса (подкласса).

Если данный класс не является смежным, процесс обучения заканчивается включением в параметры эталона дефектов, которые находятся за границами.  Их может быть только два:

 

 

где k - последний шаг обучения.

При этом сформированный вектор эталона  является максимальным инвариантом Tβ(X) относительно тех изображе­ний, которые присутствовали в обучающей выборке, и предполагает­ся, что максимальный инвариант сохраняется относительно изобра­жений данного подкласса, отсутствующих в данной выборке.

Учет дискретных параметров Мт и Mc изображения X_i не изменяет пространственной составляющей эталона, но трансформирует эталон­ную R⁴ - область в другую точку R¹⁴² - эталонного пространства.

Таким образом, в процессе обучения формируется эталон:

 

(10)

 

Если матрицу эталонов для класса C_j (8) представить через вектора эталонов (10), получим:

 

(11)

 

Так как весовой вектор корректируется в зависимости от векто­ра входного дефекта X_i, правило формирования вектора эталонной области Y_jⁿ  можно представить в виде:

 

(12)

 

где       k - номер шага обучения,

d - решение принадлежности дефекта X_i вектору W_k,

α - коэффициент приращения, может быть меньше нуля, так как при формировании эталонных областей пересекающих­ся классов возникает необходимость уменьшения эталон­ной области при возникновении ошибок первого рода, которые обнаруживаются при проверке вероятности рас­познавания.

Если в процессе распознавания i-ый объект наблюдения j-ro образа Y_ij^*, сформированный согласно (5) на основе изображения объекта в поле сканирования X_ij (6) не соответствует зависимости  т.е. на данный момент функционирования системы распознавания не сформирован эталон j-ro образа Y_j, по которому была бы возможна классификация объекта Y^*_ij, следует дообучить систему распознавания.

Если на вход распознающей системы поступил дефект нового класса C_k, в режиме обучения формируется весовой вектор первого приближения эталона Y_k, при этом список эталонов классификатора дополняется названием дефекта класса C_k.

Если принять во внимание, что при помощи обучающего алгоритма (12) в соответствии с правилом построения эталонов класса че­рез подклассы (9) формируется кусочно-линейная разделяющая граница между пересекающимися классами С₁ и С₂ (рис.4.4.1), то решающее правило запишется следующим образом:

 

(13)

 

Здесь Y₁^j - элементы матрицы эталонов А1, включающей эталоны всех подклассов класса С₁,

Y₂^j - элементы матрицы эталонов А2, включающей эталоны всех подклассов класса С₂.

Таким образом, в процессе обучения формируются матрицы этало­нов подклассов (11). Сформированный вектор эталона соответствует максимальному инварианту Тβ(Х) данного подкласса C_jⁱ.

Выводы

Автоматическая система распознавания на этапе обучения является автономной, так как изменение ее состояния зависит от обработки последовательности изображений обучающей выборки при помощи оператора-учителя, участвующего в управлении.

Теория устойчивости Ляпунова позволяет ожидать эффективного формирования эталонной области при движении системы из произвольного начального состояния по формирующейся в процессе обучения траектории при условии, что функция вероятности ложного распознавания будет стремиться к минимуму в конечной точке траектории (или равна нулю).

Процедура формирования такой траектории хорошо осуществляется при использовании динамического программирования, когда каждый последующий шаг формирования решающей границы базируется на предыдущих и обеспечивает небольшое приращение траектории, которое для любого вида функции на заданном отрезке можно линеаризовать.

Отличием от традиционно применяемой процедуры динамического программирования является отсутствие заданных множеств возможных управлений и соответствующих им состояний системы, а оптимальность каждого шага движения, проверяется по значению функции цели, при этом  вероятность ложного распознавания должна уменьшаться.

 

 

1.                  Горелик А.Л., Гуревич И.Б.Скрипкин В.А. Современное состояние проблемы распознавания. -М.: Радио и связь, 1985.

2.                  Храпливый А.П., Рожков С.А., Терновая Т.И., Бражник Д.А. Использование метода компенсации информационных потоков при создании систем автоматического распознавания. //Автоматика. Автоматизация. Электротехнические комплексы и системы. - 1998,  №2.  С.93-100.

3.                  Автоматизированные системы контроля качества готовых тканей в отделочном производстве /Ю.А.Павлов и др.-М.: Легкая и пищевая промышленность, 1981.-264с.

4.                  Рожков С.О., Тернова Т.І., Єдинович М.Б. Проблеми автоматизованого розбракування тканин. Проблемы легкой и текстильной промышленности Украины –2004.  №2(9),  С. 204-211.

5.                  ГОСТ 161-86 "Ткани хлопчатобумажные, смешанные и из пряжи химических волокон. Определение сортности".

6.                  Системы технического зрения (принципиальные основы, аппаратное и математическое обеспечение)/А.Н. Писаревский, А.Ф. Чернявский, Г.К. Афанасьев и др.; Под общ. ред. А.Н. Писаревского, А.Ф. Чернявского. –Л.: Машиностроение, Ленингр. отд-ние, 1988. –424 с. 

7.                  Справочник по теории автоматического управления А.Г.Александров и др. М., Наука, 1987.-712с.,ил.

8.                  Храпливый А.П., Федотова О.Н., Терновая Т.И. Адаптивный алгоритм разбраковки тканей по дефектам внешнего вида. Друга українська конференція з автоматичного керування "Автоматика-95", том 5, Львов, 1995 г. С.92.

9.                  Васильев В.И. Распознающие системы. Справочник. -К.: Наукова думка, 1983.

10.              Бейтс Р., Мак-Доннелл М. Восстановление и реконструкция изображений: Пер. с англ. –М.:Мир, 1989. –336 с.