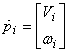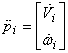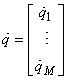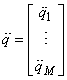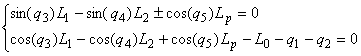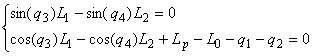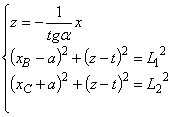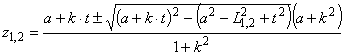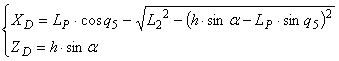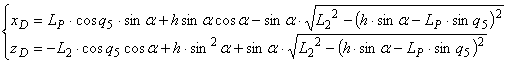УДК 621.9.06
ПРОГРАМНО‑МАТЕМАТИЧНИЙ АПАРАТ КЕРУВАННЯ ВИКОНАВЧИМ ОРГАНОМ БАГАТОКООРДИНАТНИХ ВЕРСТАТІВ НОВИХ КОМПОНОВОК
Кузнєцов Ю.М., Дмитрієв Д.О.
Постановка проблеми. Одним із перспективних напрямків багатономенклатурного серійного виробництва є створення програмно-керованого швидкопереналагоджувального технологічного обладнання, створеного на основі механізмів паралельної структури як принципово нового обладнання для виконання майже усіх технологічних операцій обробки, складання, випробування та вимірювання виробів [4, 5]. Концепція проектування технологічного обладнання з паралельною кінематикою [6] передбачає конструктивне виконання замкнених кінематичних ланцюгів у вигляді просторових стрижневих ферм. Усі кінематичні ланки механізму працюють одночасно (паралельно), що дозволяє виконавчому органу (ВО) верстату рухатись у просторі, забезпечуючи необхідний закон переміщення. Металообробні верстати з паралельною кінематикою мають більш широкий спектр технологічних можливостей ніж традиційні верстати внаслідок забезпечення виконавчому органу до шести ступенів вільності, що дозволяє йому здійснювати переміщення у просторі відносно усіх осей координатної системи та реалізувати майже усі схеми формоутворення поверхонь деталей, а також інші процеси виготовлення продукції за одну установку деталі з усіх сторін, крім базових. Серед сучасних комерційно запропонованих верстатів з паралельною кінематикою можна виділити дві основні групи: перша – просторові механізми з телескопічними штангами керовано-змінної довжини (біпод, трипод, пентапод, гексапод); друга – механізми з стрижнями постійної довжини, що шарнірно зв'язані з рухомими каретками, які розташовані на напрямних основи верстату (биглайд, тріаглайд, лінапод, гексаглайд) [2, 3]. Основним недоліком першої групи верстатів є те, що механізми приводів та крокові двигуни розташовані спільно з телескопічною штангою і місцем шарнірного з’єднання, і конструктивно складають єдиний рухомий вузол, що несе всі навантаження і погіршує динаміку верстату. На відміну від цього, в верстатах з штангами постійної довжини механізми приводів і двигуни розташовано на нерухомій основі (станині), а основне навантаження сприймається напрямними верстату. Дана обставина дозволяє зменшити рухомі маси стрижнів, забезпечити підвищені швидкості переміщень і прецизійність обробки.
Для поглибленого вивчення формоутворюючих рухів і створення нових компоновок верстатів з паралельною кінематикою необхідно мати наочний апарат моделювання багатоланкових замкнених кінематичних ланцюгів. Більшість сучасних САПР в останній час почали вводити окремі модулі для симуляції рухів кінематичних ланок і оцінки їх поведінки. Але ці методи мають стандартні інструменти прямої кінематики і обмежені застосуванням тільки для послідовних структур. Тому необхідно адаптувати алгоритми розрахунків положень ланок механізмів паралельної структури до умов процедурного і візуального програмування.
Мета дослідження. Виконати повузловий аналіз складових рухів механізмів паралельної структури із стрижнями постійної довжини з метою програмно-математичної реалізації комплексних формоутворюючих рухів верстатів з паралельною кінематикою в системах автоматизованого проектування і комп’ютерного моделювання.
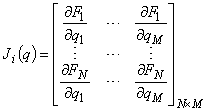
Аналіз попередніх досліджень. Аналіз прямої кінематики багатоланкових механізмів передбачає розв’язок системи алгебраїчних рівнянь F(q)=(f1(x1..., xn)...., fi(x1..., xn)), що описує трансформації локальних систем координат кожної ланки по відношенню до мирової системи відліку [7] або в системі координат верстату. Функція переміщень F(fi(x1..., xn)) вихідної ланки (виконавчого органу) буде безперервною, а відповідно диференціюватись по кожній з координаті в області визначення, якщо всі функції fi(x1..., xn) безперервні і диференціюються по кожній змінній (координаті) x1..., xn в області визначення. Умовою однозначного розв’язку системи рівнянь замкнених багатоланкових кінематичних ланцюгів буде
|
Fj(pi, q)=0 ( i=1, 2,..., K; j=1,2,..., N ) |
(1) |
де N – кількість ланок в замкненому кінематичному ланцюзі;
K – загальна кількість кінематичних ланцюгів в механізмі паралельної структури;
pi = [pi1, pi2,.... , piN,]T ,pi![]() RN змінні перетворень локальних систем координат кожної ланки в області визначень функції Fj ;
RN змінні перетворень локальних систем координат кожної ланки в області визначень функції Fj ;
q – множина керованих змінних q= [q1, q2,.... , qM,]T , що активують приводні ланки механізму в області значень функції Fj , q![]() RN.
RN.
Для отримання швидкостей і прискорень вихідної ланки механізму, що несе виконавчий орган верстату потрібно продиференціювати рівняння (1) в часних похідних по керованим змінним q.
|
|
|
де
|
|
(4) |
![]() ‑ якобіан (функціональний визначник) матриці M
‑ якобіан (функціональний визначник) матриці M![]() N для функції переміщень Fj
N для функції переміщень Fj
|
|
(5) |
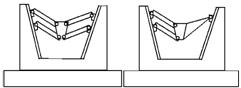
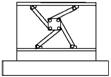
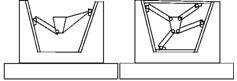
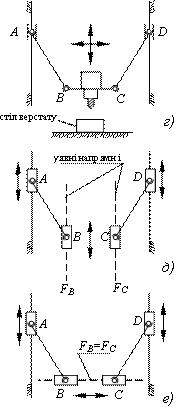
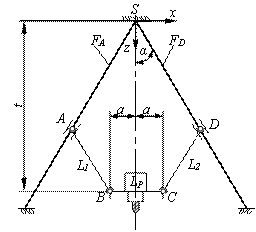
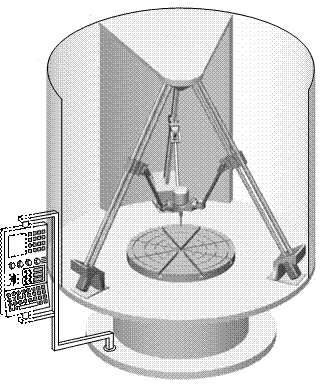
Механізми паралельної структури з ланками постійної довжини знайшли широке застосування в свердлильно-фрезерних верстатах. При збільшенні ступеня вільності ВО постає необхідність збільшувати кількість передавальних ланок, в наслідок чого зростають габарити і металоємність верстату (рис.1, рис.2). Крім того ускладнюється розрахунок кінематичних параметрів на етапі проектування компоновки верстату, а саме складання і диференціювання матриці (5).
Не складно помітити стремління різних розробників [8 ‑ 10] розташувати поступальніприводи кінців штанг співвісно один одному або на одній напрямній, що і визначає робочій простір верстату і форму станини. Так, верстат [8, 9] Hexaglide містить шість штанг і три напрямних (по дві штанги на кожній напрямній), а верстат Trijoint 900H має декілька модифікацій, але з аналогічною умовою (чотири штанги, дві напрямні). Це дозволяє виділити примітивний замкнений контур, що лежить в основі механізму біглайд і містить три зв’язані ланки, а саме, розташовані на повзунах дві штанги шарнірно зв’язані з вихідною ланкою, яка несе інструмент.
|
|
|
|
Рис.1 Фрезерний верстат Hexaglide розробники IWF і ETH (Швеція): а) – загальний вид; б) – конструктивна схема |
|
|
а) |
б) в) |
|
|
г) |
д) е) |
|
|
Рис.2 Свердлильно-фрезерний верстат Trijoint 900H [10]–а) та його модифікації – б, в, г, д, е |
||
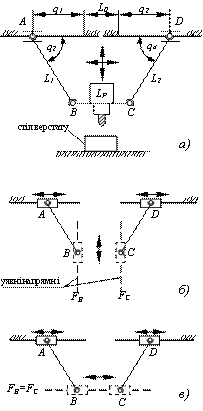
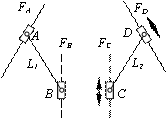
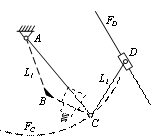
Основна частина. Розглянемо контур ABCD (рис.3,а). Система біглайду містить п’ять змінних:
q1 і q2, ‑ відстань опорного кінця штанги від крокового двигуна на напрямних верстату (активні змінні);
q3, q4, q5 – відповідно, кути нахилу ланок L1, L2 і LР до напрямних ( q5 на рис.3 не показано).
Зв’язок активних і пасивних змінних такого замкненого контуру буде
|
|
(6) |
Система (6) не має однозначного розв’язку, тому виключімо з неї змінну q5 і запишемо рівняння для поступального руху ВО уздовж координатних осей
|
|
(7) |
Продиференціював рівняння (7) отримаємо значення швидкостей ланок
|
|
(8) |
де 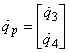 ‑ пасивні змінні,
‑ пасивні змінні, 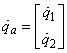 ‑ активні змінні;
‑ активні змінні;
функціональний визначник ‑ 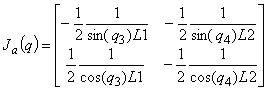 .
.
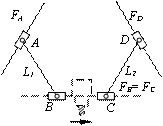
Виключимо умовно ланку ВС з замкненого контуру, але залишимо відстань між шарнірами В і С постійною і введемо уявні напрямні FC і FB , по яких відбувається їх рух (рис.3,б). В результаті отримаємо окремо пласкі механізми з повзунами, зв’язаними між собою шатуном, які рухаються синхронно.
|
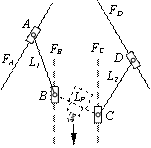
Рис.3 Декомпозиція механізму біглайд: а, б, в – горизонтальне розташування напрямних верстату; г, д, е ‑ вертикальне розташування напрямних верстату |
Даний механізм добре відомий як еліпсограф Леонардо да Вінчи [1], що реалізує еліптичний рух шатунної площини АВ(CD) . Очевидно, що при виключеній ланці ВС кількість і розташування напрямних не змінюють сутність механізму.
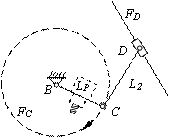
Змінимо кут напрямних верстату і зведемо їх в одну точку для збільшення жорсткості верстату та зниження довжини штанг (рис.4).
Для обчислення положень повзунів А і D при плоскопаралельному русі ВО складемо систему рівнянь
|
|
(9) |
Перше рівняння визначає розташування напрямної, інші кругову траєкторію, яку описують шатуни L1 і L2 навколо шарнірів при русі повзунів А і D по напрямним (рис.4, а).
Розв’язок системи (9) буде
|
|
(10)
(11) |
де ![]() .
.
|
а) |
б) |
|
Рис.4 Розрахункові схеми при а) ‑ плоскопаралельному і б) ‑ обертальному русі ланки ВС з інструментом для компоновки з кутовим розташування напрямних |
|
Обертальний рух вихідної ланки ВС обчислимо виключивши одну активну штангу, наприклад, ланку L1 і перенесемо центр обертання в точку В (рис.4, б). Положення повзуна D на напрямній в канонічній системі координат XOZ буде
|
|
(12) |
Задамо систему XOZ в точці В так, щоб вісь X була паралельна напрямній FD. Рівняння (12) в системі xBz прийме вид
|
|
(13) |
Розрахунок переміщень повзуна А по напрямній FA виконується аналогічно при виключенні ланки L1 і перенесенні центру обертання в точку С.
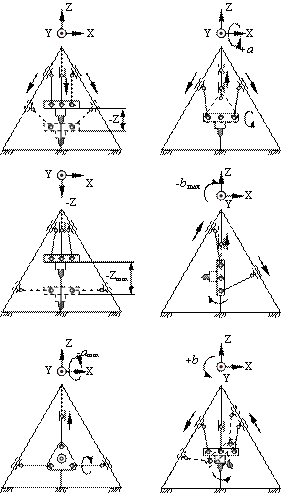
На основі трикутної форми розташування напрямних запропоновано [5] принципово нову пірамідальну компоновку і досліджено формоутворюючі рухи нового багатокоординатного свердлильно-фрезерного верстату підвищеної жорсткості (рис.5). Осі механізмів поступового руху мають одну точку перетинання, розташовану над платформою з інструментальним ВО, і утворюють правильну трикутну піраміду. Верстат має скорочену довжину штанг, три циліндричні напрямні і паралельно ним три кулькові гвинтові передачі з опорами на нижній основі. Напрямні упираються в підп'ятник закріплений на Г-подібній траверсі. Жорсткість пружної просторової рамної системи забезпечена конструктивним (форма виконання рамної системи), а не металоємним підвищенням опору поперечних перерізів кінематичних ланок і станини. В порівнянні об’ємів піраміди і призми однакової висоти і площею основи рамної системи виконання в пірамідальній компоновці втричі легше.
|
а) |
б) |
|
Рис.5 Багатокоординатний свердлильно-фрезерний верстат підвищеної жорсткості: а) – загальний вид; б) – основні технологічні рухи по керованим координатам |
|
В процесі комп'ютерного моделювання переміщень багатоланкового механізму необхідно визначити положення повзунів на напрямних верстату і орієнтацію штанг в світовій системі координат, коли ВО займає потрібне положення у просторі. Тобто треба вирішити обернену задачу кінематики. Рівняння замкненого векторного контуру (6) в багатоланковому механізмі з двома і більше активними змінними має складний розв’язок. Тому використаємо метод декомпозиції механізму і введемо уявні напрямні FВ , FС, по яким буде рухатись (ковзати) ланка LP , спираючись власними кінцями на уявні напрямні. Результати розкладання механізму на примітивні вузли по схемам керування (рис.4 і 5,б) наведено в табл.1. Отримані алгоритми реалізовано в тривимірному графічному середовищі 3DStudioMAX. Вибір програмного середовища обумовлено наявністю гнучкої об’єктно-орієнтованої мови програмування MaxScript суміщеної з графічним простором моделювання.
Створено інтерфейс програми, який дозволяє керувати положенням і орієнтацією ВО. Рухома платформа, місця з’єднання шарнірів, штанг з їх довжиною і положенням зв’язані змінними, математичними залежностями, що впливають на властивості об’єктів тривимірної моделі.
Таблица 1
Декомпозиція складових формоутворюючих рухів механізму паралельної структури з кутовим розташуванням напрямних
|
Схема руху виконавчого органу |
Взаємозв’язок змінних |
Схема руху виконавчого органу |
Взаємозв’язок змінних |
|
|
керовані змінні: ZB = ZC = t;
визначаються: ZA, ZD, XA, XD по формулам (10), (11) |
|
керовані змінні: q2 ;
сталі величини: ZA, XA; LP=AC
визначаються: ZD, XD по формулам (13). |
|
|
керовані змінні: XC ‑XB = ВС;
сталі величини: ВС=LP
визначаються: ZA, ZD, XA, XD по формулам (10), (11) |
|
керовані змінні: ZB = t;
сталі величини: q5=const ZC = sinq5 ·LP;
визначаються: ZA, ZD, XA, XD по формулам (10), (11) |
|
|
керовані змінні: q5 ;
сталі величини: ZA, XA, ZB, XB;
визначаються: ZD, XD по формулам (13). |
|
керовані змінні: ZB = t, XB = a;
сталі величини: q5, ZC = ZB + sinq5 ·LP, XC = XB + cosq5 ·LP;
визначаються: ZA, ZD, XA, XD по формулам (10), (11) |
|
|
керовані змінні: ZB , XB , q5
пасивні змінні: ZC = ZB + sinq5 ·LP, XC = XB + cosq5 ·LP;
визначаються: ZA, ZD, XA, XD по формулам (10), (11) |
|
керовані змінні: q4;
сталі величини: ZD, XD, ZC= ZB, q5 =0;
визначаються: ZA, ZD, XA, XD по формулам (10), (11) з підстановкою a=XB=cosq4·L2 + LP t = ZB = sinq4·L2 |
Висновки. Проведено аналіз складових формоутворюючих рухів механізмів паралельної структури зі штангами постійної довжини за допомогою умовного виключення однієї ланки і введенням уявних напрямних. В результаті визначено структуру примітивних вузлів замкнених кінематичних ланцюгів, отримано математичне описання рухів ланок на основі активних та пасивних змінних придатне для процедурного і об’єктно-орієнтованого програмування. Запропоновано нову компоновку багатокоординатного свердлильно-фрезерного верстату із кутовим розташуванням напрямних і досліджено переміщення поступальних приводів за допомогою наведеного програмно-математичного апарату, що планується перевірити експериментально на діючому макеті верстата, який розробляється.
The structural analysis of form-building movements in machine tools with parallel kinematics is lead. The software -mathematical device for the kinematic analysis and management of position of parts of spatial mechanisms with bars of constant length is developed.
1. Бергер Э.Г., Табацков В.П. Синтез механизмов в машиностроении и робототехнике. – Николаев, НГАУ, 2004 ‑ 188с.
2. Агрегатно-модульне технологічне обладнання: у 3-х част. Під ред. Ю.М. Кузнєцова. Навч. посібник для ВНЗ. – Кіровоград, 2003 р.
3. Крижанівський В.А., Кузнєцов Ю.М., Валявський І.А., Скляров Р.А. Технологічне обладнання з паралельною кінематикою.‑ Кіровоград, 2004. ‑ 449с.
4. Кузнєцов Ю.М., Крижанівський В.А., Скляров Р.А. Сучасний стан, прогнозування і перспективи розвитку верстатів з паралельною кінематикою. Зб. наукових праць "Процеси механічної обробки в машинобудуванні", ЖДТУ, Вип. 1, 2005. – с.320 – 333.
5. Кузнєцов Ю.М. Світові тенденції і перспективи розвитку верстатобудування в Україні // Збірник наукових праць за матеріалами науково-методичної конференції "Проблеми фізико-математичної і технічної освіти і науки України в контексті євроінтеграції (Вища освіта‑2006)".‑ К.: НПУ ім. М.П. Драгоманова, 2007. – с.45 ‑55.
6. Обрабатывающее оборудование нового поколения. Концепция проектирования / В.Л. Афонин, А.Ф. Крайнев, В.Е. Ковальов и др.; Под ред. В.Л. Афонина. М.: Машиностроение, 2001. – 256 с.
7. Справочник по математике для инженеров и учащихся втузов. Бронштейн И.Н., Семендяев К.А. – М.:Наука, 1981. – 718 с.
8. Q. Huang, H. Hadeby, G. Sohlenius. Connection Method for Dynamic Modelling and Simulation of Parallel Kinematic Mechanism (PKM) Machines// Int J Adv Manuf Technol (2002) 19:163–173, 2002 Springer-Verlag London, Limited.
9. M. Honegger. Nonlinear adaptive control of a 6 DOF parallel manipulator / Institute of Robotics, ETH Zurich, Switzerland, honegger@ifr.mavt.ethz.ch
10. Simulation und Kalibration von Parallelkinematiken / IWF, ETH-Zentrum, Tannenstrasse 3, CH-8092 Zürich, http://www.iwf.mavt.ethz.ch
11. M. Valasek, Z. Sika, V. Bauma, T. Vampola Tractable Treatment of Design by Multiobjective Optimization – Parallel Kinematics Case Study // Multibody System Dynamics (2005) 13: р. 143–174, Springer 2005.
Ответы на вопросы [_Задать вопроос_]
Читайте также
Современные технические средства, комплексы и системы
Краснов В.А., Прохорович А.В., Шутов С.В., Деменский А.Н. Анализ флуктуаций размера растущего кристалла (на примере легированных монокристаллов кремния, вытягиваемых из расплава по методу Чохральского)Завальнюк И.П. Управление высокопроизводительной экструзией неоднородных материалов
Долина В.Г., Писаренко А.В. Синтез складної багатовимірної системи управління випарною станцією на основі рефрактометричних вимірювань
Стопакевич А.А., Тодорцев Ю.К. Анализ современного состояния систем управления брагоректификационными установками спиртового производства
Поливода В.В. Современные компьютерные технологии в АСУ на хлебоприёмном предприятии
Ладанюк А.П., Українець А.І., Кишенько В.Д. Управління автоматизованими технологічними комплексами харчових виробництв на основі сценарного підходу
Ковриго Ю.М., Фоменко Б.В. Врахування обмежень для підвищення якості функціонування систем регулювання енергоблоків ТЕС і АЕС
Евдокимов А.В., Китаев А.В., Агбомассу В.Л. Исследование причин, определяющих вращение рамки с током в магнитном поле после воздействия на нее внешнего импульса
Аппазов Э.С. Применение твердых растворов InGaN в фотовольтаике
Черевко О.И., Ефремов Ю.И., Одарченко А.М., Одарченко Д.М, Агафонова Ю.Ю. Теоретическое обоснование перспективного биконического резонатора для СВЧ-устройств при переработке растительного сырья
Хобин В.А. Бабиков А.Ю. Системы экстремального управления молотковыми дробилками с функцией гарантированного соблюдения тепловых режимов их электродвигателей.
Стадниченко В.Н. Исследование влияния изменения эксплуатационных нагрузок на свойства металлокерамических слоёв полученных с использованием трибовосстанавливающих составов
Ісаєв Е.А., Наговський Д.А., Чернецька І.Е. До вибору факторів, що характеризують окомкування тонкоподрібнених залізорудних матеріалів
Федоровский К.Ю., Лунев А.А. Теплоотдача погружного пластинчатого теплообменника системы охлаждения энергоустановок морских технических средств
Федоровский К.Ю., Владецкий Д.О. Интенсификация теплоотвода замкнутых систем охлаждения энергоустановок морских технических средств.
Пономарьов Я.Ю., Ладанюк А.П., Іващук В.В. Досвід використання нечітких регуляторів в системі атоматизації випарної установки.
Левченко А.А., Кравчук О.И. Эквивалентный макромодуль процесса технического обслуживания радиотехнических средств.
Іволгіна Т.О. Енергетичний підхід до аналізу стійкості руху вимірювальної головки координатно-вимірювальної машини
Ладанюк А.П., Кишенько В.Д., Ладанюк О.А. Системна задача управління біотехнологічними процесами.
Тернова Т.І. Алгоритм оцінювання деформацій рапорту періодичних об'єктів
Рожков С.А., Федотова О.Н. Алгоритм обучения системы распознавания автоматической системы разбраковки тканей
Пупена О.М, Ельперін І.В, Ладанюк А.П. Особливості проектування комп’ютерно-інтегрованих систем управління
Квасніков В.П., Кочеткова О.В. Проектування координатно–вимірювальної машини на нейронних мережах
Водічев В.А., Мухаммед М.А. Дослідження системи стабілізації потужності різання металообробного верстата з фази-регулятором
Шутов С.В., Аппазов Э.С., Марончук А.И., Самойлов Н.А. Методика испытания термофотовольтаических преобразователей
Хобин В.А. Повышение качества формирования смесей средствами интеллектуализации алгоритмов управления порционным дозированием
Терновая Т.И. Автоматическая система разбраковки тканей с печатным рисунком методом компенсации информационных потоков
Рожков С.А., Бражник Д.А. Использование нейросетевых структур для построения систем распознавания образов
Місюра М.Д., Кишенько В.Д. Математичні моделі технологічних процесів пивоварного виробництва як об’єктів автоматизації
Ладанюк А.П., Власенко Л.О. Автоматизоване управління бізнес-процесами в комп’ютерно-інтегрованих структурах підприємства
Жукова Н.В., Литвинов В.І. Вирішення проблеми погодженого руху валків з неоднаковими катаючими діаметрами профілезгинальних станів
Денисова А.Е., Тодорцев Ю.К., Максименко И.Н. К вопросу об автоматизации интегрированной установки теплоснабжения с возобновляемыми источниками энергии
Бессараб В.И. Компьютеризированная система управления водоотливным хозяйством угольных шахт по критерию минимума энергозатрат
Хобин В.А. Регулятор переменной структуры для объектов технологического типа
Тонконогий В.М. Трехконтурная АСУ нанесением ионно-плазменного покрытия на режущий инструмент.
Колесникова Е.В., Кострова Г.В. Формирование базы данных АСУТП дуговой сталеплавильной печи.
Водічев В.А. Автоматизована система керування швидкостями робочих рухів то-карного верстата для підвищення ефективності обробки торцевих поверхонь.
Бергер Е.Г., Дмитрієв Д.О., Бергер Є.Е., Діневич Г.Ю. Синтез строфоїдографів за методом параметричних сімей.
Бабак В.П., В.Н. Стадніченко, О.Г. Приймаков Прогнозування надійності, дов-говічності та витривалості авіаційних матеріалів
Бабак В.П., Стадниченко В.Н., Приймаков О.Г., Токарчук В.В. Прогнозування витривалості авіаційних матеріалів .
Куцак Р.С. Використання методу координатного еталону в задачах автоматизації контролю якості тканини.
Попруга А.Г. Усовершенствование электрических нагревателей по критерию экономии энергии.
Пашковский А.А., Далечин А.Ю. Система регистрации спектров фотолюминес-ценции
Никольский В.В., Цюпко Ю.М. Применение пьезоэлектрических датчиков в сис-теме кондиционирования воздуха судовых систем микроклимата.
Крапивко Г.И., Хлопёнова И.А. Повышение коэффициента полезного действия кремниевых фотоэлектронных преобразователей методом лазерной гравировки.
Кихтенко Д.А. Управление шаговыми двигателями в микрошаговом режиме, оп-тимизация управления.
Горохов В.А. Автоматизированная транспортно-складская система в текстильной и легкой промышленности.
Водічев В.А. Система стабілізації потужності різання фрезерного верстата з взаємозв'язаним керуванням швидкостями робочих рухів.
Шутов С.В., Аппазов Э.С., Марончук А.И. Испытание фотоэлектрических преобразователей в условиях экстремальных температурных колебаний.
Худяев А.А. К проблеме повышения точности воспроизведенияв классе многоканальных воспроизводящих систем с эталонной настройкой каналов.
Тверезовський В.С., Бараненко Р.В. Принцип побудови елементів вимірювальних систем, представлених цифровими програмно керованими давачами.
Никольский В.В., Сандлер А.К. Моделирование процессов в вискозиметре с пьезоэлектрическим приводом.
Марончук И.Е., Андронова Е.В., Баганов Е.А., Курак В.В. Использование метода импульсного охлаждения насыщенного раствора-расплава для формирования наноразмерных структур InSb в матрице GaSb.
Водічев В.А. Аналого-цифровий регулятор режиму металообробки для верстатів з числовим програмним керуванням.
Блинов Э.И., Кравцов В.И., Кравцов А.В., Недбайло А.Н. Управление гибкими протяженными объектами направленными силовыми воздействиями.