УДК 648.058.602.23
ТЕОРЕТИЧЕСКОЕ ОБОСНОВАНИЕ ПЕРСПЕКТИВНОГО БИКОНИЧЕСКОГО РЕЗОНАТОРА ДЛЯ СВЧ-УСТРОЙСТВ ПРИ ПЕРЕРАБОТКЕ РАСТИТЕЛЬНОГО СЫРЬЯ
Черевко О.И., Ефремов Ю.И., Одарченко А.М., Одарченко Д.М, Агафонова Ю.Ю.
В Украине наметилась положительная тенденция использования СВЧ-энергии при переработке растительного сырья. Это обусловлено, прежде всего, преимуществами этого подвода энергии, которая позволяет сократить продолжительность технологической обработки, что приводит к снижению расходов топливно-энергетических ресурсов, отсутствия образования канцерогенных веществ, благоприятные санитарно-гигиенические условия работы для персонала и снижению потерь массы при обработке за счет равномерного распределения температурного поля. В этой связи теоретическое обоснование основных характеристик основного конструктивного элемента СВЧ-устройств резонаторов стоит особо остро. Поэтому основной целью статьи является проведение расчета полей в биконическом резонаторе и проведения контроля над диэлектрическими характеристиками растительного сырья, что повысит добротность резонаторов, что, соответственно, резко повысит технологичность в проведении процесса.
Приводим решение предложенной выше математической модели для биконического резонатора, то есть резонатора, центральная часть которого является цилиндром, а торцы – усеченными конусами (рис. 1).
Область II описывается цилиндрическими координатами, поэтому в этой части резонатора можно представить в виде:
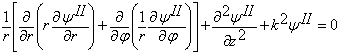 (1)
(1)
где ψII – продольная электрическая (поперечная магнитная) или продольная магнитная (поперечная электрическая) скалярная функция в центральной части II.
Уравнение 1 решается с помощью метода разделения переменных. Предположим, что
ψII = P(r).Ф(φ).Z(z), (2)
где r, φ, z – текущие координаты цилиндрической системы.
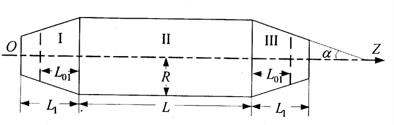
Рис. 1 Схематическое изображение биконического резонатора
Подставим (2) в (1):
![]() (3)
(3)
Разделив выражение (3) на (2) получаем три независимых уравнения для каждой из неизвестных функций P(r), Ф(φ) и Z(z):
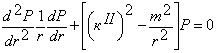 , (4)
, (4)
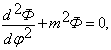 (5)
(5)
![]() (6)
(6)
Как известно, решением дифференциального уравнения (4) являются функции Бесселя первого Jm(кIIr) и второго Nm(кIIr) рода
P(r) = A1. Jm(кIIr)+A2. Nm(кIIr), (7)
где т - число, определяющее порядок данных функций.
Поскольку решение на оси резонатора должно быть конечным, необходимо, учитывая поведение функции Бесселя второго рода при стремящемся к нулю ее аргументе, коэффициент A2 положить равным нулю. Тогда
P(r) = A1. Jm(кIIr), (8)
где кII – волновое число.
Дифференциальное уравнение (5) имеет решением функцию
Ф = А3.cos(m.φ) + A4.sin(m.φ), (9)
где т - тоже число, что и в (8).
Выбирая соответствующим образом начало отсчета координаты φ, можно получить А4=0. Таким образом,
Ф = А3.cos(m.φ). (10)
Учитывая, кроме того, что при изменении угла φ на 2π радиан должно быть получено то же самое распределение электромагнитного поля, можно сделать вывод, что т - целое число.
Из уравнения (6) следует, что
Z = ![]() (11)
(11)
где βII – продольное волновое число в области II резонатора.
Появление в показателе степени разности (z – L1) связано с тем, что начало отсчета по оси OZ в области II находится в точке L1. Первое слагаемое в выражении (11) характеризует волну, распространяющуюся в положительном направлении оси OZ, второе – в отрицательном.
Подставляя полученные выражения (8), (10) и (11) в (12), получаем продольную скалярную функцию в области II резонатора в цилиндрической системе координат:
ψII = Jm(к r) cos (mφ)[ ![]() ], (12)
], (12)
где А'1 = А1 – А3 – А5, А'2 = А1– А3 – А6.
Для вычисления собственных значений оператора или, что то же самое, поперечных волновых чисел, воспользуемся граничными условиями на контуре поперечного сечения, то есть при выполнении равенства r = R.. Для колебаний типа ТМ (продольные электрические волны) следует:
Jm(![]() R) = 0, (13)
R) = 0, (13)
откуда поперечное волновое число кTM для волн типа ТМ определяется выражением
![]() =
= ![]() (14)
(14)
где μтп – n-ый корень функции Бесселя Jm(![]() r).
r).
Таким образом, продольное волновое число в этом случае определяется выражением:
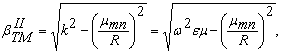 (15)
(15)
где ω = 2πf – круговая частота возбуждающего резонатор электромагнитного поля;
ε и μ – абсолютная диэлектрическая и магнитная проницаемость заполнения волновода, соответственно.
Основываясь на граничном условии, получаем из (2) для r = R:
![]() |r = R = 0, (16)
|r = R = 0, (16)
откуда следует, что поперечное волновое число ктеII для волн типа ТЕ будет равно:
![]() =
= ![]() (17)
(17)
где μтп’ – n-ый корень производной функции Бесселя первого рода.
Для этого случая продольное волновое число βTEII определяется из выражения:
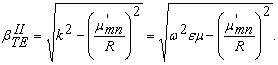 (18)
(18)
Используя 'полученные в (14), (15), (17), (18) выражения для поперечных и продольных волновых чисел в случае ТМ и ТЕ волн получаем окончательные выражения для соответствующих собственных скалярных функций в области II резонатора:
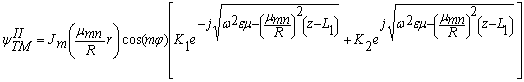 (19)
(19)
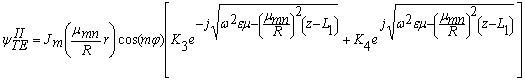 (20)
(20)
где К1, К2 – неизвестные коэффициенты, которые соответствуют коэффициентам А'1, А'2 из выражения (12) в случае ТМ-волн, а К3, К4 – в случае ТЕ-волн.
Полученные для области II резонатора решения позволяют перейти теперь к рассмотрению областей I и III, используя тот же метод разделения переменных, что и выше. Будем искать собственную скалярную функцию ψ в виде, аналогичном (12):
ψI,II = P(r).Ф(φ).Z(z). (21)
Исходя из плавного перехода области II резонатора в область I, а также монотонного изменения поперечного сечения области I можно считать, что в левой части резонатора решения уравнений (4) и (5) будут иметь тот же вид (8) и (10), что и в области II. Но поскольку здесь радиус поперечного сечения является функцией z, то есть
R1(z) = R – (L1 - z)tgα, (22)
то и
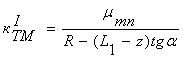 , (23)
, (23)
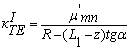 . (24)
. (24)
Это приводит к тому, что продольные волновые числа ![]() и
и ![]() будут также функцией продольной координаты z:
будут также функцией продольной координаты z:
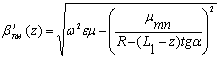 , (25)
, (25)
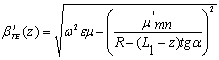 . (26)
. (26)
Для решения уравнения (6) в области I необходимо воспользоваться методом присоединенных функций. Тогда функция Z(z) в случае волны типа ТМ будет иметь вид
Z(z) = К5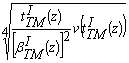 , (27)
, (27)
а для волны типа ТЕ –
Z(z) = К6 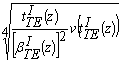 , (28)
, (28)
где К5, К6 – неизвестные коэффициенты.
На основании полученных результатов скалярную функцию ψI для случаев ТМ и ТЕ-волн, используя выражение (21), можно представить в виде:
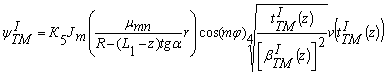 , (29)
, (29)
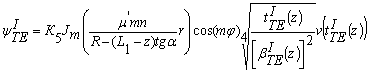 , (30)
, (30)
где
![]() = -
= -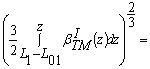
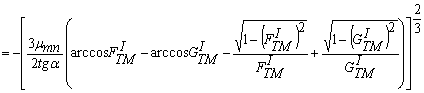 ; (31)
; (31)
![]() = -
= -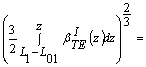
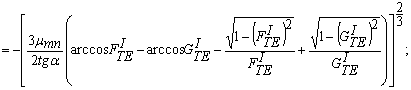 (32)
(32)
![]() =
= ![]() ;
;
![]() =
= ![]() ;
;
![]() =
= 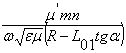 ;
;
![]() =
= 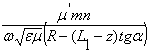 ;
;
В области III резонатора функция ψIII находится из выражений, аналогичных (29), (30), но в этом случае радиус определяется соотношением:
RIII (z) = R – (z – L – L1) tgα (33)
Таким образом,
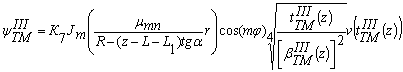 , (34)
, (34)
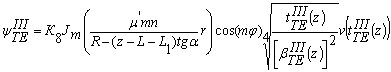 , (35)
, (35)
где
![]() = -
= -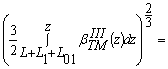
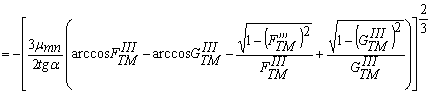 ; (36)
; (36)
![]() = -
= -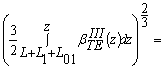
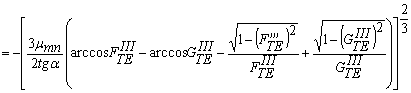 ; (37)
; (37)
![]() =
=![]() ;
;
![]() =
=![]() ;
;
![]()
![]() ;
;
![]()
![]() ;
;
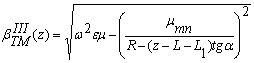 ;
;
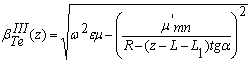 .
.
Полученные выражения (19), (20), (24), (25), (34), (35) описывают распределение электромагнитного поля во всех трех областях резонатора для случаев ТМ и ТЕ-волн.
Таким образом, теоретическое описание и расчет основных параметров биконического резонатора СВЧ-устройств позволяют констатировать необходимости применения биконического резонатора для непрерывной технологической обработки растительного сырья.
In article the theoretical description and calculation of key parameters the biconical resonator for continuous technological processing vegetative raw material is considered
1. Тихонов А.И., Самарский А.А. Уравнения математической физики. – М.: Наука, 1986. – 724 с.
2. Ильин В.А., Позняк Э.Г. Линейная алгебра. – М.: Наука, 1978. – 302 с.
3. Григорьев А.Д., Янкевич В.Б. Резонаторы и резонаторные замедляющиеся системы СВЧ: системные методы расчета и проектирования. – М.: Редко и связь. 1984. – 248 с.
Ответы на вопросы [_Задать вопроос_]
Читайте также
Современные технические средства, комплексы и системы
Краснов В.А., Прохорович А.В., Шутов С.В., Деменский А.Н. Анализ флуктуаций размера растущего кристалла (на примере легированных монокристаллов кремния, вытягиваемых из расплава по методу Чохральского)Завальнюк И.П. Управление высокопроизводительной экструзией неоднородных материалов
Долина В.Г., Писаренко А.В. Синтез складної багатовимірної системи управління випарною станцією на основі рефрактометричних вимірювань
Стопакевич А.А., Тодорцев Ю.К. Анализ современного состояния систем управления брагоректификационными установками спиртового производства
Поливода В.В. Современные компьютерные технологии в АСУ на хлебоприёмном предприятии
Ладанюк А.П., Українець А.І., Кишенько В.Д. Управління автоматизованими технологічними комплексами харчових виробництв на основі сценарного підходу
Ковриго Ю.М., Фоменко Б.В. Врахування обмежень для підвищення якості функціонування систем регулювання енергоблоків ТЕС і АЕС
Евдокимов А.В., Китаев А.В., Агбомассу В.Л. Исследование причин, определяющих вращение рамки с током в магнитном поле после воздействия на нее внешнего импульса
Аппазов Э.С. Применение твердых растворов InGaN в фотовольтаике
Кузнєцов Ю.М., Дмитрієв Д.О. Програмно математичний апарат керування виконавчим органом багатокоординатних верстатів нових компоновок
Хобин В.А. Бабиков А.Ю. Системы экстремального управления молотковыми дробилками с функцией гарантированного соблюдения тепловых режимов их электродвигателей.
Стадниченко В.Н. Исследование влияния изменения эксплуатационных нагрузок на свойства металлокерамических слоёв полученных с использованием трибовосстанавливающих составов
Ісаєв Е.А., Наговський Д.А., Чернецька І.Е. До вибору факторів, що характеризують окомкування тонкоподрібнених залізорудних матеріалів
Федоровский К.Ю., Лунев А.А. Теплоотдача погружного пластинчатого теплообменника системы охлаждения энергоустановок морских технических средств
Федоровский К.Ю., Владецкий Д.О. Интенсификация теплоотвода замкнутых систем охлаждения энергоустановок морских технических средств.
Пономарьов Я.Ю., Ладанюк А.П., Іващук В.В. Досвід використання нечітких регуляторів в системі атоматизації випарної установки.
Левченко А.А., Кравчук О.И. Эквивалентный макромодуль процесса технического обслуживания радиотехнических средств.
Іволгіна Т.О. Енергетичний підхід до аналізу стійкості руху вимірювальної головки координатно-вимірювальної машини
Ладанюк А.П., Кишенько В.Д., Ладанюк О.А. Системна задача управління біотехнологічними процесами.
Тернова Т.І. Алгоритм оцінювання деформацій рапорту періодичних об'єктів
Рожков С.А., Федотова О.Н. Алгоритм обучения системы распознавания автоматической системы разбраковки тканей
Пупена О.М, Ельперін І.В, Ладанюк А.П. Особливості проектування комп’ютерно-інтегрованих систем управління
Квасніков В.П., Кочеткова О.В. Проектування координатно–вимірювальної машини на нейронних мережах
Водічев В.А., Мухаммед М.А. Дослідження системи стабілізації потужності різання металообробного верстата з фази-регулятором
Шутов С.В., Аппазов Э.С., Марончук А.И., Самойлов Н.А. Методика испытания термофотовольтаических преобразователей
Хобин В.А. Повышение качества формирования смесей средствами интеллектуализации алгоритмов управления порционным дозированием
Терновая Т.И. Автоматическая система разбраковки тканей с печатным рисунком методом компенсации информационных потоков
Рожков С.А., Бражник Д.А. Использование нейросетевых структур для построения систем распознавания образов
Місюра М.Д., Кишенько В.Д. Математичні моделі технологічних процесів пивоварного виробництва як об’єктів автоматизації
Ладанюк А.П., Власенко Л.О. Автоматизоване управління бізнес-процесами в комп’ютерно-інтегрованих структурах підприємства
Жукова Н.В., Литвинов В.І. Вирішення проблеми погодженого руху валків з неоднаковими катаючими діаметрами профілезгинальних станів
Денисова А.Е., Тодорцев Ю.К., Максименко И.Н. К вопросу об автоматизации интегрированной установки теплоснабжения с возобновляемыми источниками энергии
Бессараб В.И. Компьютеризированная система управления водоотливным хозяйством угольных шахт по критерию минимума энергозатрат
Хобин В.А. Регулятор переменной структуры для объектов технологического типа
Тонконогий В.М. Трехконтурная АСУ нанесением ионно-плазменного покрытия на режущий инструмент.
Колесникова Е.В., Кострова Г.В. Формирование базы данных АСУТП дуговой сталеплавильной печи.
Водічев В.А. Автоматизована система керування швидкостями робочих рухів то-карного верстата для підвищення ефективності обробки торцевих поверхонь.
Бергер Е.Г., Дмитрієв Д.О., Бергер Є.Е., Діневич Г.Ю. Синтез строфоїдографів за методом параметричних сімей.
Бабак В.П., В.Н. Стадніченко, О.Г. Приймаков Прогнозування надійності, дов-говічності та витривалості авіаційних матеріалів
Бабак В.П., Стадниченко В.Н., Приймаков О.Г., Токарчук В.В. Прогнозування витривалості авіаційних матеріалів .
Куцак Р.С. Використання методу координатного еталону в задачах автоматизації контролю якості тканини.
Попруга А.Г. Усовершенствование электрических нагревателей по критерию экономии энергии.
Пашковский А.А., Далечин А.Ю. Система регистрации спектров фотолюминес-ценции
Никольский В.В., Цюпко Ю.М. Применение пьезоэлектрических датчиков в сис-теме кондиционирования воздуха судовых систем микроклимата.
Крапивко Г.И., Хлопёнова И.А. Повышение коэффициента полезного действия кремниевых фотоэлектронных преобразователей методом лазерной гравировки.
Кихтенко Д.А. Управление шаговыми двигателями в микрошаговом режиме, оп-тимизация управления.
Горохов В.А. Автоматизированная транспортно-складская система в текстильной и легкой промышленности.
Водічев В.А. Система стабілізації потужності різання фрезерного верстата з взаємозв'язаним керуванням швидкостями робочих рухів.
Шутов С.В., Аппазов Э.С., Марончук А.И. Испытание фотоэлектрических преобразователей в условиях экстремальных температурных колебаний.
Худяев А.А. К проблеме повышения точности воспроизведенияв классе многоканальных воспроизводящих систем с эталонной настройкой каналов.
Тверезовський В.С., Бараненко Р.В. Принцип побудови елементів вимірювальних систем, представлених цифровими програмно керованими давачами.
Никольский В.В., Сандлер А.К. Моделирование процессов в вискозиметре с пьезоэлектрическим приводом.
Марончук И.Е., Андронова Е.В., Баганов Е.А., Курак В.В. Использование метода импульсного охлаждения насыщенного раствора-расплава для формирования наноразмерных структур InSb в матрице GaSb.
Водічев В.А. Аналого-цифровий регулятор режиму металообробки для верстатів з числовим програмним керуванням.
Блинов Э.И., Кравцов В.И., Кравцов А.В., Недбайло А.Н. Управление гибкими протяженными объектами направленными силовыми воздействиями.