Автоматика.
    Автоматизация.
        Электротехнические
            комплексы и системы.

УДК 681.51

АЛГОРИТМ ОБУЧЕНИЯ СУБОПТИМАЛЬНОМУ ПО БЫСТРОДЕЙСТВИЮ УПРАВЛЕНИЮ ДИНАМИЧЕСКОЙ СИСТЕМОЙ ВТОРОГО ПОРЯДКА БЕЗ НУЛЕВЫХ ПОЛЮСОВ

Кучеров Д.П.

Введение. При построении целого ряда технических задач управления часто возникает необходимость перевода объекта из одного состояния в другое за минимальное время. Хотя решение этой задачи, которая получила известность как задача построения системы, оптимальной по быстродействию, в простейшем случае было найдено еще в 50-х годах прошлого века [1], она до сих пор продолжает привлекать внимание исследователей [2].

Постановка упомянутой задачи прежде включала предположение, что все параметры объекта априори известны конструктору системы. В действительности же в реальных условиях такая информация может отсутствовать. В этом случае представляется целесообразным использование адаптивного подхода, позволяющего восполнить недостающую априорную информацию путем надлежащей обработки сигналов, которые циркулируют в замкнутой системе [3]. В рамках этого подхода на основе идей обучения распознавания образов в [4] был предложен метод обучения регулятора, обеспечивающего субоптимальное по быстродействию управление объектом второго порядка с двумя нулевыми полюсами при отсутствии помех измерения. Позже в [5-7] этот подход был распространен на случай, когда в каналах измерений имеются помехи.

Особенностью задач, рассмотренных в [5-7], является то, что характеристическая функция регулятора зависит линейно от неизвестных параметров объекта. Сравнительно недавно удалось получить решение такой задачи для объекта второго порядка с одним нулевым полюсом, которое сводится к построению характеристической функции, нелинейно зависящей от одного неизвестного параметра [8].

Известно решение задачи оптимального по быстродействию управления объектом второго порядка без нулевых полюсов [9]. Для решения этой задачи в субоптимальной постановке при неполной априорной информации о параметрах объекта в принципе можно было бы использовать тот же подход, что и работе [8]. Однако построенный на основе упомянутого подхода алгоритм обучения будет обладать низкой скоростью сходимости, поскольку в отличие от [8] характеристическая функция регулятора согласно [9] зависит нелинейно не от одного, а от двух неизвестных параметров.

Ниже предлагается алгоритм обучения субоптимальному по быстродействию управлению объектом второго порядка без нулевых полюсов, основанный на использовании идеи нелинейной классификации, заимствованной из работы [10].

Постановка задачи. Пусть имеется объект, который представляет собой последовательное соединение двух инерционных звеньев с постоянными времени Т₁, Т₂ и описывается передаточной функцией

,                                                           (1)

имеющей два ненулевых полюса в точках s₁=1/T₁, s₂=1/T₂.

Нетрудно показать [1, 9], что передаточной функции (1) соответствует система дифференциальных уравнений

,  ,                          (2)

.                                                           (3)

В этих уравнениях k₁=-T₁/(T₂-T₁), k₂=T₂/(T₂-T₁), u(t) - управляющее воздействие, принимающее одно из двух значений ±1, x(t) - выходная величина, а x₁(t), x₂(t) - новые фазовые переменные. Как и в [4], предполагается, что переменные x₁(t) и x₂(t) доступны для измерения, а помехи в измерительных каналах отсутствуют.

Предполагается, что априорная информация о постоянных времени T₁, T₂ и коэффициенте усиления k объекта отсутствует.

Задача состоит в том, чтобы в условиях априорной неопределенности относительно значений T₁, T₂ и k, выраженной в форме

,                                    (4)

построить алгоритм управления, обеспечивающий перемещение вектора z(n, t) = [x₁(n, t), x₂(n, t)]^T из любого начального состояния z(n, 0)̲ в некоторую достаточно малую наперед заданную окрестность W̲ начала координат (область достижимости) за минимально возможное время с изменением знака управления не более одного раза для всех достаточно больших n, где n=1, 2, …- порядковый номер цикла ²испытаний². При этом размеры области W должны быть ²по возможности² малыми.

Алгоритм обучения управлению. Согласно [1, 9] оптимальное по быстродействию управление объектом в форме (2), (3) при наличии полной априорной информации о параметрах k, T₁, T₂ определяется как

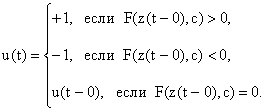                                               (5)

Здесь

                                   (6)

- линия переключения, положение которой в ² зависит от вектора параметров c^T=[c⁽¹⁾, c⁽²⁾, c⁽³⁾] с компонентами

c⁽¹⁾ = k,             c⁽²⁾ = k^-1,          c⁽³⁾ = T₂/T₁.                                        (7)

Поскольку по условию задачи параметры k, T₁, T₂ априори неизвестны, то реализация закона управления (5) в силу (6), (7) не представляется возможным. В этом случае, как в [4-8], перейдем от управления (5) к управлению

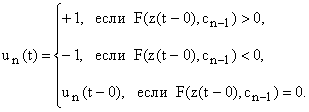                                               (8)

в котором

                            (9)

имеет смысл текущей характеристической функции регулятора, зависящей от z^T = [x₁, x₂] и вектора

.                                                  (10)

Скалярная функция (9) получается заменой в выражении для оптимальной функции переключения (6) вектора неизвестных параметров c^T = [c⁽⁰⁾, c⁽¹⁾, c⁽²⁾, c⁽³⁾], в котором c⁽⁰⁾=l, c⁽¹⁾=lk, c⁽²⁾=k^-1, c⁽³⁾=T₂/T₁, на соответствующие оценки , выстроенные на предыдущем n-м цикле с помощью некоторого алгоритма обучения. (Здесь l>0 – произвольное число.)

Как видно из выражения (9), компоненты c⁽²⁾, c⁽³⁾ входят в F(z, c) нелинейно и это существенный момент.

В соответствии с подходом, развиваемым в [4-8], реализация алгоритма обучения предусматривает запоминание координаты точки z(n, t_n), представляющей собой точку пересечения траектории движения z(n, t) с разделяющей линией

в некоторый момент t=t_n, когда она в первый раз пересечет ее и последующего анализа результата завершения n-го цикла испытаний. В качестве алгоритма обучения предлагается такая рекуррентная процедура:

(11)

В этом алгоритме m>0 – настроечный параметр, который согласно рекомендациям, данным в работе [10], желательно выбирать по возможности малым; Pr_X{c¢} - проектор произвольного вектора c¢ÎÂ⁴ на выпуклое множество X=[1, +¥)´[0, +¥)´[0, +¥)´[0, +¥)ÌÂ⁴,

;                                                         (12)

 (13)

D>0, e>0 – некоторые наперед заданные достаточно малые числа, выбираемые конструктором.

Алгоритм (8) совместно с (11)-(13) представляет собой модификацию алгоритма обучения нелинейной классификации образов, предложенного в [10]; при этом соотношение (13) представляет собой не что иное как реализация указаний ²учителя². В отличие от алгоритма работы [10], согласно которому вектор c_n должен корректироваться всякий раз независимо от результата распознавания вектора z(t_n), коррекция c_n по алгоритму (11) осуществляется только при наличии ошибки распознавания.

Выражения (8), (9) с учетом (11)-(13) определяют алгоритм адаптивного управления объектом (2), (3) полностью (после задания начальных условий, определяемых вектором c₀ Î X).

При построении алгоритма обучения (8), (11)-(13) использовано следующее положение.

Лемма. Для произвольной области достижимости W существует неодноточечное множество векторов параметров С Ì Â⁴, включающее вектор с, такое, что при любом с*ÎС закон управления

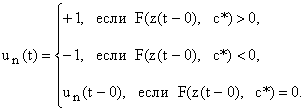
обеспечивает попадание вектора с_n(t) в область W с переключением u_n(t) не более одного раза на n-м цикле при произвольном ненулевом начальном векторе z_n(0).

Модельный эксперимент. Для демонстрации свойств сходимости алгоритма адаптации (11)-(13) и возможностей достижения цели управления проводилось машинное моделирование системы со следующими значениями параметров объекта (1): k = 1, T₁=0,2 с, T₂=0,8 c, для которого оптимальное время переходного процесса известно и равно t_opt=0,84 с. Величины e, m и D взяты равными e = 0,01, m = 0,01, D = 0,059. Область достижимости W определялась как W = {z: |x₁| £ 0,016, |x₂| £ 0,057}. Проводились эксперименты при различных начальных векторах состояний z(n, 0) и начальных векторах параметров c₀.

Результаты моделирования для случая, когда , а  приведены на рис.1-4. На рисунках представлена динамика переменных x(t), y(t)=dx(t)/dt и u(t). Оказалось, что на первом цикле испытаний после пересечения траекторией движения точки z(t) линии переключения F(z, c₀)=0 система переходит в скользящий режим в момент t = 0,59 c (см. рис.1). На рис. 2 показано изменение тех же переменных, что и на рис.1 после завершения процесса обучения. Как видно из рис.2, теперь уже точка z(t) переходит из начального состояния z(0) в область W с одним переключением u(t) за время t=0,84 c, т.е. цель управления достигается.

Моделирование процесса обучения показало, что в условиях эксперимента продолжительность этого процесса составила n_max = 18 циклов; при этом изменение вектора c_n полностью прекращалось при всех n ³ n_max + 1.

В данном эксперименте последовательность {c_n} сходилась к вектору c* = (1,814, 3,858, 0,445, 4,866)^T, отличающемуся от c (как и следовало ожидать). Изменение составляющих вектора c_n при nÎ[0, 18] графически изображено на рис. 3.

Для того чтобы оценить, сходится ли последовательность {c_n} в некоторую окрестность C точки c, проводилось вычисление значений функции

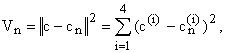
обычно используемой при анализе сходимости процессов адаптации. Эта функция представлена на рис.4.

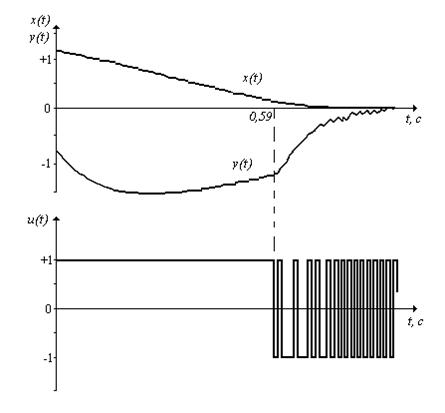
Рис.1 Переменные x(t), y(t) и u(t) на первом цикле обучения

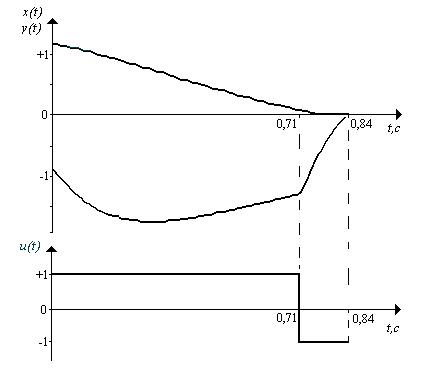
Рис.2 Переменные x(t), y(t) и u(t) на n_max ом цикле обучения

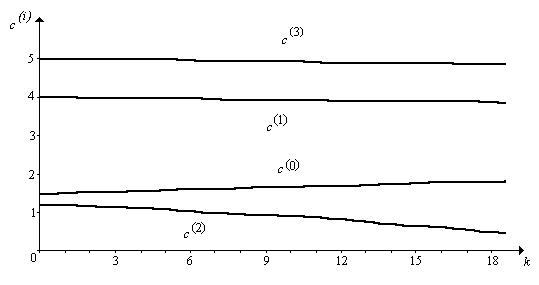
Рис.3 Компоненты вектора с⁽ⁱ⁾

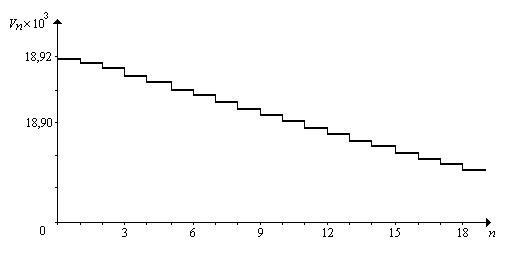
Рис. 4 Функция V_n

Оказалось, что V_n – убывающая функция при 0 £ n £ 18. Именно это свойство и обеспечило в данном случае сходимость {c_n} в область C.

Замечания. Как видно из (11), предлагаемый алгоритм адаптации параметров регулятора (11)-(13) принадлежит к классу алгоритмов с коррекцией ошибки. Однако в отличие от известных алгоритмов этого класса его реализация в общем случае совершенно не гарантирует еще, что первая разность функции V_n будет монотонно невозрастающей, т.е. что

V_n-V_{n -1} £ 0                                                                      (14)

для всех n = 1, 2, … Между тем условие (14) является достаточным для того, чтобы последовательность векторов {c_n} попадала в область C, если только в момент коррекции вектора c_n-1 изменение V_n строго отделено от нуля:

V_n-V_n-1 £ d < 0.                                                    (15)

В тоже время можно показать, что для выполнения (15) требуется, чтобы функция F(z, c¢) обладала свойством

при любом c¢ Î Â⁴ независимо от z [11, стр. 65]. А F(z, c), к сожалению, свойством (15) не обладает. Тем не менее, модельный эксперимент показывает, что {c_n} как в [10], все же стягивается в область C.

Выводы. Алгоритм адаптивного управления (8), (11)-(13) в принципе позволяет обеспечить субоптимальный по быстродействию переходный процесс в системе с объектом (2), (3) после завершения процесса обучения регулятора.

1.                  Смольников Л.П. Синтез квазиоптимальных систем автоматического управления. – Л.: Энергия, 1967. – 168 с.

2.                  Хабаров Н.В. Алгоритм решения задачи быстродействия на основе проектирования конечного состояния на множество достижимости // Труды ХХIV конференции молодых ученых механико-математического факультета МГУ им. М.В. Ломоносова (Москва, 8-13 апреля, 2002 г.). – С. 182-184.

3.                  Цыпкин Я.З. Основы теории обучающихся систем. – М.: Наука, 1970. – 252 с.

4.                  Кучеров Д.П. Об одной задаче синтеза адаптивной системы управления, субоптимальной по быстродействию// Праці П’ятої Української конференції з автоматичного управління “Автоматика-98”: Київ, 13-16 травня 1998 р. – ч.І. – К.: НТУУ “КПI”, 1998. – С.238-244.

5.                  Кучеров Д.П. Решение одной задачи синтеза адаптивной системы управления, квазиоптимальной по быстродействию, при наличии ограниченного шума // Кибернетика и вычисл. техника. – 1999. – Вып. 122. – С. 13 – 22.

6.                  Кучеров Д.П. Адаптивное квазиоптимальное по быстродействию управление некоторой динамической системой: идентификационный подход // Тр. Одес. политехн. ун-та. – Одесса, 2001. - Вып. 4 (16). - С. 78-81.

7.                  Кучеров Д.П. Об одном алгоритме обучения управлению, квазиоптимальному по быстродействию // Автоматика. Автоматизация. Электротехнические комплексы и системы. – Херсон, 2002. № 1 (10). – С.30-34.

8.                  Кучеров Д.П. Об адаптивном управлении инерционной системой второго порядка, субоптимальной по быстродействию // Наук. пр. ДонНТУ. Вип. 48. – Донецьк, 2002. – С. 63-69.

9.                  Атанс М., Фалб П. Оптимальное управление. – М.: Машиностроение, 1968. – 764 с.

10.              Blackmore K.L., Williamson R.C., Mareels I.M.Y. Learning nonlinearly parameterized decision regions // Journal of mathematical systems, estimation and control. - Vol. 6. – Number 1. – 1996. – P. 129-132.

11.              Фомин В.Н., Фрадков А.Л., Якубович В.А. Адаптивное управление динамическим объектами. – М.: Наука, - 1981.