УДК 66-9: 66-011
МАТЕМАТИЧНЕ МОДЕЛЮВАННЯ ПРОЦЕСУ ВІБРОКИПІННЯ СИПКИХ СЕРЕДОВИЩ
Русанов С., Луняка К., Карманов В.
Технологічні процеси, такі як сушіння сипких матеріалів, відновлення металів, обпалення гранул та інші, відбуваються в результаті взаємодії твердих частинок з газами або поверхнями. Вказані процеси як об’єкти управління є нестаціонарними, підданими координатним та параметричним збуренням, при цьому найчастіше найбільш ефективні режими роботи лежать в області гранично припустимих. Тому проблема забезпечення високої якості вихідних параметрів при зниженні енергоємності процесу є досить складним питанням. Це вимагає удосконалення існуючих математичних моделей та складання алгоритмів прогнозування [1].
Відомо також, що для цих процесів кращим шляхом інтенсифікації є створення умов активного перемішування, розпушення шару сипкого матеріалу і зниження опору на границі поділу фаз [2]. Тому широке застосування мають апарати з псевдозрідженим або віброкиплячим шаром. Та якщо для апаратів з псевдозрідженим шаром існують достатньо розроблені математичні моделі та параметри їх роботи добре регламентовані, то в теорії віброкипіння є багато недоробок. Для процесів з віброкиплячим шаром завдяки введенню вібрації кількість вхідних параметрів збільшується, водночас з цим відклик системи на зовнішні збурення дуже погано прогнозується і може вивести систему за межі гранично припустимих режимів роботи. Тому необхідна розробка моделі, що буде мати можливість врахувати максимально широкий діапазон чинників, що впливають на процес, але у той самий час адекватно враховувати характерні особливості віброкипіння, що може суттєво знизити її складність.
Відомо, що при впливі вібрації в сипучих тілах відбуваються перетворення, особливості яких обумовлюються інтенсивністю вібрації [2-4]. У міру збільшення інтенсивності вібрації, у межах амплітудних значень прискорень, не перевищуючі прискорення вільного падіння, сипуче тіло здобуває рухливість. Такий стан сипучого тіла прийнято називати станом віброзрідження. У цьому стані зчеплення між частками слабшає, зменшується число пор, досягається більш щільне укладання часток. Найбільше ущільнення досягається при амплітудних прискореннях коливань, близьких до прискорень вільного падіння. У цьому стані відсутні умови активного перемішування та він не є сприятливим для вищевказаних процесів.
При подальшому збільшенні інтенсивності коливань частки сипучого тіла починають втрачати контакт із вібруючим робочим органом, зменшуються й періодично порушуються зв'язки між частками; сипуче тіло переходить як би в стан кипіння. Цей стан, який має назву віброкипіння, характеризується розпушенням сипучого тіла й посиленою циркуляцією його частинок, що й обумовило його використання.
Перехід від віброзрідження до віброкипіння відбувається або при наданні сипучому тілу прискорень коливань певного рівня, або при досягненні певного енергетичного рівня. Перший критерій більш підходить до грубодисперсних систем, другий - до мікрогетерогенних. Перехід від стану віброзрідження до віброкипіння здійснюється, як правило, при прискореннях, що перевищують прискорення вільного падіння. Критичні прискорення й енерговитрати залежать від властивостей сипучого тіла, товщини шару, сил зчеплення між частками й інших факторів. Для промислових вібраційних систем перехід шару з одного стану в інший спостерігається у деяких випадках лише при інтенсивності вібрації, яка перевищує 10g.
Під впливом вібрації в тілах поширюються хвилі деформації. Моношар, що входить у контакт з джерелом вібрації, одержує від нього силові імпульси. Від нижнього моношару імпульси передаються лежачим вище моношарам. Внаслідок інерційності, наявності сил тертя й незворотних деформацій імпульси, в міру передачі їх від моношару до моношару, поступово слабшають, причому ступінь їхнього ослаблення визначається властивостями середовища, а також характером і величиною силових імпульсів. Енергія коливального руху джерела вібрації в процесі проходження хвилі витрачається на прискорення оброблюваного середовища й заповнення втрат при незворотних деформаціях.
Процес віброобробки сипучих тіл у значній мірі формується під впливом газової або рідкої фази. Внаслідок поганої повітропроникності сипуче тіло піддається великим аеродинамічним навантаженням. Аеродинамічні опори виникають у результаті того, що між пульсаціями тиску газової фази й рухом твердої фази є зрушення фаз. Внаслідок цього виникають аеродинамічні сили, що перешкоджають руху твердої фази. Так, у просторі між поверхнею робочого органу й нижнім моношаром сипучого тіла при підкиданні виникає розрідження, а при падінні - підвищення тиску щодо атмосферного. Зрівняння цих періодичних коливань тиску досягається внаслідок періодичного відтоку надлишкової й припливу відсутньої кількості повітря, що проходить через пори, наявні в шарі сипучого тіла. Аеродинамічні сили, що діють на частки, є головним чином функцією маси вантажу, питомої газопроникності й залежать від режиму коливань.
В багатьох роботах [2,4-6] для описання руху газу крізь віброкиплячий шар приймалася модель фільтрації газу в пористому середовищі. Така модель відрізняється простотою, однак має низку недоліків, пов’язаних з нехтуванням впливу на віброкиплячий шар таких важливих чинників, як змінна по висоті порізність шару і взаємодія частинок між собою і зі стінками апарату, тому такий підхід можна вважати достатньо грубим наближенням. Однак у деяких випадках така модель все ж дає прийнятні результати.
У загальному випадку віброкиплячий шар можна представити як двофазну систему (газ – тверді частинки). Як відомо, математичне описання двофазних середовищ базується на системі диференціальних рівнянь нерозривності, руху та енергії для кожної фази. [4, 7-10]. Нехтуючи змінами температури, рівняння енергії опускають і систему записують у вигляді [7-9]:
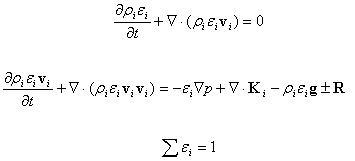 (1)
(1)
де ri – густина i-ї компоненти, i=s,g;
ei –об’ємна концентрація i-ї компоненти (eg - порізність);
vi – вектор швидкості i-ї компоненти;
p – тиск;
Кi – тензор напруг (для твердих частинок – це напруги, виникаючі при взаємодії частинок);
R – вектор взаємодії між частинками і газом;
g – прискорення вільного падіння.
Така система добре описує гідродинаміку віброкиплячого шару, та при залученні додаткових емпіричних або напівемпіричних залежностей для Кi і R дозволить чисельно розрахувати поля ei, vi і p. Однак ця система відрізняється достатньо високою складністю і з урахуванням характерних особливостей віброкипіння може бути спрощена.
Рівняння руху газу із системи (1) має вигляд:
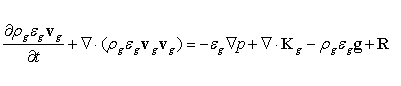 (2)
(2)
Якщо припустити, що за своїми властивостями віброкиплячий шар являє собою проміжну ступінь між нерухомим фільтруючим середовищем і псевдозрідженим шаром, то у цьому випадку можливо спростити систему (1), зневаживши у рівнянні руху газу (2) силами інерції, об’ємними силами та тензором в’язкістних напруг. Тоді рівняння (2) приймає форму закону Дарсі, якщо вектор взаємодії між частинками і газом записати у вигляді:
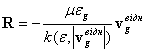 (3)
(3)
та, вочевидь, переходить до закону Дарсі, тобто закону лінійної фільтрації, для низьких чисел Re=degrg![]() /m:
/m:
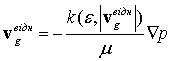 (4)
(4)
де ![]() – відносна швидкість газу;
– відносна швидкість газу;
d – середній діаметр частинок;
m – в’язкість.
Проникність ![]() повинна бути визначена для широкого діапазону значень порізності і критерію Рейнольдса. Для цього необхідно більш глибоко проаналізувати процес фільтрування стосовно до стану віброкипіння.
повинна бути визначена для широкого діапазону значень порізності і критерію Рейнольдса. Для цього необхідно більш глибоко проаналізувати процес фільтрування стосовно до стану віброкипіння.
Намагання отримати макроскопічне рівняння плину газу в нерухомому пористому середовищі шляхом осереднення рівняння нерозривності й лінеаризованого рівняння Нав’є-Стокса по елементарному фізичному об’єму середовища робилися у ряді робіт, наприклад, [11,12]. В результаті автори отримали закон Дарсі, який встановлює лінійний зв’язок між середньою (для малих об’ємів вона еквівалентна фіктивній [12-14]) швидкості плину газу ![]() і градієнтом середнього тиску:
і градієнтом середнього тиску:
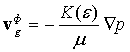 (5)
(5)
Проникність K(e) має розмірність площі; вона не залежить від властивостей рідини і є чисто геометричною характеристикою пористого середовища [15].
Існує багато формул, які виражають K(e) через параметри пористої структури – як чисто емпіричних, так і отриманих на основі моделювання пористої структури. Найбільше розповсюдження отримало рівняння Козені-Кармана [15], яке виведене з аналогії між пористим середовищем і системою капілярів, а також рівняння моделі хвилястих капілярів різного радіусу. Якщо у цих або аналогічних рівняннях замінити величини a (питома поверхня), і ![]() (характерний радіус пор) на їхні середні значення для шару сипкого середовища
(характерний радіус пор) на їхні середні значення для шару сипкого середовища ![]() і
і ![]() [12,14], то проникність для ламінарної фільтрації у загальному вигляді запишеться як:
[12,14], то проникність для ламінарної фільтрації у загальному вигляді запишеться як:
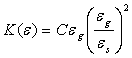 (6)
(6)
де С – деякий коефіцієнт. Його значення можна оцінити у широкому спектрі порізності для нерухомих сипких середовищ. Маємо таку наближену оцінку:
![]() (7)
(7)
і відповідно:
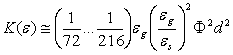 (8)
(8)
де Ф – фактор форми частинок.
Таким чином, в рамках нерухомого фільтруючого середовища ми приходимо до цілком певної нелінійної залежності проникності від порізності.
Для розрахунку падіння тиску в псевдозрідженому шарі широке розповсюдження отримало рівняння Ергана [13,14,16,17]:
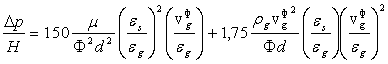 (9)
(9)
В роботі [13] для розрахунку сил взаємодії між частинками і газом у фонтануючих шарах рівняння Ергана розповсюджується на шари безкінечно малих висот, тобто приймалося ![]() , у цьому випадку для невисоких фіктивних швидкостей газу також спостерігається лінійна залежність між швидкістю течії газу і градієнтом тиску, при цьому проникність буде дорівнювати:
, у цьому випадку для невисоких фіктивних швидкостей газу також спостерігається лінійна залежність між швидкістю течії газу і градієнтом тиску, при цьому проникність буде дорівнювати:
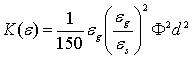 (10)
(10)
що добре узгоджується з (8). Переходячи до дійсної швидкості газу [12-14]
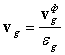 (11)
(11)
яка фігурує у (1)-(3), проникність k(e)=K(e)/eg прийме вигляд:
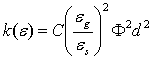 (12)
(12)
Формула (12) придатна при Re=degrg![]() /m<1 і eg<0,8. У випадку, якщо Re>1, можна скористатися векторною модифікацією формули Ергана, наведеною в [14]:
/m<1 і eg<0,8. У випадку, якщо Re>1, можна скористатися векторною модифікацією формули Ергана, наведеною в [14]:
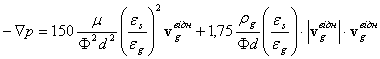 (13)
(13)
Позначимо:
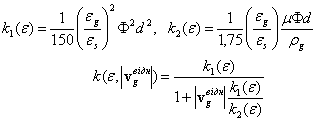 (14)
(14)
тоді рівняння фільтрування запишеться у вигляді:
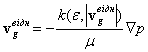 (15)
(15)
що еквівалентно наступній нелінійній системі рівнянь:
 (16)
(16)
Вказана система придатна при eg<0,8 і може бути чисельно вирішена будь-якими итераційними методами. Для порізности eg>0,8 у [15] пропонується формула для градієнта тисків, з якої проникність запишеться:
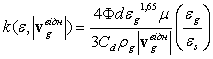 (17)
(17)
де 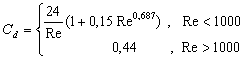
Для поодинокої кулеподібної частинки, яка рухається повільно, eg=1, es=0, і Сd=24/Re, що виражає відомий закон Стокса [13]; для великих значень Re формула (17) відповідає закону Ньютона.
Таким чином, уявлення про віброкиплячий шар як про проміжну ступінь між нерухомим фільтруючим середовищем і псевдозрідженим шаром, дозволяє систему диференціальних рівнянь нерозривності і руху (2) привести до вигляду:
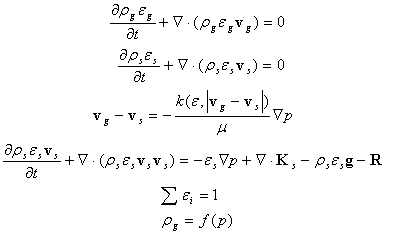 (18)
(18)
де останнє рівняння являє собою рівняння стану газу. За звичайних умов можна скористуватися рівнянням стану ідеального газу:
![]() (19)
(19)
Проникність ![]() визначається у залежності від eg і Re за формулами (12), (15) або (17). Для полегшення запису граничних умов зовнішню вібраційну дію можна врахувати відповідною заміною координат, наприклад, при вертикальних коливаннях вібруючої поверхні за законом s=s(t) необхідно ввести нову координату:
визначається у залежності від eg і Re за формулами (12), (15) або (17). Для полегшення запису граничних умов зовнішню вібраційну дію можна врахувати відповідною заміною координат, наприклад, при вертикальних коливаннях вібруючої поверхні за законом s=s(t) необхідно ввести нову координату:
![]() (20)
(20)
Граничними умовами можна вважати умову прилипання газу до стінок апарату, а у зв’язку з тим, що частинки матеріалу можуть рухатися відносно стінок, необхідно задати умову проковзування твердих частинок біля стінок [18,19]. На поверхні шару задається атмосферний тиск.
Для перевірки адекватності вказаної моделі проведено чисельне рішення отриманої системи (1) в одновимірному випадку без урахування дії стінок апарату з використанням метода скінчених різностей [20,21]. Запис скінчено-різнистних рівнянь здійснюється за допомогою явної і неявної схем. Нелінійні системи вирішувалися стандартним методом Ньютона. Подібна схема забезпечує хорошу стійкість різнистного рішення.
Як приклад нижче наводяться (Рис. 1-6) результати моделювання поведінки шару сипкого матеріалу. Вхідними параметрами є насипна густина rs=1600 кг/м3, середній діаметр частинок d=0,3 мм, початкова висота hо =0,24 м, середня порізність в статичному стані egо=0,4, початкова швидкість ![]() = 0,3 м/с відносно нерухомої несучої поверхні х=0. Фактор форми Ф=0,55. Вихідними параметрами системи є поля eg=eg(x,t), es=es(x,t),
= 0,3 м/с відносно нерухомої несучої поверхні х=0. Фактор форми Ф=0,55. Вихідними параметрами системи є поля eg=eg(x,t), es=es(x,t), ![]() ,
, ![]() ,
, ![]() . Зазначимо, що одновимірна модель дозволяє врахувати високі швидкості фільтрації і вплив фільтруючого середовища на структуру шару, однак вона не враховує взаємодію частинок між собою і зі стінками апарату. Для врахування цих чинників необхідно рішати просторову задачу з залученням додаткових залежностей для запису тензору напруг, який описує ці взаємодії. Один з видів запису компонентів такого тензору вказаний у [7].
. Зазначимо, що одновимірна модель дозволяє врахувати високі швидкості фільтрації і вплив фільтруючого середовища на структуру шару, однак вона не враховує взаємодію частинок між собою і зі стінками апарату. Для врахування цих чинників необхідно рішати просторову задачу з залученням додаткових залежностей для запису тензору напруг, який описує ці взаємодії. Один з видів запису компонентів такого тензору вказаний у [7].
|
|
|
|
|||
|
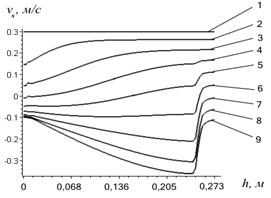
Рис.1 Швидкість твердих частинок по висоті шару: 1–t=0 с; 2–t=0,5×10-2 с; 3– t=1×10-2 с; 4– t=1,4×10-2с; 5 – t = 1,9×10-2 с; 6– t = 2,3×10-2 с; 7– t = 2,8×10-2 с; 8– t = 3,2×10-2 с; 9– t =3,7×10-2 с. |
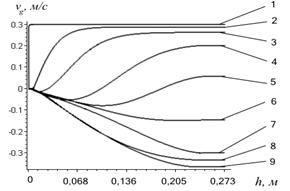
Рис. 2 Швидкість газу по висоті шару: 1– t=0 с; 2– t=0,5×10-2 с; 3– t=1×10-2 с; 4– t=1,4×10-2 с; 5– t =1,9×10-2 с; 6– t =2,3×10-2 с; 7– t =2,8×10-2 с; 8– t =3,2×10-2 с; 9– t =3,7×10-2 с. |
|
|||
|
|
|
||||
|
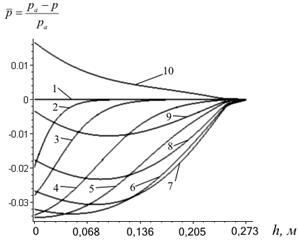
Рис. 3. Розподіл тиску по висоті шару: 1– t=0 с; 2– t=0,2×10-2 с; 3– t=0,5×10-2 с; 4– t=1×10-2 с; 5– t=1,4×10-2 с; 6– t=1,9×10-2 с; 7– t =2,3×10-2 с; 8– t=2,8×10-2 с; 9– t =3,2×10-2 с;10–t=3,7×10-2 с. |
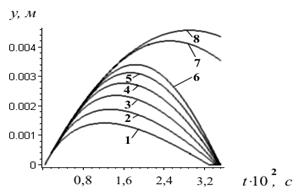
Рис. 4 Траєкторії руху частинок по висоті шару, відраховані від вихідного положення: 1–0 м; 2 – 0,038 м; 3 – 0,075 м; 4 – 0,113 м; 5 – 0,150 м; 6 – 0,188 м; 7 – 0,225 м; 8 – 0,263 м.
|
||||
|
|
|
|
|||
|
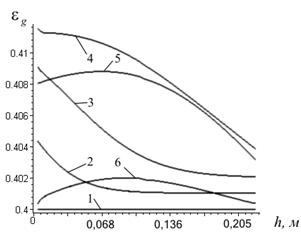
Рис. 5 Розподіл порізності по висоті шару: 1– t =0 с; 2– t =0,5×10-2 с; 3 – t =1×10-2 с; 4– t =1,9×10-2 с; 5 – t =2,8×10-2 с; 6– t =3,6×10-2 с. |
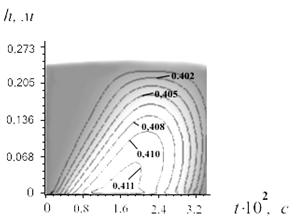
Рис. 6 Розподіл порізності по висоті шару у часі |
|
|||
Як видно з результатів моделювання, у початковий момент процесу підкидання матеріалу рух нижніх моношарів частинок різко сповільнюється (рис. 1), у той час як середні та верхні шари рухаються рівномірно. Газ, що знаходиться в порах матеріалу, в початковий момент (t=0) намагається рухатися разом з шаром, тобто ![]() =0, однак у наступні моменти його швидкість біля несучої поверхні х=0 (де швидкість газу нульова у відповідності з граничною умовою) різко падає (рис. 2), у той самий час відносна швидкість
=0, однак у наступні моменти його швидкість біля несучої поверхні х=0 (де швидкість газу нульова у відповідності з граничною умовою) різко падає (рис. 2), у той самий час відносна швидкість ![]() по модулю зростає – газ починає фільтруватися крізь нижні ділянки шару, сповільнюючи їх. У верхніх ділянках шару газ продовжує рухатися разом з твердими частинками, тобто
по модулю зростає – газ починає фільтруватися крізь нижні ділянки шару, сповільнюючи їх. У верхніх ділянках шару газ продовжує рухатися разом з твердими частинками, тобто ![]() . Під шаром виникає різкий перепад тиску (рис.3), який і є рушійною силою процесу фільтрування газу крізь віброкиплячий шар. Одночасно з цим нерівномірність сповільнення частинок по висоті позначається на порізності шару – у початкові моменти часу в нижніх ділянках шару вона зростає (рис. 5, рис. 6).
. Під шаром виникає різкий перепад тиску (рис.3), який і є рушійною силою процесу фільтрування газу крізь віброкиплячий шар. Одночасно з цим нерівномірність сповільнення частинок по висоті позначається на порізності шару – у початкові моменти часу в нижніх ділянках шару вона зростає (рис. 5, рис. 6).
Описаний процес у подальшому захоплює (з цілком певною швидкістю) наступні ділянки, сягаючи верху шару, однак частинки, які знаходяться внизу шару, як це видно з рис. 1 і рис. 4, починають своє зниження раніше верхніх. В результаті процес розповсюдження збурювань по шару стає аналогічним процесу розповсюдження нелінійної хвилі деформації у деякому псевдонерухомому суцільному середовищі з особливою реологією (рис. 5, рис. 6). Як наслідок, висота підйому частинок (деформація) не однакова по координаті шару (рис. 4). Верх шару має максимальне переміщення ![]() мм, нижні ж частинки мають переміщення тільки
мм, нижні ж частинки мають переміщення тільки ![]() мм. Подібний розкид залежить від проникності шару, його насипної густини, зовнішнього тиску, внутрішніх чинників. Для деяких шарів може виникнути ситуація, коли
мм. Подібний розкид залежить від проникності шару, його насипної густини, зовнішнього тиску, внутрішніх чинників. Для деяких шарів може виникнути ситуація, коли ![]() , і помітний відрив виникає у деякій точці х>0, що описано на початку статті. В цьому разі процеси у нижній зоні не будуть відповідати вимогам технологічного процесу.
, і помітний відрив виникає у деякій точці х>0, що описано на початку статті. В цьому разі процеси у нижній зоні не будуть відповідати вимогам технологічного процесу.
Таким чином, для апаратів з віброкиплячим шаром як об’єктів управління, необхідна ретельна перевірка режимів роботи на основі вказаної моделі по визначенню можливої наявності недопустимих зон віброзрідження, відкликів на зміну вхідних параметрів та можливого виходу системи за межі гранично припустимих режимів роботи.
In this work is researched modeling of hydrodynamics vibratory boiling layers of loose materials. The mathematical model of the motion layer is offered with take-off from carrying surfaces. This model is used for the numerical calculation of the fields of the velocities, pressures and porosity for univariate problem.
1. Хобин В.А., Степанов М.Т. Алгоритмы гарантирующего управления с прогнозированием // Техніка в сільськогосподарському виробництві, галузеве машинобудування, автоматизація: Зб. наук. пр. / Кіровоград. держ. техн. ун-т. – Кіровоград, 2002.-Вип. 11.- С.163-166.
2. Членов В.А., Михайлов Н.В. Виброкипящий слой. - М.: Наука, 1972. – 343 с.
3. Каталымов А.В., Любартович В.А. Дозирование сыпучих и вязких материалов. - Л.: Химия, 1990. – 240 с.
4. Вибрации в технике. Справочник: В 6 т.- М.: Машиностроение, 1981. - Т.4. – 509 с.
5. Kroll W. Fliesserscheinungen auf Haufwerken in schwingenden Gefassen // Chemic Ingenieur Technik. – 1955. - №1. – P. 142-148.
6. Блехман И.И. Джанелидзе Г.Ю. Вибрационное перемещение. – М.: Наука, 1964. – 410 с.
7. Gidaspow, D. Multiphase flow and fluidization: Continuum and kinetic theory descriptions. - Boston: Academic Press Inc., – 1994. – 211 p.
8. Huilin, L., S. Yongli, L. Yang, H. Yurong and J. Bouillard, Numerical simulations of hydrodynamic behavior in spouted beds // Trans. Inst. Chem. Eng.. - 2001 - 79, P..593-599.
9. Гидротранспорт. Вопросы гидравлики. / Н.А.Силин, Ю.К.Витошкин, В.М.Карасик, В.Ф.Очеретько. – К.: Наукова Думка, 1971. – 227 с.
10. Дейч М.Е., Филиппов Г.А. Газодинамика двухфазных сред. – М.: Энергия, 1968. – 424 с.
11. Whiteker S. – Ind. Eng. Chem., 1969, v. 34, P. 248-252.
12. Kozicki W., Hsu C.J., Tiu C. Non-newtonian flow through packed beds and porous media. // Chem. Engng. Sci., - 1967. - 22, №4, P.487-502.
13. Касаткин А.Г. Основные процессы и аппараты химической технологии. - М.: Химия, 1973.–752с.
14. Wen, C. Y. and Y. H. Yu. Mechanics of fluidization // Chem. Eng. Prog. Symp. - 1966. - Series, 62, P.100-106.
15. Хейфец Л.И., Неймарк А.В. Многофазные процессы в пористых средах. - М.: Химия, 1982.–320с.
16. Кунии Д., Левеншпиль О. Промышленное псевдоожижение. Перевод с английского. – М.: Химия, 1976. – 448 с.
17. Лукьянов П.И. Аппараты с движущимся зернистым слоем. – М.: Машиностроение, 1973. – 182 с.
18. Литвинов В.Г. Движение нелинейно-вязкой жидкости. – М.: Наука, 1982. – 376 с.
19. Раскин Х.И. Применение методов физической кинетики к задачам вибрационного воздействия на сыпучие среды//ДАН СССР 1975. - т.220, №1, - с.54-57.
20. Математика и САПР: В 2-х кн. Кн.2. Пер. с франц.// Жермен-Лакур П.,Жорж П.Л., Пистр Ф., Безье П. - М.: Мир, 1989. –264 с.
21. Самарский А.А. Введение в теорию разностных схем. – М.: Наука, 1966. – 632 с.
Ответы на вопросы [_Задать вопроос_]
Читайте также
Моделирование объектов и систем управления
Соколов А.Е., Махова Е.О. Моделирование процесса принятия педагогического решения при компьютеризированном обученииСлавко О.Г. Порівняльний аналіз керування регулятором на основі локальної моделі керованого процесу та П-регулятором
Войтенко В.В., Дикусар Е.В, Ситников В.С. Определение частоты среза устройства сглаживания данных на основе метода скользящего среднего
Передерій В.І. Алгоритм визначення та оцінки характеристик ефективності комп’ютерних систем на початковій стадії проектування в умовах невизначенності
Ляшенко С.А, Ляшенко А.С. Оценка модели псевдолинейной регрессии
Ладієва Л.Р. Математична модель процесу газової мембранної дистиляції
Носов П.С., Косенко Ю.І. Нечіткі моделі і методи ідентифікації та прогнозу стану інформаційної моделі студента
Китаев А.В., Глухова В.И. Анализ работы синхронного двигателя с неявнополюсным ротором по данным каталога
Дорошкевич В.К., Пироженко А.В., Хитько А.В., Хорольский П.Г. К определению требований к системам увода космических объектов
Голінко І.М., Ковриго Ю.М., Кубрак А.І. Настройка системи керування за імпульсною характеристикою об’єкта
Яшина К.В., Садовой А.В. Комплексная математическая модель тепловых процессов, происходящих в дуговых электросталеплавильных печах
Шейник С.П., Рудакова А.В. Использование функций принадлежности для моделирования параметров распределенных объектов
Хомченко А.Н., Литвиненко Е.И. Метод барицентрического усреднения граничных потенциалов электростатического поля
Селяков Е. Б. Моделирование требований к техническим системам методами математической логики
Тодорцев Ю.К., Ларіонова О.С., Бундюк А.М. Математична модель контура теплопостачання когенераційної енергетичної установки
Кириллов О.Л. , Якимчук Г.С. Моделирование процесса управления системой перегрузки углеводородных жидких топлив
Шеховцов А.Н., Козел В.Н. Построение математической модели формирования распределенных систем
Китаев А.В., Глухова В.И. Анализ поведения генератора постоянного тока по данным каталога
Хомченко А.Н., Козуб Н.О. Задачі наближення функцій: від лагранжевих до серендипових поліномів
Хобин В.А., Титлова О.А. Определение температуры парожидкостной смеси в дефлегматоре АДХМ по результатам измерений температуры его поверхности
Григорова Т.М., Усов А.В. Вероятностно-статистическое моделирование маршрутизированных пассажиропотоков в крупных городах
Горач О.О., Тернова Т.І. Моделювання технологічного процесу одержання трести при використані штучного зволоження з урахуванням складу мікрофлори
Дубік Р.М., Ладієва Л.Р. Математична модель розділення неоднорідних рідких систем
Казак В.М, Лейва Каналес Родриго, Яковицкая Е.Ю. Моделирование динамики полета магистрального самолета на исследовательском стенде
Завальнюк И.П. Исследование процесса торможения автомобиля как критического режима динамической системы
Дмитриев С.А., Попов А.В. Построение портрета неисправностей проточной части газотурбинного двигателя на примере АИ-25
Русанов С.А., Луняка К.В., Клюєв О.І., Глухов Г.М. Математичне моделювання робочого процесу в апаратах з віброкиплячим шаром та розробка систем автоматизованого моделювання гідродинаміки віброкиплячих шарів
Боярчук В.П., Сыс В.Б. Экспериментальные исследования влияния технологии шлихтования на изменение жесткости текстильных нитей
Селін Ю.М. Використовування контекстних марківських моделей для аналізу дії промислових вибухів на будівельні конструкції
Рудакова А.В. Проблемы интеграции сложных систем
Передерій В.І., Касап А.М. Математична модель та алгоритм автоматизації розрахунку параметрів комп’ютеризованих систем працюючих у реальному часі
Передерий В.И., Еременко А.П. Математические модели и алгоритмы принятия релевантных решений пользователями автоматизированных систем с учетом личностных и внешних факторов на базе генетических алгоритмов
Михайловская Т.В., Михалев А.И., Гуда А.И. Исследование правил клеточных автоматов для моделирования процессов затвердевания квазиравновесных бинарных сплавов
Хомченко А.Н., Колесникова Н.В. Явление «сверхсходимости» в задаче Прандтля для уравнения Пуассона
Китаев А.В., Глухова В.И. Анализ работы трансформатора по данным каталога
Квасницкий В.В., Ермолаев Г.В., Матвиенко М. В., Бугаенко Б.В., Квасницкий В.Ф. Оценка применимости метода компьютерного моделирования к исследованию напряженно-деформиррованного состояния цилиндрических узлов
Китаев А.И., Глухова В.И. Анализ работы асинхронного двигателя по данным каталога
Шелестов А.Ю Имитационная модель взаимодействия GRID-узлов с очередью доступа к общей памяти
Chizhenkova R.A. Mathematical Aspects of Bibliometrical Analysis of Neurophysiological Investigations of Action of Non-ionized Radiation (Medline-Internet)
Хомченко А.Н., Козуб Н.А. Геометрическое моделирование дискретных элементов с криволинейными границами
Славич В.П. Модель автоматизованої системи управління потоками транспортних засобів
Маркута О.В., Мысак В.Ф. Программная реализация и исследование особенностей метода группового учета аргументов
Степанкова Г.А., Баклан І.В. Побудова гібридних моделей на основі прихованих марківських моделей та нейронних мереж
Бакшанська Т.Д., Рижиков Ю.Г., Тодорцев Ю.К. Математична модель процесу горіння природного газу з рециркуляцією продуктів згорання для цілей управління
Хомченко А.Н. Новые решения обобщенной задачи Бюффона
Передерий В.И., Еременко А.П. Математические модели и алгоритмы определения релевантности принимаемых решений с учетом психофункциональных характеристик пользователей при управлении автоматизированными динамическими системами
Ложечников В.Ф., Михайленко В.С., Максименко И.Н. Аналитическая много режимная математическая модель динамики газовоздушного тракта барабанного котла средней мощности
Ковриго Ю.М., Фоменко Б.В., Полищук И.А. Математическое моделирование систем автоматического регулирования с учетом ограничений на управление в пакете Matlab
Исаев Е.А., Наговский Д.А. Математическое описание влияния кривизны контактирующих тел на угол смачивания жидкости в межчастичном пространстве
Бідюк П.І., Литвиненко В.І., Кроптя А.В. Аналіз ефективності функціонування мережі Байєса
Тищенко И.А., Лубяный В.З. Математическое моделирование вокодера для определения оптимальной формы импульса сигнала возбуждения.
Николаенко Ю.И., Моисеенко С.В. Моделирование гармонического полиномиального базиса гексагона.
Козуб Н.А., Манойленко Е.С., Хомченко А.Н. Температурный тест для модифицированных базисов бикубической интерполяции.
Клименко А.К. Об упрощенном численном конструировании обратной модели динамического объекта.
Китаев А.В., Сушич Е.Ф. Расчет погрешностей измерительных трансформаторов.
Передерій В.І.,Касап А.М. Математична модель та алгоритм автоматизації розрахунку параметрів комп’ютеризованих систем працюючих у реальному часі
Шпильовий Л.В. Математична модель та алгоритм екстремального управління процесом осадження дисперсної фази суспензії.
Тулученко Г.Я. Інформаційний модуль експрес-пошуку точок еквівалентності процесу нейтралізації.
Тернова Т.І. Урахування морфогенетичного рівняння в математичній моделі тканини.
Попруга А.Г. Теоретические и экспериментальные исследования электрических нагревателей по критерию экономии энергии.