УДК 656.13
ВЕРОЯТНОСТНО-СТАТИСТИЧЕСКОЕ МОДЕЛИРОВАНИЕ МАРШРУТИЗИРОВАННЫХ ПАССАЖИРОПОТОКОВ В КРУПНЫХ ГОРОДАХ
Григорова Т.М., Усов А.В.
Введение
Основной способ транспортировки пассажиров в пределах больших городов Украины – маршрутизированный транспорт. В последнее время увеличивается количество маршрутов и интенсивность движения транспорта, что способствует лучшему обслуживанию пассажиров. Однако увеличение интенсивности работы транспорта приводит к ухудшению экологической обстановки, повышает опасность перегрузки дорог, а увеличение количества маршрутов приводит к излишней конкуренции между водителями за пассажиров, что снижает безопасность движения.
Улучшение качества обслуживания, при перевозке пассажиров – одна из самых важных услуг, оказываемых транспортом. Одним из важных параметров качества обслуживания пассажиров является потеря пассажирочаса – это количество денег, которое пассажир готов отдать, чтобы сэкономит единицу времени. К настоящему времени существует три основных подхода к определению пассажирочаса [1]. При этом авторы исходят из:
- национального дохода или чистой продукции, созданных за один человеко-час;
- среднечасовой заработок;
- субъективной оценки пассажиром своего времени.
В данной статье рассмотрена Т-В модель, позволяющая исследовать оптимальные интервалы движения транспорта по одному маршруту с учетом затрат времени пассажиров. Причем при моделировании учтено, что большинство пассажиропотоков могут быть перевезены с помощью транспортных средств конкурирующих маршрутов. С увеличением интервала движения транспортных средств по данному маршруту возрастают затраты времени пассажиров, но сокращаются транспортные расходы и наоборот, при снижении интервала движения сокращаются затраты времени пассажиров, но увеличиваются расходы транспорта.
Целью моделирования является компромисс между социально-экономической значимостью пассажирских перевозок и расходами пассажирского транспорта.
Постановка задачи
Для того, чтобы грамотно организовать работу пассажирского транспорта, необходимо иметь информацию о пассажирских потоках, т.е. потребности пассажиров в перевозке с одного установочного пункта на другой.
Для решения задачи определения продолжительности временных интервалов между транспортными средствами на каждом маршруте требуется следующая информация:
- набор остановочных пунктов, по которым движутся транспортные средства и перемещаются пассажиры;
- для каждого маршрута должно быть определено, между какими остановочными пунктами он может перевести пассажиров;
- потребность пассажиров в перевозке с каждой остановки на другую (количество пассажиров, поступающих на каждый остановочный пункт, чтобы переместиться на другой установочный пункт, чтобы переместиться на другой остановочный пункт в единицу времени);
- средняя стоимость единицы времени, потерянной пассажиром на остановочном пункте в ожидании транспорта;
- себестоимость одного рейса транспортного средства на каждом маршруте.
Используя данную информацию, построим математическую модель оптимизации интервалов движения городского пассажирского транспорта.
Для того, чтобы перейти к математической постановке задачи, необходимо описать переменные и параметры, входящие в модель. Определить область их существования, чтобы задача была корректной и разрешимой. Основная модель, используемая для описания транспортных и пассажирских потоков [3] – Пуассоновский поток.
![]() - количество остановочных пунктов, по которым движутся транспортные средства и перемещаются пассажиры (
- количество остановочных пунктов, по которым движутся транспортные средства и перемещаются пассажиры (![]() ).
).
![]() - количество маршрутов, по которым передвигаются транспортные средства (
- количество маршрутов, по которым передвигаются транспортные средства (![]() ).
).
![]() - себестоимость одного рейса транспортного средства на k-м маршруте (
- себестоимость одного рейса транспортного средства на k-м маршруте (![]() ).
).
![]() - принимает значение 1, если k-му маршруту можно переехать с i-го остановочного пункта на J-й, иначе принимает значение 0 (
- принимает значение 1, если k-му маршруту можно переехать с i-го остановочного пункта на J-й, иначе принимает значение 0 (![]() )
)
![]() - переменная, описывающая интенсивность пуассоновского потока транспортных средств, движущихся по маршруту в единицу времени (
- переменная, описывающая интенсивность пуассоновского потока транспортных средств, движущихся по маршруту в единицу времени (![]() ).
).
![]() - интенсивность пуассоновского потока пассажиров, поступающих на i-й остановочный пункт с желанием переехать на на маршрутном транспортном средстве на остановочный j-й пункт в единицу времени поступления (
- интенсивность пуассоновского потока пассажиров, поступающих на i-й остановочный пункт с желанием переехать на на маршрутном транспортном средстве на остановочный j-й пункт в единицу времени поступления (![]() )/
)/
![]() - стоимость единицы времени (пассажирочаса), потерянной пассажиром в ожидании транспорта на остановочном пункте.
- стоимость единицы времени (пассажирочаса), потерянной пассажиром в ожидании транспорта на остановочном пункте.
Для того, чтобы обеспечить потребность каждого пассажира в перевозке, должны существовать маршруты, способные перевести пассажира между его начальным и конечным остановочными пунктами. Т.е. если ![]() то
то ![]() .
.
Математическая постановка задачи
Очевидно, что интенсивность потоков транспортных средств, движущихся по каждому маршруту не отрицательна:
![]() (1)
(1)
Затраты городского пассажирского транспорту на перевозку составят:
![]() (2)
(2)
Подсчитаем общую интенсивность потока транспорта, поступающего на i-й остановочный пункт для перевозки на j-й остановочный пункт:
![]() (3)
(3)
Выведем формулу среднего времени, теряемого одним пассажиром в ожидании транспорта, на примере системы массового обслуживания (рис.1).
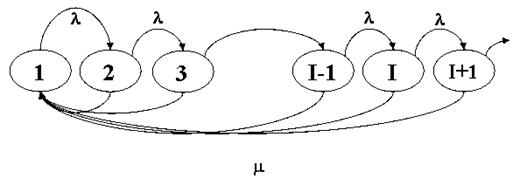
Рис.1 Процесс убыли увеличения
В данном случае ![]() - суммарная интенсивность потоков пассажиров, а
- суммарная интенсивность потоков пассажиров, а ![]() - интенсивность потока транспорта.
- интенсивность потока транспорта. ![]() - вероятность , что на остановочном пункте находится l пассажиров (
- вероятность , что на остановочном пункте находится l пассажиров (![]() ). Система уравнений, описывающих равновесие при поиске
). Система уравнений, описывающих равновесие при поиске ![]() имеет вид [5]
имеет вид [5]
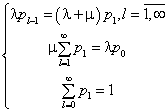 (4)
(4)
Решением данной системы является:
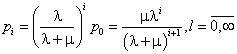 (5)
(5)
Среднее количество пассажиров на остановочном пункте:
![]() (6)
(6)
Таким образом, воспользовавшись (3,6), получим среднее количество пассажиров, ожидающих транспорта на i-м остановочном пункте для переезда на j-й:
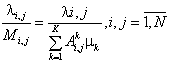
Тогда средние затраты пассажиров ожидающих транспорта на i-ом остановочном пункте для переезда на j-й в единицу времени:
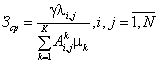 (7)
(7)
Целевой функцией в данной задаче являются суммарные затраты транспорта на передвижение транспортных средств по маршрутам в единицу времени (2) и потери времени пассажиров в ожидании (7):
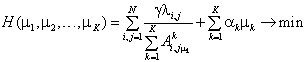 (8)
(8)
Пусть ![]() - решение задачи (1-8). Тогда расходы транспорта и пассажиров совпадают в этой точке.
- решение задачи (1-8). Тогда расходы транспорта и пассажиров совпадают в этой точке.
По необходимому условию экстремума производные от целевой функции по каждому направлению равны нулю:
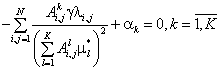 (9)
(9)
Выразив ![]() из (9), подставим в (2) и получим необходимый результат:
из (9), подставим в (2) и получим необходимый результат:
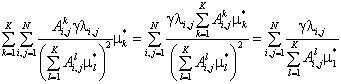 (10)
(10)
Покажем, что целевая функция (9) выпукла вниз на всей области существования. Для этого посмотрим квадратичную форму, составленную из вторых производных.
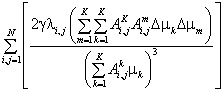 (11)
(11)
Квадратичная форма положительно определена, т.к. содержит только положительные коэффициенты.
Квадратичная форма (11) положительно определена на всей допустимой области, следовательно, необходимое условие экстремума (равенство градиента целевой функции нулю) являеться и достаточным для глобального экстремума. Для поиска решения данной задачи разработано множество алгоритмов [5]: метод покоординатного спуска, метод Ньютона и т.д. Выпуклость критерия (8) и дифференцируемость на всей допустимой области позволяют решать задачи высокой размерности.
Численный пример для двух маршрутов
Опишем пассажиропотоки с помощью следующих обозначений:
![]() - интенсивность потока пассажиров, перевозимых транспортными средствами только первого маршрута.
- интенсивность потока пассажиров, перевозимых транспортными средствами только первого маршрута.
![]() - интенсивность потока пассажиров, перевозимых транспортными средствами только второго маршрута.
- интенсивность потока пассажиров, перевозимых транспортными средствами только второго маршрута.
![]() - интенсивность потока пассажиров, перевозимых транспортными средствами первого и второго маршрутов.
- интенсивность потока пассажиров, перевозимых транспортными средствами первого и второго маршрутов.
Исходя из того, что потоки транспортных средств пуассоновские, но зависящие друг от друга и от потоков пассажиров, то доля пассажиропотока, перевозимого каждым маршрутом, пропорциональна его интенсивности движения. Поэтому средние потери времени пассажиров в единицу времени на первом маршруте:
![]()
На втором маршруте:
![]()
Рассчитываем оптимальные интервалы движения транспорта при условии:
![]() (12)
(12)
Целевая функция состоит из затрат пассажиров и транспорта:
![]() (13)
(13)
Т.к. квадратичная форма, составленная из вторых производных, отрицательно определена на всей области определения, то достаточным условием экстремума является равенство производных по каждой переменной нулю в точке оптимума:
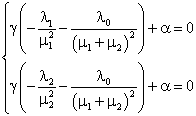 (14)
(14)
Решив систему (14), получим оптимальную точку:
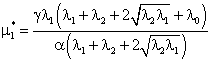 (15)
(15)
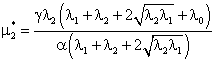 (16)
(16)
При нарушении условий (11) не удается получить оптимальные интервалы движения в аналитической форме. Необходимо численно решать задачу оптимизации. Для чего воспользуемся методом Ньютона [4]:
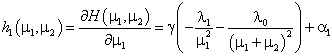 (17)
(17)
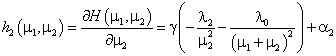 (18)
(18)
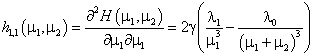 (19)
(19)
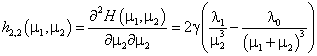 (20)
(20)
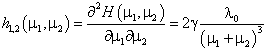 (21)
(21)
Определитель матрицы составленной из вторых производных имеет вид:
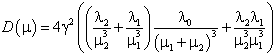 (22)
(22)
Запишем итерационный алгоритм Ньютона по k:
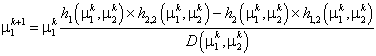 (23)
(23)
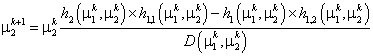 (24)
(24)
Рассмотрим задачу при следующих исходных данных. Общий поток пассажиров, перевозимый двумя маршрутами, составляет ![]() человек в час. Поток пассажиров, перевозимых первым маршрутом,
человек в час. Поток пассажиров, перевозимых первым маршрутом, ![]() , а вторым -
, а вторым - ![]() . Стоимость проезда по одному маршруту составляет
. Стоимость проезда по одному маршруту составляет ![]() и
и ![]() соответственно. Потери пассажирочаса составляют
соответственно. Потери пассажирочаса составляют ![]() .
.
На рис.2 представлена целевая функция на плоскости двух переменных.


Рис. 2 Суммарные затраты транспорта и пассажиров
Рассмотрим результаты, полученные с помощью итераций метода Ньютона, рассчитанные по (14-21).
Таблица 1
Реализация метода Ньютона
|
ķ |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
μ1 |
1 |
1,4730 |
2,1232 |
2,9264 |
3,7128 |
4,1871 |
4,2982 |
4,3028 |
4,30028 |
|
μ2 |
1 |
1,4710 |
2,1141 |
2,8972 |
3,6404 |
4,0610 |
4,1484 |
4,1514 |
4,1514 |
В этих условиях оптимальные затраты транспорта составляют ~21,21грн.в час при интенсивностях движения μ1~ 4,302 и μ2~ 4,151.Среднее количество перевозимых пасажиров 50 для первого маршрута и 39 для второго за рейс. При стоимости проезда в 2 грн, прибыльность первого маршрута 100, а второго 39грн. за рейс.
Заключение
Основным достоинством данной модели является возможность одновременно определять оптимальный режим работы транспорта на большом количестве маршрутов с учетом потерь пассажиров при ожидании на остановочных пунктах. Что позволит эффективно управлять транспортными потоками в мегаполисе...
Недостатком является то. что не учитывается ограничение на пассажировместимость транспортных средств. Но на практике пассажирский транспорт обычно перегружается лишь в часы пик. Для того, чтобы компенсировать перегрузку транспорта в часы пик стоимость пассажирочаса в это время в 1.5-2 раза выше, чем в обычное время.
Поэтому построенная модель может быть эффективно использована при планировании работы городского маршрутизированного транспорта, учитывая социально-экономический эффект для пассажиров, и меняющиеся в течение суток пассажиропотоки.
The theoretical-probabilistic model of optimization of duration of time domains is considered between transport vehicles, locomotive on every route. A design purpose is minimization of total charges of transport on transportations and losses of time of passengers. At the puassonovskikh streams of passengers and transport a criterion is accepted by the type of the protuberant differentiated function. An example is resulted for two routes.
1. Аррак А.О. Социально-экономическая эффективность пассажирских перевозок. Таллинн: Ээсти раамат, 1982.
2. Пчелицев О.С. Экономическая оценка времени населения и ее использование при определении требований к развитию транспортной инфраструктуры, в кн. Развиние системы пассажирских сообщений. М.: Наука, 1980.
3. Лигум Ю.С. Автоматизированные системы управления технологическими процессами пассажирского автомобильного транспорта. К.: Тэхника, 1989.
4. Базара М. Шетти К. Нелинейное программирование. Теория и алгоритмы. М.: Мир, 1982.
5. Григоров М.А, Дащенко А.Ф, Усов А.В. Проблемы моделирования и управления движением транспортных потоков в крупных городах. Одесса,: Астропринт, 2004.-272 с.
Ответы на вопросы [_Задать вопроос_]
Читайте также
Моделирование объектов и систем управления
Соколов А.Е., Махова Е.О. Моделирование процесса принятия педагогического решения при компьютеризированном обученииСлавко О.Г. Порівняльний аналіз керування регулятором на основі локальної моделі керованого процесу та П-регулятором
Войтенко В.В., Дикусар Е.В, Ситников В.С. Определение частоты среза устройства сглаживания данных на основе метода скользящего среднего
Передерій В.І. Алгоритм визначення та оцінки характеристик ефективності комп’ютерних систем на початковій стадії проектування в умовах невизначенності
Ляшенко С.А, Ляшенко А.С. Оценка модели псевдолинейной регрессии
Ладієва Л.Р. Математична модель процесу газової мембранної дистиляції
Носов П.С., Косенко Ю.І. Нечіткі моделі і методи ідентифікації та прогнозу стану інформаційної моделі студента
Китаев А.В., Глухова В.И. Анализ работы синхронного двигателя с неявнополюсным ротором по данным каталога
Дорошкевич В.К., Пироженко А.В., Хитько А.В., Хорольский П.Г. К определению требований к системам увода космических объектов
Голінко І.М., Ковриго Ю.М., Кубрак А.І. Настройка системи керування за імпульсною характеристикою об’єкта
Яшина К.В., Садовой А.В. Комплексная математическая модель тепловых процессов, происходящих в дуговых электросталеплавильных печах
Шейник С.П., Рудакова А.В. Использование функций принадлежности для моделирования параметров распределенных объектов
Хомченко А.Н., Литвиненко Е.И. Метод барицентрического усреднения граничных потенциалов электростатического поля
Селяков Е. Б. Моделирование требований к техническим системам методами математической логики
Тодорцев Ю.К., Ларіонова О.С., Бундюк А.М. Математична модель контура теплопостачання когенераційної енергетичної установки
Кириллов О.Л. , Якимчук Г.С. Моделирование процесса управления системой перегрузки углеводородных жидких топлив
Шеховцов А.Н., Козел В.Н. Построение математической модели формирования распределенных систем
Китаев А.В., Глухова В.И. Анализ поведения генератора постоянного тока по данным каталога
Хомченко А.Н., Козуб Н.О. Задачі наближення функцій: від лагранжевих до серендипових поліномів
Хобин В.А., Титлова О.А. Определение температуры парожидкостной смеси в дефлегматоре АДХМ по результатам измерений температуры его поверхности
Горач О.О., Тернова Т.І. Моделювання технологічного процесу одержання трести при використані штучного зволоження з урахуванням складу мікрофлори
Дубік Р.М., Ладієва Л.Р. Математична модель розділення неоднорідних рідких систем
Казак В.М, Лейва Каналес Родриго, Яковицкая Е.Ю. Моделирование динамики полета магистрального самолета на исследовательском стенде
Завальнюк И.П. Исследование процесса торможения автомобиля как критического режима динамической системы
Дмитриев С.А., Попов А.В. Построение портрета неисправностей проточной части газотурбинного двигателя на примере АИ-25
Русанов С.А., Луняка К.В., Клюєв О.І., Глухов Г.М. Математичне моделювання робочого процесу в апаратах з віброкиплячим шаром та розробка систем автоматизованого моделювання гідродинаміки віброкиплячих шарів
Боярчук В.П., Сыс В.Б. Экспериментальные исследования влияния технологии шлихтования на изменение жесткости текстильных нитей
Селін Ю.М. Використовування контекстних марківських моделей для аналізу дії промислових вибухів на будівельні конструкції
Рудакова А.В. Проблемы интеграции сложных систем
Передерій В.І., Касап А.М. Математична модель та алгоритм автоматизації розрахунку параметрів комп’ютеризованих систем працюючих у реальному часі
Передерий В.И., Еременко А.П. Математические модели и алгоритмы принятия релевантных решений пользователями автоматизированных систем с учетом личностных и внешних факторов на базе генетических алгоритмов
Михайловская Т.В., Михалев А.И., Гуда А.И. Исследование правил клеточных автоматов для моделирования процессов затвердевания квазиравновесных бинарных сплавов
Хомченко А.Н., Колесникова Н.В. Явление «сверхсходимости» в задаче Прандтля для уравнения Пуассона
Китаев А.В., Глухова В.И. Анализ работы трансформатора по данным каталога
Квасницкий В.В., Ермолаев Г.В., Матвиенко М. В., Бугаенко Б.В., Квасницкий В.Ф. Оценка применимости метода компьютерного моделирования к исследованию напряженно-деформиррованного состояния цилиндрических узлов
Китаев А.И., Глухова В.И. Анализ работы асинхронного двигателя по данным каталога
Шелестов А.Ю Имитационная модель взаимодействия GRID-узлов с очередью доступа к общей памяти
Chizhenkova R.A. Mathematical Aspects of Bibliometrical Analysis of Neurophysiological Investigations of Action of Non-ionized Radiation (Medline-Internet)
Хомченко А.Н., Козуб Н.А. Геометрическое моделирование дискретных элементов с криволинейными границами
Славич В.П. Модель автоматизованої системи управління потоками транспортних засобів
Маркута О.В., Мысак В.Ф. Программная реализация и исследование особенностей метода группового учета аргументов
Степанкова Г.А., Баклан І.В. Побудова гібридних моделей на основі прихованих марківських моделей та нейронних мереж
Бакшанська Т.Д., Рижиков Ю.Г., Тодорцев Ю.К. Математична модель процесу горіння природного газу з рециркуляцією продуктів згорання для цілей управління
Хомченко А.Н. Новые решения обобщенной задачи Бюффона
Передерий В.И., Еременко А.П. Математические модели и алгоритмы определения релевантности принимаемых решений с учетом психофункциональных характеристик пользователей при управлении автоматизированными динамическими системами
Ложечников В.Ф., Михайленко В.С., Максименко И.Н. Аналитическая много режимная математическая модель динамики газовоздушного тракта барабанного котла средней мощности
Ковриго Ю.М., Фоменко Б.В., Полищук И.А. Математическое моделирование систем автоматического регулирования с учетом ограничений на управление в пакете Matlab
Исаев Е.А., Наговский Д.А. Математическое описание влияния кривизны контактирующих тел на угол смачивания жидкости в межчастичном пространстве
Бідюк П.І., Литвиненко В.І., Кроптя А.В. Аналіз ефективності функціонування мережі Байєса
Тищенко И.А., Лубяный В.З. Математическое моделирование вокодера для определения оптимальной формы импульса сигнала возбуждения.
Николаенко Ю.И., Моисеенко С.В. Моделирование гармонического полиномиального базиса гексагона.
Козуб Н.А., Манойленко Е.С., Хомченко А.Н. Температурный тест для модифицированных базисов бикубической интерполяции.
Клименко А.К. Об упрощенном численном конструировании обратной модели динамического объекта.
Китаев А.В., Сушич Е.Ф. Расчет погрешностей измерительных трансформаторов.
Передерій В.І.,Касап А.М. Математична модель та алгоритм автоматизації розрахунку параметрів комп’ютеризованих систем працюючих у реальному часі
Шпильовий Л.В. Математична модель та алгоритм екстремального управління процесом осадження дисперсної фази суспензії.
Тулученко Г.Я. Інформаційний модуль експрес-пошуку точок еквівалентності процесу нейтралізації.
Тернова Т.І. Урахування морфогенетичного рівняння в математичній моделі тканини.
Попруга А.Г. Теоретические и экспериментальные исследования электрических нагревателей по критерию экономии энергии.
Китаев А.В., Сушич Е.Ф. Приложение положений теории дросселя и трансформатора к расчету и анализу электромагнитом переменного тока.