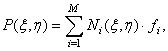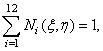УДК 519.3: 518.1
ЗАДАЧІ НАБЛИЖЕННЯ ФУНКЦІЙ: ВІД ЛАГРАНЖЕВИХ ДО СЕРЕНДИПОВИХ ПОЛІНОМІВ
Хомченко А.Н., Козуб Н.О.
Вступ. Задачі наближення функцій займають провідне місце в прикладній математиці. Існує думка, що практично всі прикладні задачі - це задачі теорії наближення функцій (ТНФ). Це означає, що зрештою ці задачі зводяться до визначення функцій, які добре описують процес і легко обчислюються. Способи побудови таких функцій специфічні для різних застосувань математики.
В першу чергу до застосувань ТНФ належать задачі апроксимації спеціальних та елементарних функцій, які важко обчислювати. Наприклад, інтегральний синус, функції Бесселя, тригонометричні та обернені тригонометричні функції, логарифмічна і показникова функції і т.п.
Важливу роль відіграють методи ТНФ в задачах відновлення, які часто виникають в різних прикладних науках: метеорології, геології, топографії і т.п. Задача відновлення полягає в тому, що функція відома на деякій множині точок і треба розробити алгоритм наближеного обчислення функції на більш широкій множині точок. Ці задачі розв’язують за допомогою інтерполяційних методів.
Важко перебільшити значення ТНФ для розробки методів комп’ютерної графіки. Завдяки бурхливому розвитку методу скінченних елементів (МСЕ) в ТНФ і алгоритмах комп’ютерної графіки для наближеного подання функцій (кривих і поверхонь) вже майже 50 років широко використовують кусково-поліноміальні функції одного і багатьох змінних. При цьому в залежності від задачі і бажаної простоти алгоритму користуються кусково-поліноміальними апроксимаціями з різними вимогами гладкості в місцях стиковки поліномів. Підвищений інтерес фахівців саме до поліномів пояснюється не тільки історичними традиціями інтерполяції функцій одного аргументу. Перш за все це привабливі інтерполяційні та обчислювальні властивості поліномів, а також можливість узагальнення для функцій з двома та трьома аргументами.
Наближення функцій багатьох змінних значно складніше, ніж функцій однієї змінної. Це зумовлено не тільки зростанням вимірності задачі, але і низкою принципових труднощів [1]. Саме тому в МСЕ від моменту його виникнення (1943 р.) до появи серендипових елементів (1968 р.) фахівці використовували виключно лагранжеві поліноми в 2D і 3D, які будуються як добуток одновимірних поліномів Лагранжа. При цьому всередині СЕ з’являються «зайві» внутрішні вузли, які лише збільшують обсяг обчислень. Міжелементну неперервність гарантують вузли на контурі СЕ, тому внутрішні вузли лагранжевої інтерполяції можна вилучити, щоб зменшити порядок розв’язувальної системи лінійних алгебраїчних рівнянь. В результаті винахідливої селекції з’явилися перші корисні елементи серендипової сім’ї. Ці елементи більш ефективні з обчислювальної точки зору, але дуже погано піддаються будь-якій формалізації [2].
Особливе значення серендипових СЕ полягає в тому, що при їх конструюванні і дослідженні були знайдені нові ефективні методи, які дали можливість виявити «приховані» параметри інтерполяції. Вперше було доведено, що на відміну від лагранжевих елементів на серендипових елементах існує безліч розв’язків задачі наближення функцій поліномами.
Аналіз попередніх результатів. Історія поліноміальної інтерполяції ![]() починалася з формули Лагранжа (остання чверть 18 століття). Вважається [3], що інтерполяційну формулу Лагранжа першим застосував Варінг. Потім незалежно від Варінга її відкрив Ейлер у 1783 р. Публікація Лагранжа з’явилася у 1795 р. На думку деяких істориків ця формула була відома ще Ньютону (кінець 17 століття). В розвиток теорії поліноміальної інтерполяції функцій однієї змінної зробили свій внесок багато видатних вчених: Гаусс, Стірлінг, Бессель, Еверетт, Вандермонд, Чебишев, Ерміт та інші. Класична формула Лагранжа без будь-яких труднощів узагальнюється на двовимірні області (прямокутники) та тривимірні (прямокутні паралелепіпеди). Цим пояснюється певний інтерес користувачів МСЕ до елементів лагранжевої сім’ї [4]. Перші СЕ серендипової сім’ї були несподівано відкриті у 1968 р. [5], шляхом винахідливого підбору базисних функцій (функцій форми). Згодом ці результати були підтверджені методом оберненої матриці та процедурою Тейлора [6] систематичного генерування функцій форми. Так виникла помилкова впевненість, що задача інтерполяції на серендиповому СЕ має єдиний розв’язок. До речі, на лагранжевих СЕ єдиність розв’язку дійсно має місце. Не дивно, що пошуком альтернативних моделей деякий час ніхто не займався. Альтернативні моделі серендипових СЕ з’явилися у 1982 р. [7], коли для конструювання функцій форми серендипових СЕ був запропонований універсальний ймовірнісно-геометричний метод. В наступних роботах [8-10] були розвинуті саме геометричні аспекти цього підходу і метод став зручним, наочним і простим. Геометричні методи апроксимації функцій поступово витискують традиційні методи матричної алгебри. Це особливо виразно відчувається в МСЕ, де успішно працюють Уачспресс, Маклеод, Барнхілл, а також автори [11].
починалася з формули Лагранжа (остання чверть 18 століття). Вважається [3], що інтерполяційну формулу Лагранжа першим застосував Варінг. Потім незалежно від Варінга її відкрив Ейлер у 1783 р. Публікація Лагранжа з’явилася у 1795 р. На думку деяких істориків ця формула була відома ще Ньютону (кінець 17 століття). В розвиток теорії поліноміальної інтерполяції функцій однієї змінної зробили свій внесок багато видатних вчених: Гаусс, Стірлінг, Бессель, Еверетт, Вандермонд, Чебишев, Ерміт та інші. Класична формула Лагранжа без будь-яких труднощів узагальнюється на двовимірні області (прямокутники) та тривимірні (прямокутні паралелепіпеди). Цим пояснюється певний інтерес користувачів МСЕ до елементів лагранжевої сім’ї [4]. Перші СЕ серендипової сім’ї були несподівано відкриті у 1968 р. [5], шляхом винахідливого підбору базисних функцій (функцій форми). Згодом ці результати були підтверджені методом оберненої матриці та процедурою Тейлора [6] систематичного генерування функцій форми. Так виникла помилкова впевненість, що задача інтерполяції на серендиповому СЕ має єдиний розв’язок. До речі, на лагранжевих СЕ єдиність розв’язку дійсно має місце. Не дивно, що пошуком альтернативних моделей деякий час ніхто не займався. Альтернативні моделі серендипових СЕ з’явилися у 1982 р. [7], коли для конструювання функцій форми серендипових СЕ був запропонований універсальний ймовірнісно-геометричний метод. В наступних роботах [8-10] були розвинуті саме геометричні аспекти цього підходу і метод став зручним, наочним і простим. Геометричні методи апроксимації функцій поступово витискують традиційні методи матричної алгебри. Це особливо виразно відчувається в МСЕ, де успішно працюють Уачспресс, Маклеод, Барнхілл, а також автори [11].
Мета роботи - відстежити трансформацію лагранжевих двовимірних СЕ в СЕ серендипової сім’ї. З’ясувати переваги серендипових СЕ. Підкреслити роль когнітивної комп’ютерної графіки в інформаційних технологіях конструювання стандартних і модифікованих елементів.
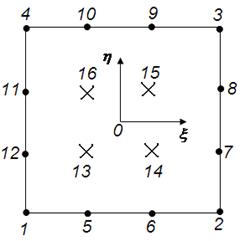
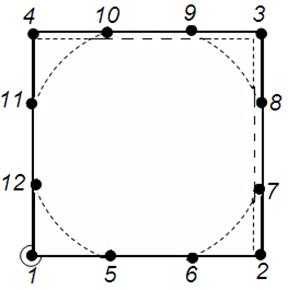
Основна частина. У якості конкретного об’єкта ми розглядаємо двовимірний СЕ бікубічної інтерполяції: лагранжева модель (16 вузлів) і серендипова модель (12 вузлів). На рис.1,а «зайві» внутрішні вузли позначено хрестиками. На рис. 1,б в трикутнику Паскаля пунктиром обмежені 12 доданків інтерполяційного полінома серендипової моделі. В стандартних елементах серендипової сім’ї кількість параметрів інтерполяційного поліному дорівнює кількості вузлів [2,4-6].
|
а) |
б)
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
Рис. 1 До бікубічної інтерполяції: а) дві схеми розташування вузлів; б) фрагмент трикутника Паскаля |
||||||||||||||||||||||||||||||||||||||||||||||||||
Інтерполяційний поліном у формі Лагранжа для функцій ![]() має вигляд:
має вигляд:
|
|
(1) |
де ![]() - функції форми СЕ;
- функції форми СЕ; ![]() відомі значення функції, що інтерполюється; М=16 для лагранжевої моделі; М=12 для серендипової моделі.
відомі значення функції, що інтерполюється; М=16 для лагранжевої моделі; М=12 для серендипової моделі.
Стисло нагадаємо, як будуються функції форми лагранжевої сім’ї. Фактично досить визначити чотири коефіцієнта Лагранжа (за кількістю вузлів у координатному напрямку). Наприклад,
|
|
(2) |
|
|
Якщо у формулах (2) замінити ![]() на
на ![]() отримаємо відповідно
отримаємо відповідно ![]()
![]()
![]() і
і ![]() . Тепер неважко знайти
. Тепер неважко знайти ![]() як добуток відповідних лагранжевих коефіцієнтів однієї змінної. Наприклад,
як добуток відповідних лагранжевих коефіцієнтів однієї змінної. Наприклад,
|
|
Далі за формулою (1) визначається поліном, який має 16 параметрів (рис.1,б).
Для отримання СЕ серендипової сім’ї, треба вилучити внутрішні вузли (рис.1,а) таким чином, щоб не порушити інтерполяційну гіпотезу
|
|
(3) |
зберегти «ваговий» баланс
|
|
(4) |
а також забезпечити міжелементну неперервність (узгодженість). Айронс, Зенкевич та Ергатудіс першими зрозуміли, як це можна зробити. Функції форми, які вони отримали, мають вигляд:
|
|
(5) |
|
|
(6) |
|
|
(7) |
Це стандартний базис СЕ серендипової сім’ї. Назву «серендипова сім’я» запропонував Зенкевич, маючи на увазі несподіваність відкриття цих елементів. Незважаючи на певні недоліки серендипових елементів, фахівці вважають їх корисними і ефективними. Неважко переконатися, що поліноми (5)-(7) забезпечують міжелементну неперервність, а також задовольняють умовам (3) і (4). Відзначимо деякі недоліки стандартного базису:
1) неприродний розподіл по вузлах рівномірної масової сили (наявність від’ємних навантажень в кутових вузлах);
2) надмірна кількість кратних нулів у вузлах, що збільшує «жорсткість» моделі.
Запропоновані попередниками традиційні методи побудови серендипових поліномів не дають можливості встановити причини цих недоліків, а тим більше усунути їх. Треба докорінно змінити підходи до задач наближення функцій поліномами серендипової сім’ї. Нові підходи існують. Математика (особливо прикладна) завжди дає більше, ніж від неї очікують.
Перші спроби дослідити «анатомію» серендипових поліномів (5)-(7) спиралися на відомий метод перерізів. Щоб отримати загальне уявлення про «рельєф» функції форми ![]() досить скористатися перетинаючими площинами
досить скористатися перетинаючими площинами ![]() ,
, ![]() ,
, ![]() Виняткове значення мають ізолінії нульового рівня, які утворюють когнітивний узор в площині носія. Інформативність цього візерунку (особливо для
Виняткове значення мають ізолінії нульового рівня, які утворюють когнітивний узор в площині носія. Інформативність цього візерунку (особливо для ![]() ,
, ![]() ) важко переоцінити. Виявляється, що існує безліч ізоліній, які проходять через вузли на границі СЕ і при цьому зберігають властивості
) важко переоцінити. Виявляється, що існує безліч ізоліній, які проходять через вузли на границі СЕ і при цьому зберігають властивості ![]() . Так народилася гіпотеза про існування альтернативних функцій форми на СЕ вищих порядків. Ця гіпотеза цілком узгоджується з основною теоремою алгебри Гаусса, що додає впевненості і стимулює пошуки нових підходів до конструювання альтернативних поліномів. Перші успіхи в цьому напряму пов’язані з геометричною ймовірністю. На простих СЕ (трикутник: 3 вузли і прямокутник: 4 вузли) ймовірнісний зміст функцій форми був встановлений раніше. Ймовірнісно-геометричний спосіб конструювання функцій форми використовує розбиття складного СЕ на прямокутники і трикутники. В деяких моделях одна сторона трикутника - крива другого порядку. На рис.2 пунктиром зображені лінії нульового рівня функцій
. Так народилася гіпотеза про існування альтернативних функцій форми на СЕ вищих порядків. Ця гіпотеза цілком узгоджується з основною теоремою алгебри Гаусса, що додає впевненості і стимулює пошуки нових підходів до конструювання альтернативних поліномів. Перші успіхи в цьому напряму пов’язані з геометричною ймовірністю. На простих СЕ (трикутник: 3 вузли і прямокутник: 4 вузли) ймовірнісний зміст функцій форми був встановлений раніше. Ймовірнісно-геометричний спосіб конструювання функцій форми використовує розбиття складного СЕ на прямокутники і трикутники. В деяких моделях одна сторона трикутника - крива другого порядку. На рис.2 пунктиром зображені лінії нульового рівня функцій ![]() і
і ![]() стандартного базису бікубічної інтерполяції.
стандартного базису бікубічної інтерполяції.
|
а) |
б) |
|
Рис. 2 Лінії нульового рівня: а) для |
|
Для імовірнісного методу рис.2 дає правило розбиття складного СЕ на прості піделементи. І ще більш важливу роль рис. 2 відіграє в геометричному моделюванні. Аналіз формул (5), (6) (для ![]()
![]() ) та уважне вивчення ізоліній нульового рівня (рис.2) дають нові знання про «анатомію» функцій форми серендипової сім’ї. Є підстави стверджувати, що поверхня
) та уважне вивчення ізоліній нульового рівня (рис.2) дають нові знання про «анатомію» функцій форми серендипової сім’ї. Є підстави стверджувати, що поверхня ![]() конструюється із фрагментів площин і поверхонь другого порядку. Наприклад,
конструюється із фрагментів площин і поверхонь другого порядку. Наприклад, ![]() - це суперпозиція гіперболічного параболоїда (гіпара)
- це суперпозиція гіперболічного параболоїда (гіпара)
|
|
та параболоїда обертання
|
|
До речі, гіпар - це суперпозиція двох площин. Поверхня ![]() конструюється із гіпара
конструюється із гіпара
|
|
і параболічного циліндра
|
|
Існують також інші комбінації.
Щоб автоматизувати процедуру конструювання функцій форми серендипових СЕ, створено каталог площин та поверхонь другого порядку, що проходять через вузли СЕ і точку ![]() Такий каталог і відповідний алгоритм покладено в основу спеціалізованого обчислювального комплексу «SERENDIP», який є прикладом ефективного використання когнітивних функцій комп’ютерної графіки. За допомогою цього комплексу відкриті нові моделі серендипових елементів бікубічної інтерполяції, виявлено «приховані» параметри поліномів. Таким чином, при фіксованій кількості вузлів (12) кількість параметрів бікубічної інтерполяції можна змінювати від 12 до 16. Зрозуміло, що традиційні алгебраїчні методи наближення функцій не охоплюють всі ці випадки.
Такий каталог і відповідний алгоритм покладено в основу спеціалізованого обчислювального комплексу «SERENDIP», який є прикладом ефективного використання когнітивних функцій комп’ютерної графіки. За допомогою цього комплексу відкриті нові моделі серендипових елементів бікубічної інтерполяції, виявлено «приховані» параметри поліномів. Таким чином, при фіксованій кількості вузлів (12) кількість параметрів бікубічної інтерполяції можна змінювати від 12 до 16. Зрозуміло, що традиційні алгебраїчні методи наближення функцій не охоплюють всі ці випадки.
Ізолінії нульового рівня серендипових функцій форми ілюструють несподіваний зв'язок з відомими вузловими лініями, що відкрив експериментально німецький фізик Е.Хладні (1787 р.). Круги Ейлера та фігури Хладні можна вважати першими графічними образами в історії когнітивної графіки.
Висновки. Найбільш плідні застосування модифікованих СЕ стосується апроксимацій, в яких використовують процедуру p-уточнення. В цій процедурі нові ступені волі запроваджуються не шляхом зменшення розмірів СЕ (h-уточнення), а просто додаванням нових мономів вищих порядків. В роботі свідомо фіксується увага переважно на конструктивному аспекті методу, щоб відразу залучити користувачів до практики розробки програм, що реалізують когнітивну функцію комп’ютерної графіки. Прагматична сторона підходу становить особливість і суттєву перевагу роботи - в ній геометричний і обчислювальний аналіз здійснюються просто і наочно.
Possibility of creation of information technology approach of functions with the help serendipian polynoms is considered.
1. Березин И.С. Методы вычислений. / Березин И.С., Жидков Н.П. - М.: Наука, 1966. - Т.1. - 632 с.
2. Зенкевич О. Метод конечных элементов в технике. - М.: Мир, 1975. - 541 с.
3. Джеффрис Г. Методы математической физики / Джеффрис Г., Свирлс Б. - М.: Мир, 1970. - 352 с.
4. Zienkiewicz O.C. The Finite Element Method. V.1: The Basis / Zienkiewicz O.C., Taylor R.L. - Butterworth - Heinemann, 2000. - 689 p.
5. Ergatoudis I. Curved isoparametric, “quadrilateral” elements for finite element analysis / Ergatoudis I., Irons B.M., Zienkiewicz O.C. Int. J. Solids. Struct. - Vol.4. - 1968. - P.31-42.
6. Зенкевич О. Конечные элементы и аппроксимация / Зенкевич О., Морган К. - М.: Мир, 1986. - 318 с.
7. Хомченко А.Н. Некоторые вероятностные аспекты МКЭ / Ив.-Франк. ин-т нефти и газа. Ивано-Франковск, 1982. - 9 с. Деп. в ВИНИТИ 18.03.82, №1213.
8. Хомченко А.Н. О моделировании конечных элементов серендипова семейства / Хомченко А.Н., Камаева Л.И. Прикл. проблемы прочности и пластичности: Всесоюз. межвуз. сб. - Горький: ГГУ, 1985. - С.14-17.
9. Хомченко А.Н. Обратные задачи об интегральных средних для серендиповых полиномов / Хомченко А.Н., Астионенко И.А., Литвиненко Е.И. // Вестн. Херс. нац. техн. ун-та. - 28(2). - Херсон: ХНТУ, 2007. - С. 383-389.
10. Хомченко А.Н. Три способа построения базисов серендиповой интерполяции / Хомченко А.Н., Козуб Н.А. // Математичне та комп’ютерне моделювання. Серія: Фізико-математичні науки. - Вип. 1. - Камянець-Подільский: Кам. - Под. нац. ун-т, 2009. - С.197-202.
11. Митчелл Э. Метод конечных элементов для уравнений с частными производными / Митчелл Э., Уэйт Р. - М.: Мир, 1981. - 216 с.
Ответы на вопросы [_Задать вопроос_]
Читайте также
Моделирование объектов и систем управления
Соколов А.Е., Махова Е.О. Моделирование процесса принятия педагогического решения при компьютеризированном обученииСлавко О.Г. Порівняльний аналіз керування регулятором на основі локальної моделі керованого процесу та П-регулятором
Войтенко В.В., Дикусар Е.В, Ситников В.С. Определение частоты среза устройства сглаживания данных на основе метода скользящего среднего
Передерій В.І. Алгоритм визначення та оцінки характеристик ефективності комп’ютерних систем на початковій стадії проектування в умовах невизначенності
Ляшенко С.А, Ляшенко А.С. Оценка модели псевдолинейной регрессии
Ладієва Л.Р. Математична модель процесу газової мембранної дистиляції
Носов П.С., Косенко Ю.І. Нечіткі моделі і методи ідентифікації та прогнозу стану інформаційної моделі студента
Китаев А.В., Глухова В.И. Анализ работы синхронного двигателя с неявнополюсным ротором по данным каталога
Дорошкевич В.К., Пироженко А.В., Хитько А.В., Хорольский П.Г. К определению требований к системам увода космических объектов
Голінко І.М., Ковриго Ю.М., Кубрак А.І. Настройка системи керування за імпульсною характеристикою об’єкта
Яшина К.В., Садовой А.В. Комплексная математическая модель тепловых процессов, происходящих в дуговых электросталеплавильных печах
Шейник С.П., Рудакова А.В. Использование функций принадлежности для моделирования параметров распределенных объектов
Хомченко А.Н., Литвиненко Е.И. Метод барицентрического усреднения граничных потенциалов электростатического поля
Селяков Е. Б. Моделирование требований к техническим системам методами математической логики
Тодорцев Ю.К., Ларіонова О.С., Бундюк А.М. Математична модель контура теплопостачання когенераційної енергетичної установки
Кириллов О.Л. , Якимчук Г.С. Моделирование процесса управления системой перегрузки углеводородных жидких топлив
Шеховцов А.Н., Козел В.Н. Построение математической модели формирования распределенных систем
Китаев А.В., Глухова В.И. Анализ поведения генератора постоянного тока по данным каталога
Хобин В.А., Титлова О.А. Определение температуры парожидкостной смеси в дефлегматоре АДХМ по результатам измерений температуры его поверхности
Григорова Т.М., Усов А.В. Вероятностно-статистическое моделирование маршрутизированных пассажиропотоков в крупных городах
Горач О.О., Тернова Т.І. Моделювання технологічного процесу одержання трести при використані штучного зволоження з урахуванням складу мікрофлори
Дубік Р.М., Ладієва Л.Р. Математична модель розділення неоднорідних рідких систем
Казак В.М, Лейва Каналес Родриго, Яковицкая Е.Ю. Моделирование динамики полета магистрального самолета на исследовательском стенде
Завальнюк И.П. Исследование процесса торможения автомобиля как критического режима динамической системы
Дмитриев С.А., Попов А.В. Построение портрета неисправностей проточной части газотурбинного двигателя на примере АИ-25
Русанов С.А., Луняка К.В., Клюєв О.І., Глухов Г.М. Математичне моделювання робочого процесу в апаратах з віброкиплячим шаром та розробка систем автоматизованого моделювання гідродинаміки віброкиплячих шарів
Боярчук В.П., Сыс В.Б. Экспериментальные исследования влияния технологии шлихтования на изменение жесткости текстильных нитей
Селін Ю.М. Використовування контекстних марківських моделей для аналізу дії промислових вибухів на будівельні конструкції
Рудакова А.В. Проблемы интеграции сложных систем
Передерій В.І., Касап А.М. Математична модель та алгоритм автоматизації розрахунку параметрів комп’ютеризованих систем працюючих у реальному часі
Передерий В.И., Еременко А.П. Математические модели и алгоритмы принятия релевантных решений пользователями автоматизированных систем с учетом личностных и внешних факторов на базе генетических алгоритмов
Михайловская Т.В., Михалев А.И., Гуда А.И. Исследование правил клеточных автоматов для моделирования процессов затвердевания квазиравновесных бинарных сплавов
Хомченко А.Н., Колесникова Н.В. Явление «сверхсходимости» в задаче Прандтля для уравнения Пуассона
Китаев А.В., Глухова В.И. Анализ работы трансформатора по данным каталога
Квасницкий В.В., Ермолаев Г.В., Матвиенко М. В., Бугаенко Б.В., Квасницкий В.Ф. Оценка применимости метода компьютерного моделирования к исследованию напряженно-деформиррованного состояния цилиндрических узлов
Китаев А.И., Глухова В.И. Анализ работы асинхронного двигателя по данным каталога
Шелестов А.Ю Имитационная модель взаимодействия GRID-узлов с очередью доступа к общей памяти
Chizhenkova R.A. Mathematical Aspects of Bibliometrical Analysis of Neurophysiological Investigations of Action of Non-ionized Radiation (Medline-Internet)
Хомченко А.Н., Козуб Н.А. Геометрическое моделирование дискретных элементов с криволинейными границами
Славич В.П. Модель автоматизованої системи управління потоками транспортних засобів
Маркута О.В., Мысак В.Ф. Программная реализация и исследование особенностей метода группового учета аргументов
Степанкова Г.А., Баклан І.В. Побудова гібридних моделей на основі прихованих марківських моделей та нейронних мереж
Бакшанська Т.Д., Рижиков Ю.Г., Тодорцев Ю.К. Математична модель процесу горіння природного газу з рециркуляцією продуктів згорання для цілей управління
Хомченко А.Н. Новые решения обобщенной задачи Бюффона
Передерий В.И., Еременко А.П. Математические модели и алгоритмы определения релевантности принимаемых решений с учетом психофункциональных характеристик пользователей при управлении автоматизированными динамическими системами
Ложечников В.Ф., Михайленко В.С., Максименко И.Н. Аналитическая много режимная математическая модель динамики газовоздушного тракта барабанного котла средней мощности
Ковриго Ю.М., Фоменко Б.В., Полищук И.А. Математическое моделирование систем автоматического регулирования с учетом ограничений на управление в пакете Matlab
Исаев Е.А., Наговский Д.А. Математическое описание влияния кривизны контактирующих тел на угол смачивания жидкости в межчастичном пространстве
Бідюк П.І., Литвиненко В.І., Кроптя А.В. Аналіз ефективності функціонування мережі Байєса
Тищенко И.А., Лубяный В.З. Математическое моделирование вокодера для определения оптимальной формы импульса сигнала возбуждения.
Николаенко Ю.И., Моисеенко С.В. Моделирование гармонического полиномиального базиса гексагона.
Козуб Н.А., Манойленко Е.С., Хомченко А.Н. Температурный тест для модифицированных базисов бикубической интерполяции.
Клименко А.К. Об упрощенном численном конструировании обратной модели динамического объекта.
Китаев А.В., Сушич Е.Ф. Расчет погрешностей измерительных трансформаторов.
Передерій В.І.,Касап А.М. Математична модель та алгоритм автоматизації розрахунку параметрів комп’ютеризованих систем працюючих у реальному часі
Шпильовий Л.В. Математична модель та алгоритм екстремального управління процесом осадження дисперсної фази суспензії.
Тулученко Г.Я. Інформаційний модуль експрес-пошуку точок еквівалентності процесу нейтралізації.
Тернова Т.І. Урахування морфогенетичного рівняння в математичній моделі тканини.
Попруга А.Г. Теоретические и экспериментальные исследования электрических нагревателей по критерию экономии энергии.
Китаев А.В., Сушич Е.Ф. Приложение положений теории дросселя и трансформатора к расчету и анализу электромагнитом переменного тока.