УДК 519.3:515.2
ТЕМПЕРАТУРНЫЙ ТЕСТ ДЛЯ МОДИФИЦИРОВАННЫХ БАЗИСОВ БИКУБИЧЕСКОЙ ИНТЕРПОЛЯЦИИ
Козуб Н.А., Манойленко Е.С., Хомченко А.Н.
Постановка проблемы. Проблема модификации базисов конечно-элементных аппроксимаций возникла практически одновременно с появлением метода конечных элементов (МКЭ). Однако существенный прогресс в решении задач оптимизации вычислительных качеств КЭ за счет модификации базисов был достигнут лишь в 60-70 -е годы прошлого столетия совместными усилиями инженеров и математиков. Накопленный опыт обнаружил недостатки традиционного матричного подхода к моделированию КЭ, что стимулировало развитие геометрического конструирования базисов. В результате прямого геометрического конструирования были созданы альтернативные модели КЭ, позволяющие корректно формулировать и успешно решать актуальную задачу оптимизации базисов на основе взвешенного усреднения альтернатив.
Анализ предшествующих публикаций, постановка задачи. Первые содержательные результаты, связанные с моделированием и применением четырехугольных КЭ, были получены в 1966 г. (Ergatoudis J.). Настойчивые попытки исключить внутренние узлы лагранжевой интерполяции привели к появлению [1,2] очень полезных, но плохо поддающихся формализации, КЭ серендипова семейства (Irons B., Ergatoudis J., Zienkiewicz O.). Вскоре стало ясно, в особенности, после появления гексагональных КЭ, что возможности матричной алгебры в дискретных аппроксимациях явно недостаточны. В МКЭ стали проникать геометрические приемы построения интерполяционных базисов [3]. Именно благодаря геометрическому моделированию впервые удалось найти альтернативные базисы серендиповых КЭ [4,5]. Было установлено, что альтернативы существуют только на КЭ высших порядков (начиная с третьего). В работе предпринята попытка на примере серендипова КЭ с 12 узлами продемонстрировать возможность управлять формой бикубической поверхности в пределах носителя так, чтобы исключить нарушения в граничных условиях. Это означает, что различные модификации КЭ можно ансамблировать без риска нарушить межэлементную непрерывность.
Цель статьи – показать преимущества геометрического моделирования и протестировать некоторые модификации базисов бикубической интерполяции.
Основная часть. Серендипов КЭ бикубической интерполяции представляет собой квадрат ![]() с 12 регулярно расположенными граничными узлами (рис.1).
с 12 регулярно расположенными граничными узлами (рис.1).
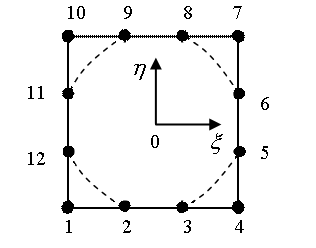
Рис.1 Серендипов КЭ бикубической интерполяции.
Линия нулевого уровня модели с параболоидом вращения.
Из литературных источников [1,2,6] известно, что его единственный базис, найденный подбором, имеет вид:
![]() для угловых узлов
для угловых узлов ![]()
![]()
![]() для
для ![]()
![]()
![]() .
.
![]() для
для ![]()
![]()
![]()
Геометрический анализ приведенного базиса показывает, что бикубические поверхности ![]() состоят из плоскостей и поверхностей 2-го порядка. Наиболее содержательны угловые функции. Они влияют на четыре соседних КЭ, в отличие от промежуточных, влияющих лишь на два КЭ. Естественно, что угловые функции определяют названия моделей. Например, составляющими поверхности
состоят из плоскостей и поверхностей 2-го порядка. Наиболее содержательны угловые функции. Они влияют на четыре соседних КЭ, в отличие от промежуточных, влияющих лишь на два КЭ. Естественно, что угловые функции определяют названия моделей. Например, составляющими поверхности ![]() являются гиперболический параболоид (гипар)
являются гиперболический параболоид (гипар) ![]() и параболоид вращения
и параболоид вращения ![]()
На рис.1 пунктиром показана линия нулевого уровня поверхности ![]() - окружность. Это след пересечения плоскости КЭ с параболоидом вращения. Поэтому приведенная система функций названа моделью с параболоидом вращения (ПВ). Легко заметить, что поверхность
- окружность. Это след пересечения плоскости КЭ с параболоидом вращения. Поэтому приведенная система функций названа моделью с параболоидом вращения (ПВ). Легко заметить, что поверхность ![]() составлена из параболического цилиндра
составлена из параболического цилиндра ![]() и двух плоскостей
и двух плоскостей ![]() и
и ![]() .
.
Примечательно, что возможны и другие композиции. В этом основное преимущество геометрического моделирования. Здесь уместно отметить исключительную роль гипара, без которого не обходится ни одна композиция серендипова семейства.
Можно построить еще одну модель бикубической интерполяции, если в ![]() параболоид вращения заменить параболическим цилиндром
параболоид вращения заменить параболическим цилиндром![]() , который проходит через узлы 2,3,11,12 и точку (-1;-1;1). Образующая параболического цилиндра параллельна диагонали 4-10 КЭ. На рис.2 показаны линии пересечения параболического цилиндра с плоскостью КЭ.
, который проходит через узлы 2,3,11,12 и точку (-1;-1;1). Образующая параболического цилиндра параллельна диагонали 4-10 КЭ. На рис.2 показаны линии пересечения параболического цилиндра с плоскостью КЭ.
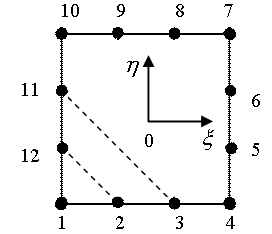
Рис.2 Линии нулевого уровня модели с параболическим цилиндром
Композиция для промежуточных узлов подбирается с учетом интерполяционной гипотезы Лагранжа. Таким образом, модель с параболическим цилиндром (ПЦ) состоит из следующих функций:
![]() ,
, ![]()
![]()
![]() ,
, ![]()
![]()
![]()
Чтобы получить ![]() для остальных промежуточных узлов достаточно в последней формуле переставить
для остальных промежуточных узлов достаточно в последней формуле переставить ![]() и
и ![]() .
.
Сравнение моделей ПВ и ПЦ показывает, что последняя «скрывает» тринадцатый параметр![]() , который в комбинированных моделях способен количественно и качественно изменять аппликаты бикубических поверхностей. Комбинированная модель получается взвешенным усреднением каких-либо двух исходных моделей по формуле
, который в комбинированных моделях способен количественно и качественно изменять аппликаты бикубических поверхностей. Комбинированная модель получается взвешенным усреднением каких-либо двух исходных моделей по формуле
![]()
С помощью весового коэффициента ![]() можно регулировать качество интерполяции. Усреднение, как правило, улучшает качество модели. В математическом моделировании найдется множество примеров, подтверждающих этот тезис. Здесь мы приведем пример модифицированного базиса бикубической интерполяции [7], полученного в результате арифметического
можно регулировать качество интерполяции. Усреднение, как правило, улучшает качество модели. В математическом моделировании найдется множество примеров, подтверждающих этот тезис. Здесь мы приведем пример модифицированного базиса бикубической интерполяции [7], полученного в результате арифметического![]() усреднения моделей ПВ и ПЦ:
усреднения моделей ПВ и ПЦ:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Проведенные исследования [8] подтверждают улучшение качества бикубической интерполяции при арифметическом усреднении ПВ и ПЦ. Интересный результат получен в компьютерных экспериментах [9] при смешивании моделей ПВ и ПЦ в различных пропорциях. Постепенное увеличение доли тринадцатого параметра приводит к сжатию параболоида вращения вдоль диагонали КЭ, содержащей «собственный» узел![]() и одновременному смещению полученного эллиптического параболоида (ЭП) к «собственному» узлу. На рис.3 показана линия нулевого уровня (эллипс) модели ЭП. В диапазоне
и одновременному смещению полученного эллиптического параболоида (ЭП) к «собственному» узлу. На рис.3 показана линия нулевого уровня (эллипс) модели ЭП. В диапазоне ![]() существует бесчисленное множество моделей ЭП, которые мы будем различать по коэффициенту сжатия эллипса в нулевом уровне:
существует бесчисленное множество моделей ЭП, которые мы будем различать по коэффициенту сжатия эллипса в нулевом уровне:![]() , где
, где ![]() - малая ось,
- малая ось,![]() - большая ось эллипса.
- большая ось эллипса.
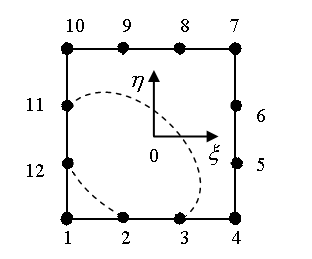
Рис.3 Линия нулевого уровня модели с эллиптическим параболоидом
Вершина эллиптического параболоида находится в точке ![]() . Коэффициент сжатия
. Коэффициент сжатия ![]() . Поэтому данную модель мы обозначили так: ЭП -
. Поэтому данную модель мы обозначили так: ЭП -![]() . Ниже эта модель будет использована в новой комбинации.
. Ниже эта модель будет использована в новой комбинации.
Для создания модифицированных базисов мы используем еще одну модель бикубической интерполяции, которая получена геометрически. Здесь, кроме стандартного гипара, присутствующего в любой «угловой» композиции, используется оригинальный гипар, образующий в нулевом уровне две пересекающиеся прямые (рис.4).
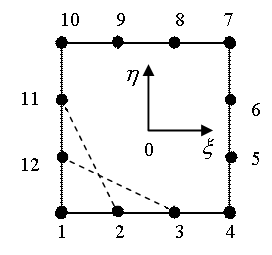
Рис.4 Линии нулевого уровня модели ГП.
Эта модель, названная нами ГП, состоит из следующих функций формы:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Результатом арифметического усреднения модели ПВ и модели ГП явилась модель ЭП-![]() с базисом:
с базисом:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Если же теперь арифметически усреднить модели ЭП - ![]() и ЭП -
и ЭП - ![]() , то получим модель ЭП -
, то получим модель ЭП - ![]() с базисом:
с базисом:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Будем называть ЭП - ![]() - модель 1, ЭП -
- модель 1, ЭП - ![]() - модель 2, ЭП -
- модель 2, ЭП - ![]() - модель 3.
- модель 3.
Модифицированные базисы использованы для построения температурного поля пластины с граничными условиями Дирихле по формуле:
![]()
где ![]() - известные температуры в граничных узлах. Значения температуры в 9 внутренних контрольных точках
- известные температуры в граничных узлах. Значения температуры в 9 внутренних контрольных точках ![]() сопоставляются с точным решением. За точное решение принято решение МКР на сетке с 256 ячейками, полученное методом Гаусса и подтвержденное итерациями Либмана. Для каждой модификации вычисляется среднее квадратичное отклонение от точного решения. Результаты вычислений для двух задач с различными ГУ представлены в таблицах 1-4.
сопоставляются с точным решением. За точное решение принято решение МКР на сетке с 256 ячейками, полученное методом Гаусса и подтвержденное итерациями Либмана. Для каждой модификации вычисляется среднее квадратичное отклонение от точного решения. Результаты вычислений для двух задач с различными ГУ представлены в таблицах 1-4.
Таблица 1
Граничные условия Дирихле для температурного поля пластины
|
|
|
|
|
|
|
|
|
|
Результаты вычислений показаны в таблице 2.
Таблица 2
Сравнение результатов моделирования температурного поля пластины
Точка |
|
|
|
|
|
|
|
|
|
|
Точное решение |
22,715 |
18,217 |
13,103 |
17,705 |
15,999 |
15,258 |
11,014 |
12,871 |
16,917 |
|
Приближенная температура в точке |
|||||||||
|
1 модель |
24,532 |
19,429 |
13,495 |
18,489 |
16,148 |
14,814 |
10,682 |
11,977 |
15,904 |
|
2 модель |
24,3597 |
19,289 |
13,323 |
18,349 |
15,974 |
14,614 |
10,509 |
11,837 |
15,672 |
|
3 модель |
24,446 |
19,359 |
13,409 |
18,419 |
16,061 |
14,714 |
10,596 |
11,907 |
15,788 |
Среднее квадратичное отклонение ![]() ,
, ![]() ,
, ![]() соответственно для 1, 2 и 3 моделей.
соответственно для 1, 2 и 3 моделей.
Таблица 3
Граничные условия Дирихле для температурного поля пластины
|
|
|
|
|
|
|
|
|
|
Результаты вычислений показаны в таблице 4.
Таблица 4
Сравнение результатов моделирования температурного поля пластины
Точка |
|
|
|
|
|
|
|
|
|
|
Точное решение |
8,766 |
9,754 |
6,873 |
11,244 |
11,031 |
8,345 |
15,268 |
14,835 |
12,983 |
|
Приближенная температура в точке |
|||||||||
|
1 модель |
10,159 |
11,092 |
7,775 |
11,876 |
11,254 |
8,127 |
15,003 |
13,906 |
11,723 |
|
2 модель |
9,983 |
10,860 |
7,635 |
11,640 |
10,942 |
7,891 |
14,819 |
13,670 |
11,545 |
|
3 модель |
10,071 |
10,976 |
7,705 |
11,758 |
11,098 |
8,009 |
14,911 |
13,788 |
11,634 |
Среднее квадратичное отклонение ![]() ,
, ![]() ,
, ![]() соответственно для 1, 2 и 3 моделей.
соответственно для 1, 2 и 3 моделей.
Выводы. Наличие альтернативних базисов и принцип взвешенного усреднения открывают широкие возможности для экспериментирования в поисках улучшенных аппроксимаций. Комбинирование бикубических поверхностей чаще всего дает модели с эллиптическим параболоидом (ЭП). Понятно, что качество таких моделей зависит не только от коэффициента сжатия ЭП, но и от граничных условий. Есть предположение, что независимо от ГУ лучшие модели следует искать в небольшой окрестности ![]() . Представляет интерес попытка найти зависимость между коэффициентом сжатия
. Представляет интерес попытка найти зависимость между коэффициентом сжатия ![]() и весовым коэффициентом
и весовым коэффициентом ![]() , по крайней мере, для конкретной пары прототипов.
, по крайней мере, для конкретной пары прототипов.
New models bicubic interpolation are presented. For testing computing properties of model the weighed averaging boundary temperatures on a square plate is used.
1. Зенкевич О. Метод конечных элементов в технике.- М.: Мир, 1975. – 541 с.
2. Норри Д., де Фриз Ж. Введение в метод конечных элементов. – М.: Мир, 1981. – 304 с.
3. Wachspress E.L. A rational finite element basis. – Academic Press. – New York, 1975. – 216 p.
4. Хомченко А.Н. О базисных функциях МКЭ для уравнений в частных производных // III Респ. симпозиум по диффер. и интегр. уравнениям: Тез. докл. – Одесса, 1982. – С.257-258.
5. Хомченко А.Н. О модификации серендиповых элементов /Ив.- Франк. ин-т нефти и газа. – Ивано-Франковск, 1983. – 4 с. Деп. в ВИНИТИ 4.07.83, №3643.
6. Коннор Дж., Бреббиа К. Метод конечных элементов в механике жидкости. – Л.: Судостроение, 1979. – 264 с.
7. Хомченко А.Н., Камаева Л.И. О моделировании конечных элементов серендипова семейства// Прикл. проблемы прочности и пластичности: Всесоюзн. межвуз. сб./ Горький: ГГУ, 1985. – С. 14-17.
8. Манойленко Е.С. Модели конечных элементов для расчетов температурных полей// Сборник научных трудов Херсонского филиала Украинского государственного морского технического университета. Выпуск 1 – Херсон: ХФ УДМТУ, – 2003. – С. 62-68.
9. Козуб Н.А. Модели неклассических серендиповых базисов// Тези доп. IV міжн. н/п конф. «Математичне та прогр. забезпечення інтел. систем. – Дніпропетровськ: ДНУ, 2006. – С. 79-80.
Ответы на вопросы [_Задать вопроос_]
Читайте также
Моделирование объектов и систем управления
Соколов А.Е., Махова Е.О. Моделирование процесса принятия педагогического решения при компьютеризированном обученииСлавко О.Г. Порівняльний аналіз керування регулятором на основі локальної моделі керованого процесу та П-регулятором
Войтенко В.В., Дикусар Е.В, Ситников В.С. Определение частоты среза устройства сглаживания данных на основе метода скользящего среднего
Передерій В.І. Алгоритм визначення та оцінки характеристик ефективності комп’ютерних систем на початковій стадії проектування в умовах невизначенності
Ляшенко С.А, Ляшенко А.С. Оценка модели псевдолинейной регрессии
Ладієва Л.Р. Математична модель процесу газової мембранної дистиляції
Носов П.С., Косенко Ю.І. Нечіткі моделі і методи ідентифікації та прогнозу стану інформаційної моделі студента
Китаев А.В., Глухова В.И. Анализ работы синхронного двигателя с неявнополюсным ротором по данным каталога
Дорошкевич В.К., Пироженко А.В., Хитько А.В., Хорольский П.Г. К определению требований к системам увода космических объектов
Голінко І.М., Ковриго Ю.М., Кубрак А.І. Настройка системи керування за імпульсною характеристикою об’єкта
Яшина К.В., Садовой А.В. Комплексная математическая модель тепловых процессов, происходящих в дуговых электросталеплавильных печах
Шейник С.П., Рудакова А.В. Использование функций принадлежности для моделирования параметров распределенных объектов
Хомченко А.Н., Литвиненко Е.И. Метод барицентрического усреднения граничных потенциалов электростатического поля
Селяков Е. Б. Моделирование требований к техническим системам методами математической логики
Тодорцев Ю.К., Ларіонова О.С., Бундюк А.М. Математична модель контура теплопостачання когенераційної енергетичної установки
Кириллов О.Л. , Якимчук Г.С. Моделирование процесса управления системой перегрузки углеводородных жидких топлив
Шеховцов А.Н., Козел В.Н. Построение математической модели формирования распределенных систем
Китаев А.В., Глухова В.И. Анализ поведения генератора постоянного тока по данным каталога
Хомченко А.Н., Козуб Н.О. Задачі наближення функцій: від лагранжевих до серендипових поліномів
Хобин В.А., Титлова О.А. Определение температуры парожидкостной смеси в дефлегматоре АДХМ по результатам измерений температуры его поверхности
Григорова Т.М., Усов А.В. Вероятностно-статистическое моделирование маршрутизированных пассажиропотоков в крупных городах
Горач О.О., Тернова Т.І. Моделювання технологічного процесу одержання трести при використані штучного зволоження з урахуванням складу мікрофлори
Дубік Р.М., Ладієва Л.Р. Математична модель розділення неоднорідних рідких систем
Казак В.М, Лейва Каналес Родриго, Яковицкая Е.Ю. Моделирование динамики полета магистрального самолета на исследовательском стенде
Завальнюк И.П. Исследование процесса торможения автомобиля как критического режима динамической системы
Дмитриев С.А., Попов А.В. Построение портрета неисправностей проточной части газотурбинного двигателя на примере АИ-25
Русанов С.А., Луняка К.В., Клюєв О.І., Глухов Г.М. Математичне моделювання робочого процесу в апаратах з віброкиплячим шаром та розробка систем автоматизованого моделювання гідродинаміки віброкиплячих шарів
Боярчук В.П., Сыс В.Б. Экспериментальные исследования влияния технологии шлихтования на изменение жесткости текстильных нитей
Селін Ю.М. Використовування контекстних марківських моделей для аналізу дії промислових вибухів на будівельні конструкції
Рудакова А.В. Проблемы интеграции сложных систем
Передерій В.І., Касап А.М. Математична модель та алгоритм автоматизації розрахунку параметрів комп’ютеризованих систем працюючих у реальному часі
Передерий В.И., Еременко А.П. Математические модели и алгоритмы принятия релевантных решений пользователями автоматизированных систем с учетом личностных и внешних факторов на базе генетических алгоритмов
Михайловская Т.В., Михалев А.И., Гуда А.И. Исследование правил клеточных автоматов для моделирования процессов затвердевания квазиравновесных бинарных сплавов
Хомченко А.Н., Колесникова Н.В. Явление «сверхсходимости» в задаче Прандтля для уравнения Пуассона
Китаев А.В., Глухова В.И. Анализ работы трансформатора по данным каталога
Квасницкий В.В., Ермолаев Г.В., Матвиенко М. В., Бугаенко Б.В., Квасницкий В.Ф. Оценка применимости метода компьютерного моделирования к исследованию напряженно-деформиррованного состояния цилиндрических узлов
Китаев А.И., Глухова В.И. Анализ работы асинхронного двигателя по данным каталога
Шелестов А.Ю Имитационная модель взаимодействия GRID-узлов с очередью доступа к общей памяти
Chizhenkova R.A. Mathematical Aspects of Bibliometrical Analysis of Neurophysiological Investigations of Action of Non-ionized Radiation (Medline-Internet)
Хомченко А.Н., Козуб Н.А. Геометрическое моделирование дискретных элементов с криволинейными границами
Славич В.П. Модель автоматизованої системи управління потоками транспортних засобів
Маркута О.В., Мысак В.Ф. Программная реализация и исследование особенностей метода группового учета аргументов
Степанкова Г.А., Баклан І.В. Побудова гібридних моделей на основі прихованих марківських моделей та нейронних мереж
Бакшанська Т.Д., Рижиков Ю.Г., Тодорцев Ю.К. Математична модель процесу горіння природного газу з рециркуляцією продуктів згорання для цілей управління
Хомченко А.Н. Новые решения обобщенной задачи Бюффона
Передерий В.И., Еременко А.П. Математические модели и алгоритмы определения релевантности принимаемых решений с учетом психофункциональных характеристик пользователей при управлении автоматизированными динамическими системами
Ложечников В.Ф., Михайленко В.С., Максименко И.Н. Аналитическая много режимная математическая модель динамики газовоздушного тракта барабанного котла средней мощности
Ковриго Ю.М., Фоменко Б.В., Полищук И.А. Математическое моделирование систем автоматического регулирования с учетом ограничений на управление в пакете Matlab
Исаев Е.А., Наговский Д.А. Математическое описание влияния кривизны контактирующих тел на угол смачивания жидкости в межчастичном пространстве
Бідюк П.І., Литвиненко В.І., Кроптя А.В. Аналіз ефективності функціонування мережі Байєса
Тищенко И.А., Лубяный В.З. Математическое моделирование вокодера для определения оптимальной формы импульса сигнала возбуждения.
Николаенко Ю.И., Моисеенко С.В. Моделирование гармонического полиномиального базиса гексагона.
Клименко А.К. Об упрощенном численном конструировании обратной модели динамического объекта.
Китаев А.В., Сушич Е.Ф. Расчет погрешностей измерительных трансформаторов.
Передерій В.І.,Касап А.М. Математична модель та алгоритм автоматизації розрахунку параметрів комп’ютеризованих систем працюючих у реальному часі
Шпильовий Л.В. Математична модель та алгоритм екстремального управління процесом осадження дисперсної фази суспензії.
Тулученко Г.Я. Інформаційний модуль експрес-пошуку точок еквівалентності процесу нейтралізації.
Тернова Т.І. Урахування морфогенетичного рівняння в математичній моделі тканини.
Попруга А.Г. Теоретические и экспериментальные исследования электрических нагревателей по критерию экономии энергии.
Китаев А.В., Сушич Е.Ф. Приложение положений теории дросселя и трансформатора к расчету и анализу электромагнитом переменного тока.