УДК 519.81:638.51

О НЕКОТОРЫХ ВОПРОСАХ ИДЕНТИФИКАЦИИ ЗНАНИЙ В ИНТЕЛЛЕКТУАЛЬНЫХ СИСТЕМАХ

Булкин В.И., Шаронова Н.В.

Постановка проблемы в общем виде и ее связь с важными научными результатами.  Анализ современных литературных данных свидетельствует, что понятие «знание» определяется в разных источниках по-разному, но большинство авторов соглашаются с тем, что знания имеют ряд особенностей по сравнению с данными. К этим особенностям относятся:

·                    внутренняя интерпретируемость;

·                    структурированность;

·                    связность;

·                    семантическая метрика;

·                    активность.

В настоящее время из существующих моделей представления знаний наиболее популярны логические, сетевые, продукционные, фреймовые модели [2]. В рассматриваемой задаче идентификации знаний в интеллектуальных системах предметной областью обычно называется множество предметов и процессов, которые составляют основу необходимой для решения задачи обработки информации.

Общеизвестно, что языки, предназначенные для описания предметных областей, называются языками представления знаний (ЯПЗ), при этом считается, что универсальным языком представления знаний является естественный язык. Однако использовать его в системах машинного представления знаний сложно, так как он тяжело поддается формализации из-за таких присущих ему явлений, как нерегулярности, полисемия, омонимия, пресуппозиция и т.д. Главным препятствием является отсутствие формализации семантики естественного языка, которая имела бы достаточно эффективную операционную поддержку.

Анализ последних исследований и публикаций, в которых описываются попытки решения подобных задач, показывает, что для представления знаний в информационных системах используются различные формальные языки и, в частности, язык исчисления предикатов. Он имеет однозначную формальную семантику и операционную поддержку в виде совершенного механизма вывода. Кроме того, для описания различных предметных областей предлагается использовать как классические исчисления предикатов, так и различные его модификации, например, многосортное исчисление предикатов первой степени [2].

Постановка задачи. Для представления отношений желательно использовать язык уравнений, т.е. некоторую алгебраическую систему. Преимущество уравнений заключается в том, что с их помощью можно описывать любые отношения на множестве элементов предметной области. Все переменные в уравнении являются равноправными и любые из них могут выступать как в роли независимых, так и в роли зависимых переменных. Алгоритмы и созданные на их основе программы описывают функционирование систем со входами и выходами, а уравнения алгебры описывают функционирование многополюсных систем. В первом случае входы и выходы строго зафиксированы, а во втором случае входные сигналы могут подаваться на любые входы, а выходные сигналы могут сниматься также с любых оставшихся полюсов [3].

В качестве универсального математического языка для описания дискретных, детерминированных и конечных объектов, систем и процессов будем использовать алгебру конечных предикатов [3 – 6], хорошо зарекомендовавшую себя для решения задач обработки текстовой информации.

Любая алгебра представляет собой совокупность множества М с заданными в нем операциями

где А=<M, S>, где М – носитель, а S - сигнатура алгебры [1].

Алгебра предикатов в качестве носителя использует множество U с заданными на нем операциями Ú- дизъюнкции, Ù- конъюнкции и ` - отрицания [5]. В алгебре предикатов используются следующие формулы:

- символы 0 и 1 называются формулами;

- выражения вида  где, ,  называются формулами;

- если выражения А и В – формулы, то выражения (A Ú B ), (A Ù B ) тоже формулы.

Предикатом, заданным на Uⁿ , называется любая функция t = P(x₁, x₂, …, x_n), отображающая множество Uⁿ в множество, где символы 0 и 1 являются логическими булевыми элементами. Элемент 0 имеет логическое значение ложь (False) и может обозначаться латинской буквой F . Элемент 1 имеет логическое значение истина (True) и может быть обозначен латинской буквой Т. Переменные х₁, х₂,…,х_n называются предметными переменными, а их значения называются предметами. Показатель n указывает на степень предиката. Если n = 1, то предикат называется унарным, если n = 2, то бинарным, если n = 3, – тернарным. При произвольном n предикат называют n-арным. Если множество U конечно, то предикат называется конечным, иначе бесконечным.

Дизъюнкцией, или логическим сложением предикатов P  и Q , называется предикат PÚ Q, значения которого при любых xÎ U определяется по формуле

Конъюнкцией, или логическим умножением предикатов P и Q,, называется предикат, значение которого определяется по формуле

Отрицанием предиката Р называется предикат  со значениями, определяемыми в соответствии с формулой

Множество всех n-арных предикатов, заданных над множеством Uⁿ, на котором определены операции дизъюнкция (Ú), конъюнкция (Ù) и отрицание (` ) предикатов, называется алгеброй n-арных предикатов [5]. Операции дизъюнкции, конъюнкции и отрицания являются базисными для алгебры предикатов.

Предикаты вида

называются базисными для алгебры предикатов [4], где а – любой элемент универсума U . Алгебра предикатов полна в том смысле, что любой предикат можно представить в виде суперпозиции базисных операций, примененных к базисным предикатам . Предикат  называется узнаванием (идентификатором) предмета а по переменной х_i . Для алгебры предикатов справедливы тождества:

- закон истинности

- закон ложности

- закон отрицания

Для конечного универсума U = {a₁, a₂, …, a_k} тождества алгебры предикатов можно записать следующим образом:

- закон истинности

- закон ложности

- закон отрицания

С помощью формул алгебры предикатов можно математически описывать любое отношение, заданное на множестве Uⁿ.

Пусть R – отношение на  Uⁿ, тогда предикат Р, значения которого вычисляются по правилу

называется предикатом – идентификатором отношения R. Каждому отношению R соответствует свой предикат Р на  Uⁿ  и наоборот. Каждому предикату Р можно поставить в соответствие отношения R на Uⁿ

Любой предикат Р, заданный на множестве Uⁿ , можно записать с помощью следующей формулы алгебры предикатов:

которая называется совершенной дизъюнктивной нормальной формой предиката Р (СДНФ предиката). При этом ведется логическое суммирование по всем наборам предметов (a₁, a₂, …, a_n), входящим в состав отношения R, которое задается предикатом Р.

Использование алгебры предикатов компенсирует необходимость использования других языков представления знаний (ЯПЗ). При использовании алгебры предикатов объекты и отношения во всех моделях представления знаний записываются в виде уравнений алгебры предикатов. Системы предикатных уравнений могут решаться с помощью универсального решателя, который представляет собой программу, написанную на некотором алгоритмическом языке высокого уровня. Кроме того, любое уравнение алгебры предикатов может быть представлено в виде переключательной цепи, что предоставляет возможность сконструировать процессор представления знаний (ППЗ) из комбинаций таких цепей [4].

Покажем на конкретных примерах, как можно представлять знания, используя алгебру предикатов. В логических моделях для представления знаний широко используются различные виды исчислений предикатов – классическое, многосортное, многоуровневое исчисление предикатов, псевдофизические логики и т.п.

В классическом исчислении предикатов отношение ”z является суммой x и y”, где z, x, y – целые неотрицательные числа (x, y, z Î {0,1, 2, …, n}), записывается в виде предиката

Для нахождения конкретных реализаций этого предиката используется один из языков программирования, например, Пролог. Средствами алгебры предикатов это же отношение может быть задано предикатом

Уравнение

реализует отношение ”число z равно сумме чисел x и y”[4]. Если решить это уравнение относительно переменной z , то получим

Подставляя в это уравнение конкретные значения i, получаем реализацию предиката S(x, y, z)

Если внимательно проанализировать общее уравнение и его конкретные реализации, то обнаруживается, что эти уравнения не только реализуют отношение ”z является суммой x и y”, но и фиксируют знание о том, какие комбинации целых неотрицательных чисел х и у дают в сумме заданное число z.

Любое из вышеприведенных уравнений можно представить в виде переключательной цепи [3], которая представляет собой многополюсник (рис.1), имеющий два входа и один выход. Данная схема представляет собой переключательную цепь, состоящую из 3-х ступеней. На первой ступени расположены схемы узнавания (идентификации) чисел х и у, реализующие базисные предикаты вида t = xⁱ,  t = yⁱ (0 £ i £ n), где t - логическая переменная. Будем называть их предметными идентификаторами (ПИ). На вход этих схем подаются значения чисел х и у, а сигнал 1 формируется на выходе той схемы, которая его идентифицирует (узнает). На выходе остальных идентификаторов формируется сигнал 0. На второй ступени переключательной цепи находится схема совпадения (конъюнкции) на два входа каждая. Количество этих схем совпадает со значением i+1. Третья ступень нашей переключательной цепи реализована схемой разделения (дизъюнкции) и имеет i+1 вход и один выход.

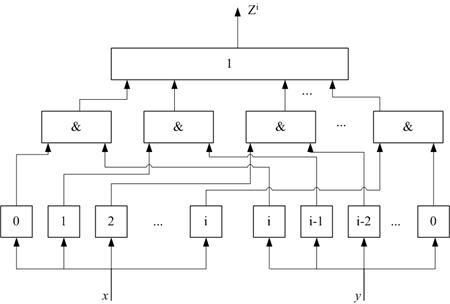
Рис. 1

Схема работает следующим образом. Если на вход многополюсника подаются два числа х и у, то на выходе сигнал 1 появляется только в том случае, если сумма этих чисел равна i. Например, для і = 3 сигнал 1 на выходе схемы будет появляться лишь в том случае, если на вход будут подаваться следующие пары чисел

При подаче на входы переключательной цепи любых других комбинаций (х = 3, у = 1, например) на выходе цепи будет сформирован сигнал 0 .

Рассмотрим теперь пример использования алгебры предикатов для описания предметной области в терминах многосортной логики [2]. В многосортной логике универсум U разбивается на подмножества или, как их называют, сорта, которые отвечают классам сущностей. В отличие от классической логики, кванторы всеобщности и существования ограничиваются областью определения сорта (класса сущностей). Следовательно, прежде чем описывать предметную область, необходимо разбить универсум U на классы эквивалентностей. В многосортной логике это осуществляется простым описанием имен сортов, например, Деталь, Станок, Операция и т. д. На языке алгебры предикатов любое множество U= {a₁, a₂,…,a_n} может быть записано в виде уравнения , где х- предметная переменная, характеризующая данное множество. Совокупность всех корней этого уравнения совпадает с множеством U. Уравнение является формальной записью утверждения х Î U.

На языке алгебры предикатов можно описать любую систему подмножеств М универсума U [4]. Если обозначить имена всех подмножеств некоторого универсума U = {a₁, a₂, ...,a_n} следующими буквами m₀ , m₁ ,…, , то связь подмножеств с их именами может быть задана уравнением вида

где хÎ U, а переменная u (u Î {m₁, m₂,…,m_n-1}) играет роль переменного подмножества универсума U. Любую систему М подмножеств универсума U можно записать, добавив к зависимости (1) уравнение

где j - предикат, задаваемый условиями

Таким образом, любую систему множеств М можно записать уравнением

Например, пусть U = {c, d} . Необходимо описать систему множеств {{ с}, { с ,d }}  .

Систему всех подмножеств U запишем с помощью уравнения  (1)

Уравнение (2) примет вид

Тогда система множеств {{c}, {c,d}} будет записана с помощью уравнения

Используя указанные выше соотношения, можно формально описывать отношения второго порядка, связывающие между собой множества предметов и системы множеств второго порядка, т. е. множества систем множеств предметов. Следовательно, на языке алгебры предикатов можно описывать конструкции многосортной логики. Однако средствами многосортной логики недостаточно адекватно можно описать многоуровневую сложно структурированную предметную область. Для описания структурных зависимостей «класс – подкласс», «часть – целое» между объектами предметной области используется многоуровневая логика. Многоуровневая логика может рассматриваться как расширение многосортной логики за счет введения метода структурирования типов. Отношение «элемент – множество» между объектами А и В записывается (Х/B¹)EQ(A, Х):, Отношение «класс – подкласс» между понятиями В и С – (Х/B²) EQ(C,Х), где EQ – предикат равенства [2].

Данные отношения можно выразить с помощью математических структур высших порядков. Рассмотрим пример математической структуры четвертого порядка. Пусть требуется описать структуру

На языке алгебры предикатов это можно сделать следующим образом. Пусть х – объект некоторой ПрО, u – множество объектов , v – система множеств объектов. Систему множеств v  можно интерпретировать как класс множества объектов, u – как подкласс. Тогда рассматриваемая структура запишется в виде системы уравнений

Здесь символом m₁ обозначен подкласс  {a}, символом m₂ –подкласс {b} , символом m₃-подкласс {a,b}. Символом 1 обозначен класс {{a} , {a,b}}, символом 2 – класс {{b}, {a,b}} [4].

Заключение. Рассмотренные методы идентификации знаний с использованием алгебры предикатов предоставляют возможность единообразного представления знаний в виде уравнений алгебры предикатов. Любое уравнение алгебры предикатов можно реализовать аппаратно в виде переключательной цепи. Используя переключательные цепи, можно конструировать технические средства обработки и хранения знаний в виде некоторого интеллектуального процессора обработки знаний (ИПОЗ).

1.                  Горбатов В.А. Основы дискретной математики: Учебн. Пособие для студентов вузов.- М.: Высш. шк., 1986.-311с.

2.                  Кокорева Л.В., Перевозчикова О.Л., Ющенко Е.Л. Диалоговые системы и представление знаний.

3.                  Шабанов-Кушнаренко Ю.П. Теория интеллекта. Математические средства –Х.: Вища шк. Изд-во при Харьк. ун-те, 1984.-144с.

4.                  Шабанов-Кушнаренко Ю.П. Теория интеллекта. Технические средства –Х.: Вища шк. Изд-во при Харьк. ун-те, 1986.-136с.

5.                  Шабанов-Кушнаренко Ю.П., Шаронова Н.В. Компараторная идентификация лингвистических объектов: Монография.-К.:ІСДО, 1993. –116с.

6.                  Хайрова Н.Ф., Шаронова Н.В. Автоматизированные информационные библиотечные системы: задачи обработки информации: Монографія – Харьков, 2002. – 120 с.