Автоматика.
    Автоматизация.
        Электротехнические
            комплексы и системы.

УДК 004.031.43, 004.93

СРАВНИТЕЛЬНАЯ ЭФФЕКТИВНОСТЬ МЕТОДОВ ПОИСКА В ГЕОМЕТРИЧЕСКОЙ ОБЛАСТИ ДЛЯ ГЕОИНФОРМАЦИОННЫХ КОМПЛЕКСОВ РЕАЛЬНОГО ВРЕМЕНИ

Бородин В. А.

Постановка проблемы. Проблемы поиска в геометрической области широко рассматривались как элементы организации структур баз данных, а также как одно из направлений развития геоинформационных комплексов реального времени (ГК РВ) [1]. В работах [1-6] указывалась важность использования методов поиска в геометрической области при организации вычислительных процедур в ГК РВ.

Актуальность реализации систем ГК РВ, которые бы выполняли такой поиск, а именно, обнаружение всех объектов данного типа в данном участке на земле или в воздухе, подтверждается увеличением количества летательных аппаратов в стратосфере Земли. Сферой применения комплексов с такой функцией может стать наблюдение за спутниками и воздушными объектами из космоса, где приходится обозревать значительные территории, а, следовательно, обрабатывать большие объемы информации о подвижных объектах [4,5].

В системе эта функцию удобно реализовать следующим образом.

У оператора комплекса есть возможность с помощью либо клавиатуры, либо манипулятора компьютера задать область поиска. В реальных задачах эта область должна состоять из сегментов и областей многоугольников. Так оператор задает область поиска и тип объекта поиска. Например, в задачах анализа воздушной обстановки – поиск только самолетов в данной зоне [5].

После составления такого запроса в отдельном окне появляется ответ на запрос. Этот ответ представлен в виде соответствующего списка выявленных объектов, или в виде ответа, что таких объектов не обнаружено. Возможен также вывод соответствующих инструкций в случае обнаружения конфликтных ситуаций. Кроме того, в ряде задач имеет смысл некоторые подзадачи поиска (обнаружение самолета в запретной зоне, обнаружение объектов в опасной близости друг от друга) производить автоматически в фоновом режиме и выдавать сообщение в случае опасности. Такая система повысит вероятность обнаружения системой навигации возможных аварий, что является ключевой задачей ГК РВ для анализа динамической обстановки.

В статье рассматривается задача поиска в прямоугольной области.

Анализ литературы. Данная задача часто возникает для ГК РВ в следующей ситуации. Имеется некоторое изображения участка (или слоя) карты на экране. На фоне этого изображения движутся или просто расположены динамические символы, количество которых очень велико. Для получения возможности рассмотреть и проанализировать обстановку оператор совершает преобразование масштаба – выделяет на экране ту область электронной карты, которую он хочет видеть подробней. Программа отображения картографичечкого фона в ГК РВ осуществляет это преобразование масштаба. После этого программа отображения динамических символов отображает все символы, которые попали в выделенный оператором участок. Для осуществления этой операции комплексу необходимо уметь быстро находить, какие символы и с какими координатами на экране находятся в отмеченном прямоугольнике и осуществить с их координатами соответствующие преобразования, чтобы адекватно отобразить их на фоне нового изображения карты.    

Такой поиск может быть осуществлен путем перебора всех объектов и прямого определения для каждого объекта, принадлежит ли он данной области. Однако, при большом количестве входных данных о движущихся объектах, такие классические структуры баз данных оказываются не удобными в практическом использовании, так как требуют больших затрат ресурсов на отслеживание и обработку изменений [4-8].

Одним из таких методов поиска в прямоугольной области является метод деревьев поиска Бентли [6-8]. Однако такая структура хотя и обеспечивает быстрый поиск в геоинформационных комплексах, часто требует больших затрат времени при быстрых изменениях обстановки [7,9]. 

Для решения этой проблемы каждая запись в базе данных представляется не в виде числа или записи, а в виде функции  от времени, где значение этой функции – вектор пространственных координат или какой-либо другой вектор изменяющихся значений, необходимых по условию поставленной задачи поиска [7].

Рассмотрим методы создания баз данных о таких движущихся объектах в случае, если  - линейная функция.

Пусть  движущихся точек в пространстве  с координатами . Предположим, что мы наблюдаем за точками в дискретные фиксированные моменты времени (периоды обзора). В промежутках между этими моментами времени объекты двигаются по линейному закону . Предполагается, что система может узнавать о законе движения в каждый момент . Такие ограничения вполне естественны для реальных комплексов, поскольку интервалы времени, в которые поступает информация про изменения положений объектов должны быть малы настолько, чтобы эти изменения не меняли картину принципиально. Под этим подразумевается, что в течение времени до следующего обзора не происходило больше одного изменения ответа на запрос.

Возникает следующая задача динамического поиска: Дан прямоугольник  со сторонами, параллельными осям координат и момент времени . Требуется определить  все точки из множества , которые лежат в прямоугольнике  в момент времени , т.е. .

Цель статьи. Целью данной статьи является разработка такой организации программного обеспечения (ПО) ГК РВ, которая бы наиболее быстро осуществляла поиск в геометрической области для анализа динамической обстановки.

Осуществление динамического поиска. Для решения этой задачи используется модель внешней памяти [6,7]. В этой модели предполагается, что каждая операция работы системы предполагает операцию ввода/вывода (I/O operation) массива (блока) длины  данных. Эффективность алгоритма заключается в количестве используемого пространства диска (измеряемого в количестве блоков) и количестве операций ввода/вывода. Такая модель соответствует следующей работе системы: на жестком диске записана база данных об объектах, а операция состоит в том, что компьютер может в течение некоторого момента времени обработать массив длины . Предполагается, что данные хранятся блоками размеров , где - это параметр. Каждая операция с диском предполагает ввод/вывод блока длины .

Через  обозначается функция, которая асимптотически меньше, чем  при  с точностью до константы [6].

Дерево динамического поиска – трехуровневое дерево [7]. Первый уровень – это классическая структура бинарного дерева поиска по - координате, со временем поиска  (первичное дерево).

Этому дереву присваивается вес . Вторичные деревья – это деревья, которые используются для ответа на запрос для плоскости вида . Базовая структура такого дерева – частный случай бинарного дерева, каждая вершина которого  имеет дополнительную структуру , содержащую  точек. Структура  имеет линейный размер, поддерживает поиск в областях вида  и изменяет структуру после добавления новой точки за  и   операций соответственно.

Структура  для ответа на запрос вида состоит из  блоков , хранящих точки и постоянного числа учетных блоков, где -интервал  и -интервал  указывают на каждый блок . Учетные блоки содержат ссылки на эти  -интервалов и - интервалов. Блок  содержит точку с координатами  пока выполняются условия  и .

Блоки строятся следующим образом. Сначала создаются блоки . Для каждого  -интервал  - это интервал  и самая меньшая из  – это . Таким образом  содержит точки . Затем проводится горизонтальная линия и двигается вверх от  и для  подсчитывается количество тех точек, которые лежат над этой линией.

Когда линия достигает точки , такой, что два соседних блока  и  имеют меньше  точек над линией , создается новый блок , в котором  наименьшая точка -интервала и -интервал. Таким образом,  содержит не более  точек  и , которые лежат над линией . Верхние концы отрезков  и  равны  и линия движется для следующего . Так продолжается до тех пор, пока не достигается . Так мы получаем  блоков. Показано [7], что такие блоки строятся за  операций ввода/вывода.

Для ответа на запрос  загружаются в память учетные блоки за  операций. Затем определяются блоки, в которых -интервал включает , т.е. при конструкции которых двигающаяся прямая была вида , и у которых -интервал пересекает . Эти блоки заносятся в память и находятся искомые  точек за  операций.

Эта структура может быть легко динамизирована. Дополнения просто загружаются в дополнительный блок . После того как этот блок заполняется, структура перестраивается за  операций. Таким образом, добавление и удаление новой точки обслуживается за  операцию.

Заметим, что концы интервалов наших структур  определяются 4 координатами  и  и что каждая точка может изменять положение в структуре лишь в фиксированные моменты времени. Эти моменты времени назовем динамическими событиями. В эти моменты и производится динамизация. Для каждой новой точки  мы фиксируем время , когда она покидает . Сохраняем эти значения времени в приоритетном запросе и сортируем по возрастанию, каждое следующее . Дерево для  может быть перестроено за  операций.

Для ответа на запрос  в момент  достаточно загрузить учетные блоки в момент  и выполнять поиск как в предыдущем случае.

Используя похожие идеи можно расширить первичные и вторичные деревья в динамические. События теперь определены в те моменты, когда какие-то из координат точек равны. Эти события могут быть легко обнаружены  за  операций. Структура данных об объектах обновляется тогда за  операций.

Таким образом, если дано множество  из  движущихся точек на плоскости, то существует структура из  блоков, такая, что решение задачи динамического поиска может быть получено за  операций ввода/вывода. Структура данных может быть построена за операций ввода/вывода, в которую можно внести изменения за  операций ввода/вывода.

Пусть дано множество  из  точек  расположенных по возрастанию -координат.

Если необходимо произвести лишь несколько запросов, то не рационально тратить  операций на образование динамического дерева, а достаточно построить структуру данных, которая бы объединяла динамическую структуру с деревьями разбиений [7].

Пусть  - параметр между  и . Конструкция для двигающихся точек на прямой состоит из верхних  уровней динамического разбиения, где , а - по построению ( - некоторая константа,  - количество веток узлов первичного дерева). Дерево имеет  листов. На каждом помещается соответствующее подмножество  точек дерева разбиений.

Каждое динамическое дерево обрабатывает  событий. Таким образом, общее количество динамических операций . Для ответа на вопрос, сколько операций нужно потратить для ответа на запрос нужно сложить количество операций ввода/вывода, необходимых ответа на запрос в дереве с  точками  для всех . Получится  операций, где  некоторое число, большее нуля.

Модифицируем первичную структуру  поменяв все поддеревья уровня , включая их вторичные структуры, динамическими двухмерными деревьями. Для каждого узла  строится вторичная структура . А в  заменяются все поддеревья уровня  динамическими размерности 1 деревьями, где  - глубина  в .

В итоге получается утверждение [7]: Дано множество  из  линейно движущихся точек на плоскости и параметр  из интервала . Тогда можно создать дерево из  блоков, так, что решение задачи поиска может быть получено за операций ввода/вывода. Перестройка БД производятся за  операций ввода/вывода при условии количества изменений в БД ГК РВ  равного  .

Организация поиска в ГК РВ. Описанные методы поиска в геометрической области могут быть реализованы в структуре ПО ГК РВ, которая позволяет обеспечить быстрый поиск при анализе динамической сцены, т.е. произвести определение количества объектов данного типа в выбранном участке пространства, представляемом динамической сценой. Предлагаемая структура базы данных содержит контроллер, который обеспечивает перестройку структуры этой БД либо при поступлении или удалении данных, либо при изменении параметров движущихся объектов как показано на рисунке 1.

Организация программного обеспечения ГК РВ. Предлагается структура программного обеспечения отображения для геоинформационных комплексов реального времени использует три основных класса объектов.

Первую группу составляют карты. Каждая карта представляет собой слои, причем пользователь комплекса может преобразовывать старые и добавлять новые слои. Для каждого из этих слоев реализованы процедуры ОТОБРАЖЕНИЕ (отображение необходимого участка), МАСШТАБ (изменение масштаба), СДВИГ (параллельный перенос), ПОВОРОТ (преобразование данных, обеспечивающее поворот) и ВЫДЕЛЕНИЕ (выделение участка, на котором будет производиться поиск в геометрической области).

Вторая группа  – это динамические объекты (движущиеся цели). Для этих групп объектов реализованы такие процедуры: ОТОБРАЖЕНИЕ-Д (отображение объекта в данной точке экрана), СДВИГ-Д (параллельный перенос данного объекта), ПОВОРОТ-Д (поворот данного объекта на некоторый угол) и функция НАХОЖДЕНИЕ-Д (определяет, находится ли этот объект в выделенной на карте или экране области).

Третей группой является база данных динамических объектов, в которой для выполнения анализа динамической сцены в объекте БД ГК РВ определена процедура ПОИСК, которая и выполняет поиск.

Реализация базы данных ГК РВ представляется следующим образом:

Все динамические объекты хранятся в трехуровневом динамическом дереве, в вершинах которого находятся ссылки на блоки данных поиска , где  выбирается как наибольший массив из записей БД ГК РВ, который может обработать оперативная память компьютера ГК РВ.

Количество операций при осуществлении поиска в прямоугольной области на плоскости (– количество объектов поиска) будет [6-9]: для метода поиска простым перебором – , для метода поиска на основе деревьев Бентли – , для метода динамического поиска – , где  – произвольное положительное число.

Количество операций для перестройки при динамическом  изменении структуры поиска в прямоугольной области на плоскости, т.е. добавления и/или удаления одного объекта будет: для метода поиска перебором – 2, для метода поиска на основе деревьев Бентли – , для метода динамического поиска – .

Таким образом, если количество изменений (перестроек) за время  в базе данных динамического поиска ГК РВ будет , а количество операций поиска, которые надо совершить за то же время будет , то количество операций вообще будет при методе поиска перебором , при методе деревьев Бентли , а при динамическом поиске . Отсюда, метод поиска перебором будет эффективнее динамического поиска при , т.е. 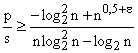, и эффективнее метода деревьев Бентли при . Заметим, что  при . Следовательно, при большом количестве объектов поиска (а именно в этом случае имеет смысл пользоваться нетривиальными методами поиска) пользоваться методом поиска перебором выгоднее при 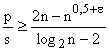. Аналогично, при  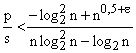поиск с помощью деревьев Бентли будет более быстрым, чем другие методы, а динамический поиск быстрее других методов при  .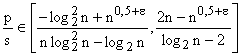

Так, оценивая заранее для данной системы соотношение между  и  можно выбрать наиболее эффективную для данного случая структуру базы динамических данных или в качестве простого нумерованного списка или  в виде трехуровневого динамического дерева.

Выводы. В статье предложен метод быстрого динамического поиска и организация программного обеспечения ГК РВ для отображения и осуществления анализа обстановки в геоинформационных комплексах реального времени.   

В данной  работе представлен сравнительный анализ известных методов поиска в геометрической области применительно к анализу обстановки в ГК РВ. На основании этого анализа утверждается, что при 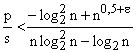 поиск с использованием деревьев Бентли будет более быстрым, чем другие методы, а динамический поиск быстрее других методов 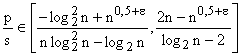при  , при 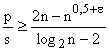 выгоднее же пользоваться методом простого перебора, где  – количество изменений (перестроек) за время работы комплекса в базе данных динамического поиска ГК РВ, а  –  количество операций поиска за то же время.

1.                  Кошкарев А.В., Тикунов B.C. Геоинформатика./Под ред. Д.В. Лисицкого.- М.: Картогеоцентр  «Геодезист», 1993.- 213 с.

2.                  Васюхин М.И., Смолий В.В. Система накопления, обработки и отображения сложных движущихся символов на картографическом фоне // Измерительная и вычислительная техника в технологических процессах.-1999.- № 2.- С.107-110.

3.                  Васюхин М.И. Пути реализации статистических задач анализа воздушной обстановки на основе метода бинарного поиска // Наукові праці Донецького державного технічного університету. Серія “Обчислювальна техніка та автоматизація”.- Вип. 20.- Донецьк: ДонДТУ, 2000.- С.148-158.

4.                  Васюхин М.И. Способы представления данных о движущихся объектах в задачах анализа воздушной обстановки // Наукові праці Донецького державного технічного університету. Серія “Інформатика, кібернетика та обчислювальна техніка”. – Вип. 15. – Донецьк: ДонДТУ, 2000. – С.231-241.

5.                  Беляев А.Г. Использование нетрадиционных логик при определении бесконфликтоности аэронавгиционной ситуации.// Математические машины и системы.- Киев,  2002.- №2..- С.65-74.

6.                  P.K.Agarval. Range searching. //Computing Surveys, 1996, #5, p.1-31

7.                  P.K.Agarval, L.Arge and J.Erickson. Indexing moving points //In Proc.19th Symp on Princeples of Database Systems, p. 175-186, Dallas, Texas, 2000.

8.                  Matousek Juri. Geometric Range Searching.-ACM Computing Surveys, Vol.26., #4, December 1994, р.421-461.

9.                  Васюхин М.И., Бородин В.А. Методы реализации алгоритма поиска объектов в прямоугольной области при анализе воздушной обстановки // Математические машины и системы. - Киев, 2001.- №1-2.- С.100-105.