Автоматика.
    Автоматизация.
        Электротехнические
            комплексы и системы.

УДК 681.3.07                                                                                              

МЕТОДЫ АНАЛИЗА НЕЛИНЕЙНЫХ СИСТЕМ

Сальдо В.В., Шеховцов А.В.

Введение. Очень часто для простоты предполагается, что замк­нутые системы автоматического регулирования представ­ляют собой системы с постоянными параметрами тогда их поведение может быть исследовано с по­мощью линейных дифференциальных уравнений  на базе хорошо разработанной теории линейных следящих систем. Предположение о ли­нейности системы справедливо лишь для весьма огра­ниченного класса систем регулирования [1]. Боль­шинство систем существенно нелинейные и ни для како­го момента времени в них не существует соотношения между входным и выходным сигналами, не зависящего от величины входного сигнала.

Однако нелинейность элементов системы регулиро­вания совсем не обязательно должна вызывать тревогу, так как в ряде случаев наилучшие характеристики си­стемы регулирования могут быть получены именно вве­дением в систему нелинейных элементов.

Постановка задачи. Ниже излагаются  различные подходы к рассмо­трению нелинейных замкнутых систем регулирования, использующих методы, разработанные для линейных си­стем [2].

1. Линеаризация  нелинейных элементов  при  малых отклонениях для получения передаточных функций с по­стоянными  коэффициентами.   Такая  линеаризация   воз­можна при малых отклонениях от рабочей точки, т. е. в тех случаях, когда коэффициенты могут считаться до­статочно постоянными, чтобы быть относительно незави­симыми от амплитуды сигнала, приложенного к входу системы, хотя на самом деле при переходе из одной ра­бочей области  в другую  значения  коэффициентов,  ко­нечно,   меняются.   Этот   метод   линеаризации   позволяет применять линейную теорию к системам регулирования, содержащим нелинейные элементы.  Он в основном ис­пользуется  при  исследовании  устойчивости  систем  при малых отклонениях от начала координат и, кроме того, может применяться для исследования динамики систем при ограниченных значениях задающих и возмущающих воздействий.

2. Линеаризация нелинейных элементов для получе­ния их передаточных функций с помощью метода гармо­нического баланса при больших отклонениях и синусоидальных входных воздействиях. При больших отклоне­ниях от рабочей точки передаточные характеристики являются функциями амплитуды сигнала на входе эле­мента, и в связи с этим для исследования отношения выход - вход необходимо применять разложение Фурье для ряда значений сигнала на входе элемента. Измене­ние характеристик элементов с изменением амплитуды сигнала может служить причиной возникновения неза­тухающих колебаний конечной амплитуды. Исследуя устойчивость таких линеаризованных систем, мы полу­чаем в случае нелинейностей типа «зазор» и «насыще­ние» ответы, близкие к тем, которых мы ожидали на ос­новании нашего практического опыта.

Часто при изучении свойств системы автоматическо­го регулирования представляет интерес исследовать влияние малых изменений величины или величин неза­висимых переменных на выходную величину. В особен­ности это важно при исследовании системы на устойчи­вость, когда необходимо определить, могут ли малые изменения входной величины привести к незатухающим или нарастающим колебаниям выходной величины. Не­смотря на то, что характеристики нелинейных систем для малых вариаций входной величины меняются в за­висимости от рабочей области, для каждого конкретного множества рабочих условий величина выходного сигна­ла приближенно пропорциональна входному сигналу.

Таким образом, в ограниченном смысле для каждого из конкретных условий работы реакцию системы можно положить «пропорциональной входному сигналу» и си­стему, следовательно, «линейной». Поскольку частота и амплитуда нормальных значений входных сигналов, для которых ищется закон управления, обеспечивающий вы­сокую точность, часто таковы, что система находится в «линейной» зоне, важно разобраться в методе опреде­ления линеаризованных характеристик системы в лю­бых требуемых условиях работы.

Здесь следует отметить, что при больших значениях входной величины условия «линейной» работы наруша­ются и эти значения входной величины влекут за собой насыщение основных частей системы управления.

Часто при этих больших значениях входной величины проис­ходит резкий переход из одной рабочей области в дру­гую, и при этом точное регулирование осуществить не­возможно. При плавном переходе из одной рабочей об­ласти в другую предположение о линейности системы в различных точках рабочих областей часто оказыва­ется справедливым.

Принцип малых при­ращений. В качестве од­ного из методов линеари­зации уравнений нелиней­ных элементов систем регулирования использу­ется принцип малых при­ращений. Сначала записываются уравнения, представляющие собой общие соотношения между зависимыми и не­зависимыми переменными. Затем переменные в этих уравнениях переписываются в виде некоторых номиналь­ных значений переменных плюс некоторое приращение, характеризующее отклонение от этого номинального значения. Тогда графические или другие функциональ­ные зависимости между переменными записываются в виде отклонений от номинальных значений, соответ­ствующих номинальным рабочим условиям. И, наконец, в результате получается уравнение или система урав­нений, отражающие соотношения, существующие меж­ду величинами приращений зависимых и независимых переменных.

Анализ задачи. В качестве примера рассмотрим вольтамперную ха­рактеристику. Здесь напря­жение представляет собой независимую переменную, ко­торая вызывает ток, служащий показателем отклонения напряжения от  V. Следовательно,

      I= f (V),                                                                           (1)

где   I - выходной ток,

        V- входное напряжение.

Рассмотрим работу в области напряжения V, кото­рому соответствует ток I. При этом можно записать:

I=I+ ΔI,                                                                        (2)

V=V + ΔV,                                                                     (3)

где ΔI и ΔV представляют собой соответственно прира­щения величины I и V.

Подставив  эти  выражения  в уравнение   (1), по­лучим:

I+ ΔI = ƒ(V + ΔV)                                                      (4)

Разложим уравнение (4) в ряд Тейлора в области точки  (I,V):

I + ΔI = ƒ(V) +                                  (5)

При номинальных рабочих значениях I и  V урав­нение  (1)   может быть переписано в виде:

I = f (V)                                                                     (6)

что, будучи подставлено в уравнение  (5), даст:

ΔI =                                                    (7)

Уравнение (7) указывает на линейную зависи­мость между приращением тока ΔI и приращением на­пряжения ΔV в области  V = V.

Другой иллюстрацией использования принципа ма­лых приращений является часто встречающийся случай, когда регулируемая величина представляет собой про­изведение двух других регулируемых величин.

Рассмо­трим в качестве примера электромагнитный вращающий момент Т, равный произведению потока Ф и тока I. Таким образом,

T = KФI                                                           (8)

Записав каждую переменную в виде суммы номи­нального значения и приращения, получим:

T+ ΔT = K[Ф + ΔФ][I + ΔT]                                           (9)

или

T + ΔT = KФI + KФΔI + KIΔФ,                                 (10)

так как членом второго порядка малости  KΔIΔФ мож­но пренебречь.

Поскольку Т = КФI, уравнение для приращения момента, выраженного через приращения потока и тока, может быть записано следующим образом:

 ΔT = KФΔI + KIΔФ,                                            (11)

Принцип малых приращений часто используется при анализе многочисленных элементов реальных систем ре­гулирования. Характеристики элементов, используемых в системах регулирования тепловых процессов, химиче­ских процессов, аэродинамических процессов, а также электрического и электронного оборудования, часто за­писываются в виде передаточных функций для малых приращений.

Линеаризация нелинейных элементов при больших отклонениях. В этом пункте рассматриваются такие си­стемы регулирования, в которых величина входного сиг­нала влияет на форму переходного процесса в системе. Подход к решению такой проблемы заключается в том, что мы делаем некоторое предположение о диапазоне величин амплитуд сигналов на входе элемента или эле­ментов, обладающих характеристикой, зависящей от ам­плитуды, затем определяем «эффективные» линейные ха­рактеристики этого элемента или элементов и, наконец, определяем частотную или переходную характеристику этой «эквивалентной» линейной системы. В зависимости от характера «линейной» характеристики при одной ам­плитуде сигнала можно определить, каким образом бу­дет меняться амплитуда сигнала и, следовательно, ка­ким будет новое значение эквивалентной «линейной» ха­рактеристики. Следуя этой процедуре итеративным образом, можно приблизиться к установившемуся состоя­нию, в котором амплитуда сигнала в элементе и величи­на сигнала, возвращающегося к этому элементу, согла­сованы. Это установившееся состояние может представ­лять собой устойчивую работу в смысле устойчивой ли­нейной системы или состояние устойчивых автоколеба­ний конечной амплитуды, что является характерным для нелинейных систем.

Эквивалентный комплексный коэффициент усиления для синусоидальных входных сигналов. Основное пред­положение, которое делается при изучении нелинейных систем автоматического регулирования, содержащих эле­менты, испытывающие большие отклонения от линейно­го режима, заключается в том, что если сигнал на входе нелинейного элемента синусоидальный и постоянный по амплитуде, то сигнал на выходе также периодический и той же частоты, что и сигнал на входе. Несмотря на то, что выходной сигнал может содержать некоторое число высших гармоник частоты входного сигнала, предполагается, что частота основной составляющей выходною сигнала та же, что и частота входного сигнала. При этом основная составляющая выходного сигнала связана с входным сигналом через усиление и сдвиг по фазе. Таким образом, для такой амплитуды входного сигнала существует «эквивалентная линейная передаточная функ­ция», для которой амплитуда и фазовый сдвиг выходной реакции по отношению к входному сигналу те же самые, что и для основной гармоники сигнала на выходе нели­нейного элемента по отношению к синусоидальному сиг­налу на его входе. Эта эквивалентная линейная переда­точная функция идентична эквивалентному комплексно­му коэффициенту усиления (описывающей функции), определенной Джонсом [3] как «амплитуда и фазо­вый угол основной составляющей реакции по отношению к предполагаемому входному синусоидальному сигна­лу». Конечно, надо помнить, что эквивалентный ком­плексный коэффициент усиления является функцией ам­плитуды синусоиды на входе нелинейного элемента, так что при определении величины эквивалентного комплекс­ного коэффициента усиления следует указывать ампли­туды входного сигнала.

Сравнение реальной и экви­валентной характеристик некоторого нелинейного эле­мента, где входным сигналом является ко­синусоида с амплитудой I, входной сиг­нал может быть записан следующим образом:

i(t) = ReIe                                                          (12)

Реальный выходной сигнал при входном сигнале та­кого вида является периодическим с тем же периодом, что и период входного сигнала и может быть представ­лен рядом Фурье

O(t) = O                                                         (13)

где O комплексная величина, обладающая модулем и фазой на каждой частоте и задаваемая выражением

O =  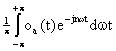                                                       (14)

Эквивалентный   комплексный    коэффициент     усиления этого элемента равен:

G’(a) =                                                                              (15)

где функция а зависит от амплитуды и выражается че­рез   соответствующие   переменные   каждой    конкретной системы. Величина О может быть вычислена с помощью уравнения (15) и представля­ет собой основную со­ставляющую реального выходного сигнала.

При использовании понятия эквивалентно­го комплексного коэф­фициента усиления для решения нелинейных задач делается еще од­но допущение относи­тельно остальной части системы регулирова­ния, кроме основного предположения, кото­рое уже было высказа­но, о том, что частоты входного и выходного сигналов одинаковы. Это второе предполо­жение заключается в том, что в системе име­ются достаточно большие накопители энергии, так что все высокочастотные составляющие выходного сигнала настолько сильно затухают к тому моменту, когда они достигают входа нелинейного элемента, что ими можно пренебречь. Таким образом, условие, что на входе нели­нейного элемента присутствует только синусои­дальный сигнал с частотой основной гармоники, не­смотря на то, что на выходе нелинейного элемента име­ются высшие гармоники, удовлетворяется и высшие гар­моники выходного сигнала можно просто отбросить. К счастью, в большинстве реальных систем регулирова­ния содержатся накопители энергии достаточной емкости, так что необходимое затухание чаще всего обеспечивается. В работах Кохенбургера  и Джонсона [3] рассматриваются специальные примеры, в кото­рых расхождения, вызванные использованием этого ме­тода, не превышают нескольких процентов. Следует от­метить, что метод гармонического баланса дает ответ лишь в первом приближении. В связи с этим часто бы­вает необходимо определить, не приводят ли высшие гармоники к каким-либо затруднениям. Джонсон указал метод, с помощью которого можно получить ответ с бо­лее высокой точностью.

Применение метода гармонического баланса рассма­тривается в следующих примерах, в которых элементы с насыщением и зоной нечувствительности (зазором) описываются с помощью эквивалентных комплексных коэффициентов усиления. Хотя каждый из этих эквива­лентных комплексных коэффициентов усиления получен для номинального значения входного сигнала, равного нулю, в системах может случаться, что синусоидальные колебания происходят не относительно номинального значения, равного нулю, а относительно некоторого сме­щенного значения. В таких случаях выходной сигнал асимметричен и, кроме синусоидальной составляющей, выходной сигнал содержит еще и постоянную составляю­щую. При этом эквивалентный комплексный коэффи­циент усиления является функцией не только амплитуды синусоидального колебания, по и номинального рабоче­го уровня сигнала.

Линейная зависимость между вы­ходным и входным сигналами усилительного устройства механического, электронного, электромагнитного или ги­дравлического справедлива лишь в ограниченном диа­пазоне значений входного сигнала. При входных сигна­лах, больших некоторого предельного значения, выход­ной сигнал перестает увеличиваться пропорционально входному и эффективное отношение выходной сиг­нал/входной сигнал уменьшается. Это явление известно под названием насыщения.

Для упрощения анализа явления насыщения предпо­ложим, что реальная характеристика элемента в инте­ресующей нас области может быть аппроксимирована «идеальной» симметричной характеристикой насыщения, а  +О и -О, где О - значение насыщения выходной величины, приближенно равны значениям вы­ходного сигнала в насыщении при больших положитель­ных и отрицательных значениях входного сигнала. I(предельное значение входного сигнала)  представляет собой значение входного сигнала. Таким образом,

I= .                                                                    (16)

Если на вход усилителя подается сиг­нал вида: i(t) = Isin ωt, где  I> I, то выходной сигнал будет иметь вид для значений i, лежащих в пределах -I< i<I,   выходной сигнал о(t) будет пропорционален i(t)  с коэффициентом пропорциональ­ности K. Для значений i>I  выходной сигнал будет постоянен и равен Определу насыщения О. Анало­гично для значений выходной i<-Iвыходной сигнал будет постоянен и равен О.   Фазовый   угол   α,   при   котором О(t) перестает быть пропорциональным i(t) , равен:

α=arsin(I/I),                                                       (17)

где для такого вида насыщения (I/I) = а. Следует отметить, что значение α  не зависит от частоты входной синусоиды.  

Эквивалентный комплексный коэффициент усиления такого элемента с насыщением  может быть представлен в безразмерной форме в виде отношения к его значению в линейной зоне. Это отношение, или коэффициент изме­нения усиления элемента с насыщением  А, может быть выражено в виде:

A=                                                              (18)

и представлено в виде функции параметра I/I.

Влияние насыщения заклю­чается в уменьшении фактического коэффициента усиле­ния элемента с насыщением. В связи с тем, что предпо­лагалось, что характеристика элемента не обладает  гистерезисом, в выходном сигнале нет сдвига по фазе и единственным результатом насыщения является умень­шение коэффициента усиления.

Заключение. Помимо рассмотренного простейшего «усилительно­го» типа насыщения, главным результатом которого является изменение усиления элемента, влияние насы­щения может проявляться в виде изменения постоянной времени в функции амплитуды сигнала на входе элемен­та. Несмотря на то, что влияние насыщения на постоян­ные времени несколько отлично в том смысле, что ча­стоты, на которых возникает неустойчивость, не могут быть определены так же непосредственно, идея и мате­матический аппарат аналогичны рассмотренным выше.

Зона нечувствительности, или зазор, представляет собой другой тип нелинейности, обычно встречающийся в системах регулирования. Для значений входного сигнала I > I/2 зависимость выходного сигнала  от   входного  линейна   с  коэффициентом   пропорцио­нальности, равным:

K =                                                       (19)

Типичными примерами элементов, обладающих ха­рактеристикой,  являются комбинация датчика с усилителем, а также элемент с механическим зазором.

Если синусоидальный входной сигнал i(t)  с ампли­тудой  подается на вход элемента с зазором, выходной сигнал, как указывалось выше, будет иметь форму i(t)=Isint.  Для +> > -  выходной сигнал равен нулю. Для  ≥выходной сигнал пропорционален величине  - с коэффи­циентом пропорциональности К.

Эквивалентный комплексный коэффициент усиления элемента с зоной нечувствительности может быть выражен в безразмерной форме через свое значение в зоне линейности:

А=                                              (20)

Сравнивая   выражения   (20)   и   (18),   можно заметить, что при одинаковом α справедливо равенство

= 1 - А                                                             (21)   

Так как на величина А отображается в виде функции I/ , то величина  также может быть определена , если вместо I/  воспользоваться уравнением  и использовать уравнение (21).

Уравнение (21) ценно еще тем, что оно подчер­кивает связь насыщения и зо­ны нечувствительности. Для входных сигналов с малой амплитудой (I) влияние насыщения проявляется в незначительном по сравне­нию со случаем отсутствия насыщения уменьшении эк­вивалентного комплексного коэффициента усиления. Напротив влияние зоны нечувствительности для вход­ных сигналов с малой амплитудой заключается в зна­чительном, по сравнению со случаем отсутствия зоны нечувствительности, уменьшении эквивалентного ком­плексного коэффициента усиления. Наоборот, для вход­ных сигналов с большой амплитудой >>I насыще­ние существенно уменьшает эквивалентный комплексный коэффициент усиления по сравнению со случаем отсут­ствия насыщения. И, наконец, влияние зоны нечувстви­тельности в случае входных сигналов большой амплитуды >> проявляется в незначительном измене­нии эквивалентного комплексного коэффициента усиле­ния, по сравнению со случаем отсутствия зоны нечувст­вительности.

1.                  Ямпольский Л. С., Полищук М. Н. Оптимизация технологических процессов в гибких производственных системах. – К.:Техника, 1988.- 175 с.

2.                  Gibson J. E., Non-linear automatic control, New York, McGraw-Hill, 1983.

3.                  Jonson E. C., Sinusoidal analysis of feedback control systems containing non- linear elements, Transactions AIEE, pt. II, vol. 71, p 169-181, 1982.