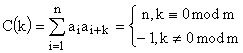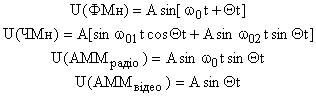Автоматика.
    Автоматизация.
        Электротехнические
            комплексы и системы.

УДК 621.391.1

МАТЕМАТИЧНІ ХАРАКТЕРИСТИКИ ШУМОПОДІБНО КОДОВАНИХ СИГНАЛІВ

Головащенко Н.В.

                В останній час в технічній науці велика увага приділяється розробці та вдосконаленню системам електроніки та зв’зку. Це зобумовлено тим, що при допомозі різноманітних технічних систем і пристроїв вирішуються такі проблеми, як передача інформації, добуття інформації з електромагнітних коливаннь, обробка, зберігання і відображення інформації, передача команд на управляємі об’єкти, контроль і забезпечення функціонування вимірювальних і  виробничих комплексів. В сучасному розвитку науки і техніки інформаційне довкілля постійно змінюється і доповнюється, тому і засоби, які забезпечують і обслуговують це інформаційне довкілля мають постійно розширюватися і вдосконалюватися. Розробки систем зв’язку останнього часу використовують не тільки можливості сучасних технологій, але й найновіші досягнення теорії зв’язку. Вони дозволяють збільшити як об’єми передаваємої інформації, так і якість передачі повідомлень.

             Великий науковий інтерес викликають інформаційні системи, які запроваджуються  для забезпечення функціонування  систем промислового управління і автоматики. Відомо, що в таких системах присутній великий об’єм інформації, яку необхідно якісно і швидко передавати. Для досягнення одночасної передачі великої кількості інформації від різних передавачів використовуються цифрові багатоканальні ситеми передачі данних. [1] Для складних інформаційних систем та для покращення характеристик трактів  прийому-передачі данних використовують складні (шумоподібно кодовані) сигнали. [2]

   Найбільш загальну уяву про властивості сигналу дає автокореляційна функція комплексної амплітуди сигналу:

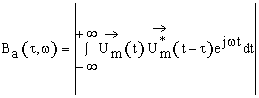,                                          (1)

де  - комплексна амплітуда сигналу,  - комплексно-спряжена амплітуда сигналу, ω,τ – часове і частотне зрушення.

Амплітуда центрального піка автокореляційної функції  прямо-пропорційна тривалості сигналу. Часовий інтервал кореляції зворотньо-пропорційний смузі частот сигналу. Таким чином,  дає змогу говорити про потенційну завадостійкість і розподільчу здатність за часом, що забезпечуються сигналом. У випадку, якщо взаємокореляційні функції сигналів , тобто, не мають яскраво виражених піків, а невеликі викиди розподілені по вісі часу, то  є еквівалентом ортогональності сигналів. Для ортогональних сигналів  та  має виконуватися умова:

Тобто, осереднений добуток двох сигналів  та  дорівнює нулю. Така властивість сигналів необхідна при побудові багатоканальних систем передачі інформації. Таким чином, функції  та  дозволяють вирішувати питання про перспективність сигналів для створення багатоканальних систем приймання-передачі.

До класу складних сигналів відносять шумоподібні сигнали.  В сигналі присутня введена надмірність кода, і тому база складного шумоподібного сигнала буде набагато більшою за одиницю:

де  - смуга частот сигнала,  - тривалість сигнала.

Базу сигнала можливо збільшити за рахунок збільшення  , при цьому збільшиться енергія сигнала і як наслядок цього підвищиться завадостійкість прийома-передачі інформації. А ще можливо збільшити базу за рахунок збільшення  , при цьому збільшується розподільна здатність за часом, яка важлива при розробці пристроїв синхронізації.

Автокореляційна функція шумоподібних сигналів (АКФ) подібна АКФ шуму. І, у той же час, вони синтезуються за законами цілком детермінованих функцій – двійкових квазівипадкових послідовностей (КВП), які називають послідовностями еквівалентними імпульсу. Детеміновані послідовності, що мають властивості послідовностей, елементи яких вибираються випадково, називають квазівипадковими. АКФ цих послідовностей має один вузький з великою амплітудою центральний пік і значно менші по амплітуді бічні викиди. АКФ шумоподібних сигналів подібна АКФ КВП.

Застосування КВП як модулюючих функцій забезпечує простоту апаратурних рішень у випадках розширення смуги частот сигналу і збільшення загальної тривалості сигналу.

Структурна  схема системи прийому-передачі інформації з використанням шумоподібно кодованих сигналів приведена на малюнку 1.

Вих.

Рис. 1 Структурна схема системи прийому-передачі інформації з використанням шумоподібно кодованих сигналів.

Основними апаратурними частинами прийомо-передаючої системи, які дозволяють відтворити переваги шумоподібних сигналів є генератор квазівипадкових послідовностей і цифровий корелятор. Генератор квазівипадкових послідовностей визначає структуру шумоподібно кодованого сигналу, а цифровий корелятор здійснює узгоджений за структурою сигнала прийом.

Генератори КВП прості в апаратурному виконанні. Можна сказати, що генератори ШКС не викликають утруднень при апаратурній реалізації, а самі ШКС мають гарні потенційні можливості для удосконалення трактів приймання-передачі.

Серед двоїчних квазівипадкових послідовностей найбільш відомі m – послідовності, це послідовності максимальної довжини.

Усі КВП можна розділити на три групи: лінійні, нелінійні, кодові слова. Лінійні – процес, використаний при її генерації, лінійний. Лінійність обумовлена тим, що до цього процесу можна застосувати принцип суперпозиції. Для нелінійної зостосовуються два методи утворення:

1)      використання нелінійної логіки при генеруванні;

2)      застосування нелінійної вихідної матриці разом з лінійним генератором.

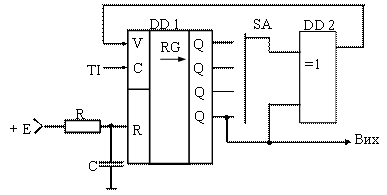
Рис. 2 Канонічна структурна схема генератора КВП

На малюнку 2 зображена канонічна функціональна схема генератора лінійних КВП. Складається вона з регістра зрушення і суматора по модулю 2, включеного в ланцюзі зворотного зв’язку генератора. Період і структура КВП визначаються місцем включення зворотного зв’язку. DD1 – регістр зрушення, у даному випадку чотирирозрядний, тобто, n=4 і максимальна довжина періоду m=2ⁿ-1=15. DD2 – суматор по модулю 2. SA – комутатор. Він визначає структуру КВП.

Лінійним КВП максимальної довжини притаманні  такі основні властивості, що визначаються властивостями чисто випадкових двоїчних послідовностей:

1)      число “одиниць” за період завжди на одну більше числа “нулів”;

2)      періодична АКФ дорівнює

де =1 чи 0, m – довжина максимальної послідовності.

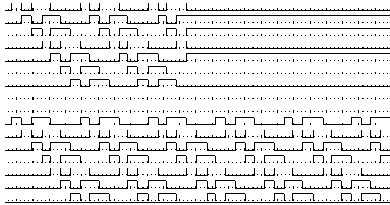
            Часові діаграми, які пояснюють принцип створювання ШКС зображені на рис. 3. Їх структура відображує структуру квазівипадкових послідовностей.

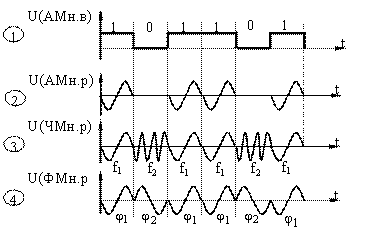
Рис. 3 Часові діаграми шумоподібно кодованих сигналів

В даному випадку:

де  - довжина елементарного кодового знака, Т – довжина послідовностей.

Принцип формування полягає в тому, що “одиниці” коду повинні відповідати одній амплітуді (частоті, фазі), а “нулі” коду – іншій амплітуді (частоті, фазі). Таким чином можна сформулювати амплітудно-маніпульовані відеосигнали (АМн-відео, часова доріжка 1), амплітудно-маніпульовані радіосигнали (АМн-радіо, часова доріжка 2), частотно-маніпульовані радіосигнали (ЧМн-радіо, часова доріжка 3), фазоманіпульовані радіосигнали (ФМн-радіо, часова доріжка 4). Алгоритми формування можна описати таким чином:

Згідно з рис. 3 математичні моделі зображених ШКС можна записати таким чином:

де        А – амплітуда сигналу;

ω₀, ω₀₁, ω₀₂, - частоти,

.

Структурна модель генератора ШКС зображена на рис. 4, де прийняті наступні позначення:

G₁ [] - генератор сигналів з першою амплітудою, частотою, чи фазою; G₂ [] - генератор сигналів з другою амплітудою, частотою, чи фазою; К₁ і К₂ – перемикаючі пристрої; R1; R2; R3 – пасивний суматор (на резисторах).

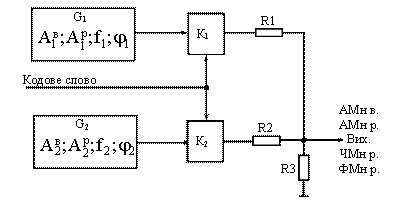
Рис. 4 Структурна схема генератора ШКС

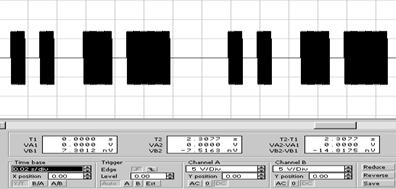
а)

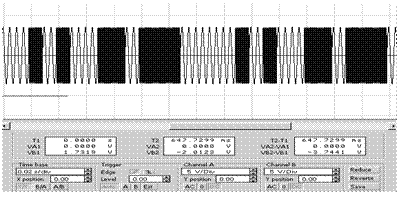
б)

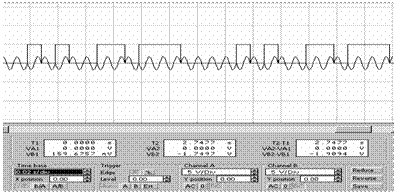
в)

Рис. 5 Часові діаграми сигналів генератора ШКС

а) амплітудно-маніпульований сигнал; б) частотно-маніпульований сигнал;

в) фазо-маніпульований сигнал.

Для передачі сполучень використовується деякий набір /множина/ сигналів. На функціонування линиї зв’язку суттєво впливають кореляційні характеристики цих сигналів.[4]

Нехай використовується набір сигналів {S_i}={S₁, S₂,…,S_M}, де  i = 1, 2, …, M.

Автокореляційна функція сигнала буде мати вигляд:

                                                  (8)

Взаємокореляційна функція сигналів:

                                                  (9)

Риска над символом означає статичне осереднення, тому такі кореляційні функції називаються статичними. В загальному випадку функції  залежать від двох аргументів: часу t, та відносного часового зсуву τ. Існує клас процесів, для яких кореляційні функції не залежать від часу. Процеси, для яких автокореляційна функція  не залежить від часу, називаються стаціонарними в широкому розумінні. Для таких процесів =. Якщо для функцій   та  взаємокореляційна функція не залежить від часу, то такі функції називаються стаціонарно-пов’язаними у широкому розумінні. Для них справедливе рівняння:

=.                                                                          (10)

Кореляційні функції наборів сигналів  утворюють прямокутну кореляційну матрицю  розмірністю М*М, по головній діагоналі якої розташовані автокореляційні функції (М – число сигналів у наборі).

Часова періодична взаємокореляційна функція періодичних сигналів   та  має вигляд :

                                                    (11)

Для ергодичних процесів:

;                                                       

                                      (12)

Два сигнали   та  називаються ортогональними, якщо виконується співвідношення:

                                             (13)

Широко застосовується поняття коефіцієнта автокореляції, обумовленого рівнянням:

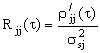                                                            (14)

 де  - дисперсія сигналу .

Коефіцієнт взаємної кореляції:

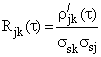                                                        (15)

 де  - діючі значення сигналів  та .

Максимальне значення коефіцієнта кореляції ± 1.

Якщо коефіцієнт взаємної кореляції дорівнює нулю при всіх τ, то функції   та  називаються некорельованими. Поряд зі звичайними кореляційними функціями  широко використовують знакові кореляційні функції. Їх розрахунок потребує менших затрат. Технічні спрощення при автоматичному розрахунку знакових кореляційних функцій досягаються завдяки тому, що процеси які досліджуються (один або обидва з кожної порівнюваної пари процесів) замінюють їх знаками /полярностями/. З цією метою використовується функція Sgn x – сігнум (знак) х, яка обумовлена рівнянням:

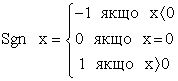                                           (16)

Знакова взаємна кореляційна функція  стаціонарно пов’язаних випадкових процесів X(t) та Y(t) обумовлена рівнянням:

                                     (17)

 Припустив, що X=Y будемо мати вираз, для знакової автокореляційної функції  стаціонарного випадкового процесу:

                                         (18)

 Знакові кореляційні функції лінійно пов’язані з імовірностями збігу знаків /полярностей/

                                           (19)

 де ; Р  - символ імовірності.

Виходить, що в деяких випадках апаратурне визначення знакових кореляційних функцій зводиться до визначення імовірностей збігу знаків.

            Для квазіоптимального прийому в приймачі доцільно використовувати  знаковий цифровий корелятор[5], структура якого зображена на малюнку 6.

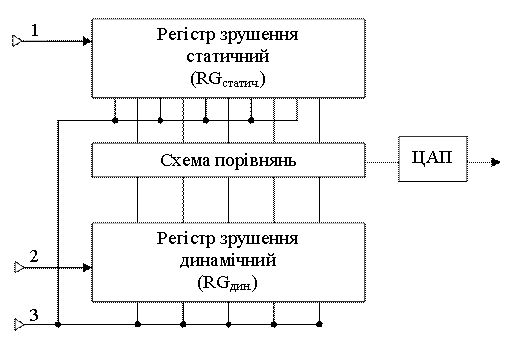
Рис.6 Структурна схема знакового цифрового корелятора

Принцип роботи цифрового корелятора полягає в тому, що на вхід статичного регістру зрушення для запису в пам’ять та в лінію зв’зку подається  кодове слово. На вхід  динамічного регістру зрушення подається кодове слово, яке вже пройшло лінію зв’зку та пристрій відновлення його структури. Схема порівнянь визначає кількість порозрядних збігів кодових слів з статичного і динамічного регістрів. Таким чином цифровий корелятор визначатиме ступінь відповідності між прийнятим кодовим словом і тим, що знаходиться у пам’яті корелятора. При моделюванні ціфрового корелятора за допомогою прикладної програми Electronics Workbench була отримана автокореляційна функція  ШКС, та можливо наочно побачити зберігання КСП в статичному регистрі зсуву (малюнки 7 та 8 відповідно).

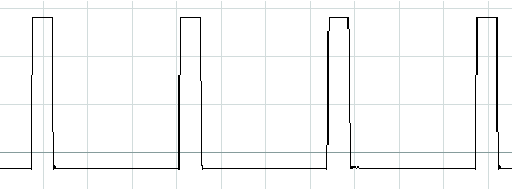
Рис.7 Автокореляційна функція ШКС

Рис.8 Зберігання КСП в статичному регистрі зсуву

Таким чином, з огляду математичних характеристик шумоподібно кодованих сигналів, необхідно відмітити переваги використання цих сигналів в інформаційних системах:

-                     можливість прийому та обробки сигналів при відношенні сигнал/перешода багато меньших одиниці;

-                     висока завадостійкість як по відношенню до широкосмугових, так і до вузькосмугових перешкод;

-                     існує перспективність  шумоподібно кодованих сигналів для створення багатоканальних систем приймання-передачі;

-                     висока вірогідність інформації, яку приймаємо.

1.                  Баева Н.Н. Многоканальная электросвязь и РРЛ: Учебник для вузов. - М.: Радио и связь, 1988. – 312с.: ил.

2.                  Корниловская  Н.В. Применение шумоподобных кодированных сигналов в системах промышленной автоматики. – ААЭКС №1 Херсон – 2001. – с.29-37.

3.                   Методичні вказівки для виконання лабораторних робіт з дисціпліни “Цифрова електроніка та ЕОМ в системах управління” для магістрів спеціальності 8.091.401 “Системи управління і автоматики”. /Корніловський В.П., Корніловська Н.В., Головащенко Н.В.-Херсон, ХДТУ, 2003, - 19 с.,Укр.мовою.

4.                   Нефедов В.И. Основы радиоэлектроники и связи: Учебник для вузов/ В.И. Нефедов – 2-е изд., перераб. и доп. – М.: Высш. шк., 2002. – 510 с.: ил.

5.                   Головащенко Н.В., Боярчук В.П.  Аппаратурный состав для улучшения свойств трактов приёма-передачи информации в системах промышленной автоматики. – ААЭКС № 1 (11) Херсон – 2003.  – с.58-61