Автоматика.
    Автоматизация.
        Электротехнические
            комплексы и системы.

УДК 519.7

О  ВЛИЯНИИ  КОНСТРУКТИВНЫХ  ПАРАМЕТРОВ  ОБРАТНОЙ  МОДЕЛИ НА  ЕЁ  УСТОЙЧИВОСТЬ

Клименко А.К.

1. Постановка проблемы и её связь с практическими заданиями

Последние годы характеризуются бурным развитием компьютерных информационных технологий. Использование аналитических преобразований совместно с численными методами даёт возможность создавать новые подходы для решения задач в различных областях науки и техники.

 Для решения многих задач управления и контроля требуется применение обратной модели (ОМ) динамического объекта (ДО). Идеальная ОМ реального объекта, как известно [1], неосуществима. На аналоговых средствах техники удавалось создавать лишь приближенные ОМ для ДО, описываемых уравнениями не выше второго порядка. Применение средств вычислительной техники позволило найти технические решения ОМ [2,3], приближающие её показатели качества к идеальным и не зависящие от порядка описываемых ДО уравнений. Кроме того, на этих средствах удалось разработать и ОМ для многосвязного ДО [4].

 При создании дискретной ОМ возникают две проблемы.

 Первой из них является определение пределов изменения конструктивных параметров ОМ, в которых обеспечивается её устойчивость, а второй — уточнение этих параметров для получения желаемых показателей качества.

 При создании дискретной обратной модели обе эти проблемы решаются путём нахождения двух конструктивных параметров – дискретности времени Т и временного сдвига τ. Уменьшение этих параметров дает возможность приближать показатели качества создаваемой модели к идеальной, но сопровождается повышением колебательности ОМ вплоть до потери устойчивости.

 В техническом решении ОМ, приведенном в работах [2,3], не возникает проблемы обеспечения устойчивости в случае, когда ДО описываетя уравнением первого порядка. Повышение порядка уравнения приводит к проблеме как устойчивости, так и показателей качества. В ОМ [5] удаётся подавить колебательность, но проблема обеспечения устойчивости сохраняется. В работе [6] предлагается техническое решение ОМ, обеспечивающее возможность улучшать её показатели качества за счёт одновременного уменьшения параметров Т и τ. Устойчивость в этом случае может быть обеспечена при определенном соотношении между этими параметрами.

 В данной работе рассматривается проблема определения области устойчивости создаваемой ОМ в функции двух конструктивных параметров: дискретности времени Т и временного сдвига τ.

 Проблема рассматривается на примере ОМ [6] с получением выводов о применимости полученных результатов к другим техническим решениям её.

2. Анализ известных решений и применение их к исследованию устойчивости ОМ

  Каждая из ОМ, рассматриваемых в данной работе, является замкнутой импульсной системой без непрерывной части. В её математическом описании нет алгебраического характеристического уравнения, поэтому для исследования её на устойчивость целесообразно обращаться к критерию Найквиста. Для этого прежде всего нужно найти математическое выражение частотной характеристики ОМ в разомкнутом состоянии.

 Обратная модель создаётся для линейного стационарного динамического объекта (ДО), который устойчив и функционирует в непрерывном времени. В качестве математического описания ДО может выступать его передаточная функция W(s) или переходная характеристика h(t). Дальше в качестве математического описания ДО будем рассматривать его переходную характеристику (кривую переходного процесса). Последняя может быть получена как обратное преобразование Карсона-Хевисайда от его передаточной функции или найдена экспериментальным путём. Полагаем, что переходный процесс равен нулю в начальный момент времени и устанавливается на конечном интервале Т₂, т.е.

 , ,                                                    (1)

где — установившееся значение переходного процесса.

 Переходная характеристика может быть представлена в дискретном времени:

                     (2)

где T — шаг квантования (дискретность времени),

 γ — дробная часть дискретного времени,

 N₂ — время затухания переходного процесса .

 n — дискретное время ( , где - моменты непрерывного времени, кратные ).

 В качестве математического описания ДО при конструировании ОМ используется числовой массив его импульсной переходной функции (ИПФ), который может быть получен из переходной характеристики (2) в дискретном времени:

                  (3)

 При разработке ОМ задаются численные значения дискретности времени Т и временного сдвига  в выражениях (2) и (3).

 Математическое описание приведенной в [3] ОМ имеет вид:

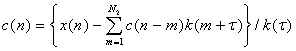 ,                  (4)

где x(n) и c(n) – соответственно входной и выходной сигналы ОМ,

  – переменная суммирования,

 t – конструктивный временной сдвиг, удовлетворяющий условиям:

                                    (5)

 На основании приведенных в [3] материалов можно показать, что описываемая уравнением (4) ОМ устойчива по Найквисту, если на комплексной плоскости точку с координатами -1,j0 не охватывает частотный годограф

 , ,      (6)

где  - приведенная к дискретному времени частота ().

 Приведенные выше зависимости (1-6) предназначены для использования при решении задач данной работы.

3. Постановка задач

 Сформулированное выше условие устойчивости относится к техническому решению ОМ, приведенному в работе [3]. Оно не дает сведений о конкретном влиянии конструктивных параметров T и τ на устойчивость. Кроме того, нет сведений о возможности использования этого условия при исследовании на устойчивость ОМ по работе [6].

 Задачами данной работы являются:

 - нахождение условия устойчивости ОМ по техническому решению [6],

 - определение границы устойчивости обратных моделей на плоскости параметров T и τ независимо от их технического выполнения.

4. Изложение материалов исследования

 Известная из [6] ОМ описывается математической зависимостью

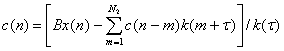 ,                     (7)

где B – постоянный коэффициент, определяемый в процессе моделирования.

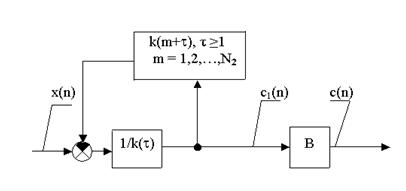
Рис.1 Структурная схема обратной модели

 Эта ОМ может быть представлена как импульсная следящая система с изображённой на рис.1 структурной схемой. Звено с коэффициентом передачи B находится вне замкнутого контура и на устойчивость не влияет. Замкнутый же контур описывается уравнением (4), а его частотная характеристика в разомкнутом состоянии имеет вид (6).

 Отсюда следует, что условия устойчивости у технических решений ОМ по [3] и [6] идентичны.

 Для определения границы устойчивости ОМ на плоскости параметров T и τ поступаем следующим образом.

 Как известно [7], частотная характеристика разомкнутой импульсной системы симметрична относительно действительной оси и пересекает её при относительной частоте . Полагаем, что разомкнутый контур устойчив и его частотный годограф не пересекает действительной оси при . Тогда необходимым и достаточным условием устойчивости замкнутого контура будет выполнение неравенства:

                                           (8)

 Подставляем в неравенство (8) выражение для  из (6) и решаем его, принимая во внимание, что , а . В результате решения получаем условие устойчивости:

 .                                         (9)

 Обозначим правую часть неравенства (9) символом и назовём её остаточной суммой знакопеременного ряда чисел ИПФ ДО. Сам же числовой массив  получен из математического описания ДО при выбранных параметрах T и τ ОМ с использованием зависимостей (3) и (5).

 Условие устойчивости (9) словесно можно сформулировать так: численные значения дискретности времени T и конструктивного временного сдвига τ ОМ должны выбираться таким образом, чтобы первый член числового ряда ИПФ ДО  был больше остаточной суммы .

 Переменные  и являются функциями конструктивных параметров ОМ:  и . На рис.2 в качестве примера приведены графики зависимостей  и  от величины дискретности при постоянном значении τ. При весьма малой дискретности имеет место  < , что свидетельствует о неустойчивости ОМ. При росте дискретности остаточная сумма сначала увеличивается вместе с , а затем быстро уменьшается. При определённом значении дискретности = Т^* справедливо равенство =, что свидетельствует о границе устойчивости.

 В случае изменения параметра τ изменится и значение дискретности Т^*, соответствующее границе устойчивости. Поэтому возникает потребность построить кривую границы устойчивости в плоскости параметров T и τ. Границе устойчивости соответствует преобразование неравенства (9) в равенство. Перенеся сумму из правой

части неравенства в левую и заменив знак неравенства на знак равенства, получим уравнение для построения кривой границы устойчивости:

.

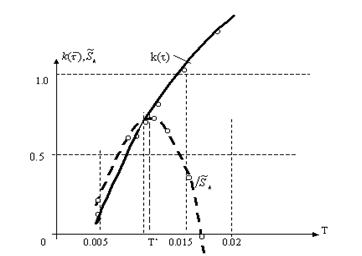
Рис.2 Графики зависимостей и  от дискретности T

 Левая часть полученного уравнения представляет собой полную сумму знакопеременного ряда из числового массива ИПФ ДО. Она является функцией двух переменных. Обозначим её символом

 Уравнение границы устойчивости получает вид:

 0.                                                 (10)

5. Экспериментальная часть

 Порядок построения кривой границы устойчивости на плоскости параметров T и τ для проверки полученных теоретических результатов состоит в следующем.

 1. Задаются исходные данные о ДО, для которого создается ОМ. Таковыми является математическое описание кривой переходного процесса h(t) в непрерывном времени.

 2. Задаются первые приближенные значения конструктивных параметров T и τ. Например, =1, а дискретность  принимается равной одной десятой от времени затухания переходного процесса T₂.

 3. Вычисляется числовой массив h(n) по формуле (2), учитывая, что γ = τ.

 4. Вычисляется числовой массив k(n+τ) по формуле (3).

 5. Вычисляется полная сумма знакопеременного ряда и проверяется соответствие полученного значения уравнению (10).

 6. Если 0, то при заданных параметрах и  ОМ находится на границе устойчивости. Это можно отметить постановкой точки на плоскости параметров и перейти к п.2, задав новое значение .

 7. Если  > 0, что свидетельствует об устойчивости ОМ, вернуться к п.2, уменьшить ранее заданную величину  и повторить операции по пунктам 3-5. В случае, если  < 0 , сделать то же самое, но при увеличении .

 По полученным данным строится кривая границы устойчивости.

 Пример такой кривой приведен на рис.3. Находящаяся ниже полученной кривой область параметров 1, отмеченная штриховкой, является областью неустойчивости.

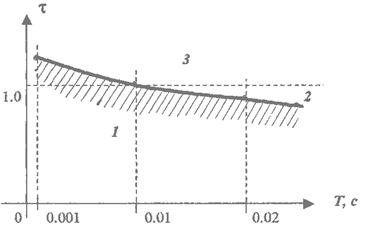
Рис.3 Граница устойчивости на плоскости параметров T и τ

 Полученные результаты подтверждены моделированием. При этом были использованы как специально разработанные программы, так и пакет прикладных программ MathCad.

6. Выводы по результатам исследования и перспективы

 Наличие графика границы устойчивости на плоскости параметров облегчает разработку обратной модели для данного ДО. Сам график может выступать как составная часть математического описания ДО.

 Процесс конструирования ОМ сводится к выполнению следующих операций.

 Из исходного математического описания ДО строится кривая переходного процесса и устанавливается время его угасания. Определяются первоначальные значения параметров  и , Вычисляются числовые массивы h(n) и k(n).

 Строится кривая границы устойчивости (10).

 По кривой границы устойчивости выбирается техническое решение ОМ.

 Выбор совокупности значений T и τ в области 1 по рис.3 неприемлем, т.к. не обеспечивает устойчивости ОМ. Если желаемые параметры находятся в области 2 , то может быть использовано техническое решение ОМ из [3] или [5]. При нахождении совокупности конструктивных параметров ОМ в области 3 выбирается техническое решение [6].

 Полученные результаты создают предпосылки для разработки методики численного конструирования ОМ с получением желаемых показателей качества. Работа в этом направлении ведётся.

 Изложенные результаты могут быть использованы и в инженерно-педагогических учебных пособиях для освоения новых способов решения задач на основе современных компьютерных технологий.

1.                   Петров Б.Н., Кухтенко А.И. Теория проектирования инвариантных систем. Современные методы проектирования систем автоматического  управления / Под ред. Б.Н. Петрова, В.В. Солодовникова, Ю.И. Топчеева. – М.: Машиностроение, 1967. – С. 18 – 78.

2.                   Клименко А.К., Клименко  В.Г.  Корректирующее устройство. А.с.  1406563 (СССР).

3.                   Клименко А.К. Обратная динамическая модель для решения задач управления и контроля качества // Методы менеджмента качества . – 1999. - № 8. – С. 32 – 39.

4.                   Клименко А.К. Обратная  модель  для  контроля  качества  многосвязных динамических объектов // Методы менеджмента качества. – 2000. - № 5. – С. 36-40.

5.                   Клименко А.К. О подавлении колебаний в дискретной обратной  модели // Надёжность и качество 2002: Труды международного симпозиума  /Под ред. Н.К.Юркова.— Пенза : Информационно-издательский центр Пенз. гос. ун-та, 2002.  – С. 138-139.

6.                   Клименко А.К. Обратная модель с улучшенными показателями качества // Надёжность и качество 2003: Труды международного симпозиума  /Под ред. Н.К.Юркова.— Пенза : Информационно-издательский центр Пенз. гос. ун-та, 2003.  –  С.237-239.

7.                   Цыпкин Я.З.  Теория линейных импульсных систем. – М.: Физматгиз, 1963. – С.269.