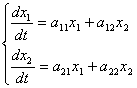УДК 681.516.4: 681.5.037
ИССЛЕДОВАНИЕ КРИТИЧЕСКИХ РЕЖИМОВ АВТОКОЛЕБАТЕЛЬНЫХ СИСТЕМ
Завальнюк И.П., Бражник А.М.
Введение. Важную группу динамических систем представляют системы, в которых возможны колебания. Большинство реальных колебательных систем в различных областях техники неконсервативны (с изменяющимся во времени запасом энергии). Среди них выделяется особый класс так называемых автоколебательных систем, преобразующих энергию источника в энергию незатухающих колебаний, причем основные характеристики незатухающих колебаний (амплитуда, частота, форма колебаний и т.д.) определяются параметрами системы и в некоторых пределах не зависят от выбора исходного начального состояния. Энергия представляет собой не только основной инвариант динамической системы, но и является мерой взаимодействия различных систем. По своему физическому смыслу внутренняя энергия системы является мерой ее возможности совершения работы. Задача изменения энергии за счет внешних воздействий (управлений) может иметь как теоретическое, так и практическое значение. Например, для энергосберегающих технологий важной задачей является преобразование энергии системы без неоправданных потерь энергии внешних воздействий.
Работа той или иной системы сопровождается потерей устойчивости одними режимами её функционирования и рождением новых, устойчивых. Изменения могут накапливаться плавно, а могут происходить скачком в виде катастроф [1-3]. При потере устойчивости предшествующего режима система выбирает новый устойчивый режим, который может наследовать некоторые свойства предыдущего, а может быть и резко отличным.
Постановка задачи. Большой интерес представляет исследование поведения динамических систем при переходе в критический режим функционирования, а также при изменении функции диссипации.
Анализ последних исследований и
публикаций. Для объяснения физической
природы автоколебаний в [4] рассмотрен энергетический баланс колебаний. Отмечено, что наряду с формами
энергии, используемыми для объяснения собственных колебаний (потенциальной и
кинетической энергий) в автоколебаниях определенную роль играют потеря энергии на преодоление сил демпфирования ED и подводимая извне
энергия Еz. Если действующие в
системе силы демпфирования незначительны, то происходит переход потенциальной
энергии в кинетическую и наоборот, как в случае собственных колебаний. При автоколебаниях общее
количество энергии, переходящей из одной формы в другую, зависит также от ED и Еz . Здесь нет необходимости знать ED и Ez в каждый момент
времени t; чтобы получить общую картину колебания, вполне
достаточно знать ∆ED, т. е. потерю
энергии на преодоление сил демпфирования за период колебания, а также подводимую извне энергию ∆EZ за тот же период. Если ![]() , то
в течение каждого периода колебания энергия у системы отбирается, и происходят затухающие колебания. Если, наоборот,
, то
в течение каждого периода колебания энергия у системы отбирается, и происходят затухающие колебания. Если, наоборот, ![]() то энергия системы увеличивается, и колебания нарастают.
то энергия системы увеличивается, и колебания нарастают.
Кроме того, в [4] рассмотрены случаи, когда ∆ED и ∆EZ являются или не являются функциями амплитуды колебаний. Утверждается, что вид функции подводимой энергии ∆EZ зависит от механизма возбуждения
Цель статьи. Исследовать поведение автоколебательной системы при переходе и выходе из критического режима функционирования.
Решение задачи. Проведем анализ работы динамической системы, описываемой системой дифференциальных уравнений 1-го порядка:
|
|
(1) |
Для упрощения исследования, эту систему можно
преобразовать в одномерную динамическую систему 2-го порядка (при условии, что ![]() ), описываемую следующим
дифференциальным уравнением:
), описываемую следующим
дифференциальным уравнением:
|
|
(2) |
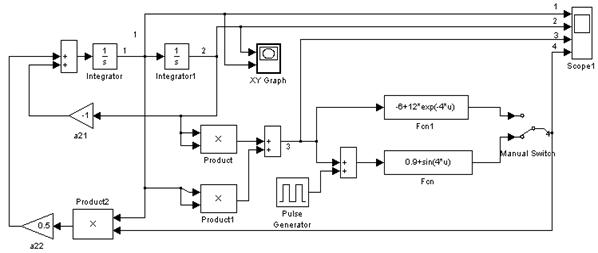
Структурная схема моделирования в программе MATLAB представлена на рис. 1.
|
|
|
Рис. 1 Схема моделирования исследуемой динамической системы. |
Диссипация энергии в системе определяется:
|
|
(3) |
При отрицательной диссипации (поглощение энергии) уравнение (3) принимает вид
|
|
(4) |
Система под действием импульсов генератора Pulse Generator переходит из одного автоколебательного режима на другой, характеризующихся различными уровнями энергии и параметрами колебаний. Переходы осуществляются при смене фронта импульса, а главное за один период колебаний системы, что доказывает квантовый характер поведения системы.
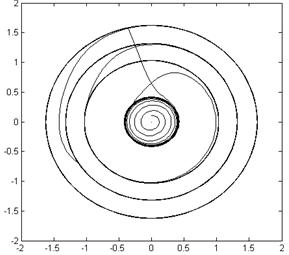
В структурной схеме предусмотрен переключатель Manual Switch. В нижнем положении ключа процесс идет по нижней ветви схемы, т.е. благодаря импульсу генератора система получает «толчок» (поглощается порция энергии), выходит из состояния устойчивых колебаний и переходит за один период колебаний на другой уровень устойчивых колебаний. Причем новый режим характеризуется большей амплитудой колебаний – на фазовом портрете (рис.2) можно проследить смену предельных циклов (от меньшего к большему). Осциллограммы интересующих сигналов представлены на рис.3.
|
|
|
Рис. 2 Фазовый портрет системы. |
|
|
|
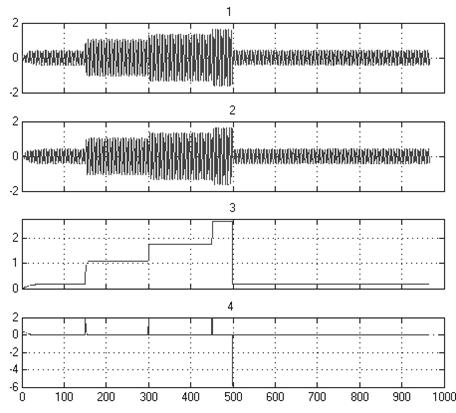
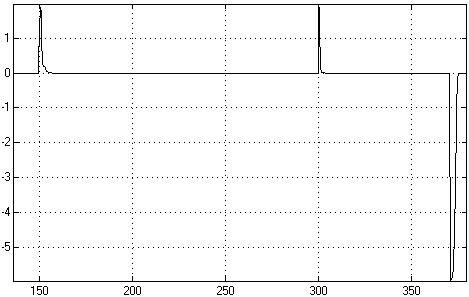
Рис. 3 Осциллограммы сигналов: 1,2 – сигналы |
Таким образом, система выполняет функции дискретного накопителя энергии.
В верхнем положении ключа процесс идет по верхней ветви схемы, что, обеспечивает изменение функции диссипации энергии:
|
|
(5) |
При этом система переходит из внешнего (конечного) предельного цикла на внутренний (начальный) предельный цикл – на фазовом портрете (рис.2) наблюдается резкая смена предельных циклов (от большего к меньшему). Следовательно, за один период колебаний система переходит в начальный режим автоколебаний, что сопровождается выделением накопленной энергии.
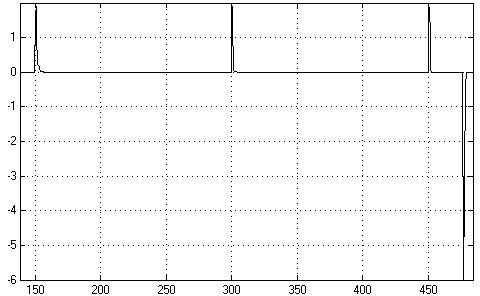
Проанализировав графики изменения количества энергии в различных режимах работы системы (рис. 4, рис. 5) можно сделать вывод, что существует возможность ударного высвобождения энергии при изменении функции диссипации.
Исследуем поведение системы, описываемой уравнением (2), в случае, когда переход в критический режим функционирования осуществляется под действием внешних колебаний. Введем звено:
|
|
(6) |
где
![]() , что обеспечивает режим автоколебаний
, что обеспечивает режим автоколебаний
|
|
|
Рис. 4. Изменение количества энергии при переходе системы со второго предельного цикла на начальный. |
|
|
|
Рис. 5 Изменение количества энергии при переходе системы с третьего предельного цикла на начальный |
В структурной схеме моделирования (рис.6) колебательное оно образовано блоками Sum1, Intefrator1, Integrator2 и множителем b2.
Введем функцию диссипации энергии в системе, описываемую уравнением (7) и имеющую вид, изображенный на рис.7.
![]() , (7)
, (7)
где
![]() .
.
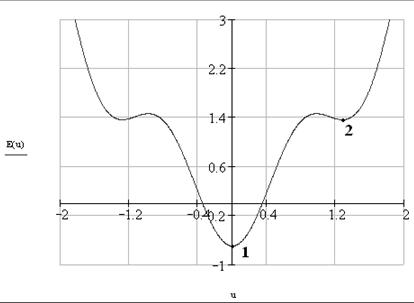
Рис.7 Вид функции, определяющей диссипацию энергии в системе.
Используя функцию такого вида можно организовать некоторую потенциальную яму, из которой система выходит под действием управления, и в которую возвращается при снятии управления (переходы из положения 1 в 2 и обратно), причем с выделением накопленной энергии
Кроме того, условия перехода системы из одного состояния в другое имеют вид:
1) ![]() - происходит
поглощение энергии;
- происходит
поглощение энергии;
2) ![]() - происходит
выделение энергии; (8)
- происходит
выделение энергии; (8)
3) ![]() -система находится
в потенциальной яме;
-система находится
в потенциальной яме;
где
![]() - действительная часть корней
характеристического уравнения исследуемой системы.
- действительная часть корней
характеристического уравнения исследуемой системы.
Таким образом, под действием резонансного звена система переходит из начального состояния в критический режим функционирования, т.е. перемещается на границу устойчивости, что сопровождается появлением предельного цикла. Существенно, что возврат на исходный цикл в этом случае осуществляется при снятии управления (при помощи Manual Switch – рис.6). Тогда система скачком, за один период колебаний переходит на внутренний предельный цикл с выделением накопленной энергии.
Описанные процессы иллюстрируют фазовый портрет системы (рис.8) и осциллограммы сигналов (рис.9)
где
![]() - действительная часть корней
характеристического уравнения исследуемой системы.
- действительная часть корней
характеристического уравнения исследуемой системы.
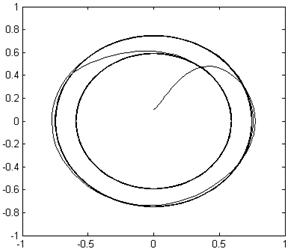
Рис. 8 Фазовый портрет системы.
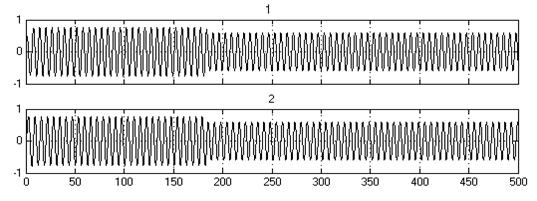
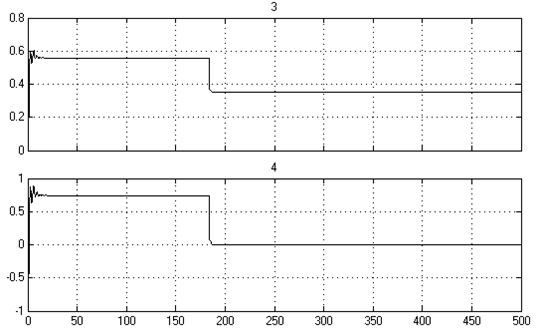
Рис. 9 Осциллограммы сигналов: 1,2 – сигналы ![]() и
и ![]() ,
показывающие колебания системы; 3 – осциллограмма, определяющая энергию в
системе; 4 – осциллограмма, показывающая изменение количества энергии при
переходе системы с одного предельного цикла на другой.
,
показывающие колебания системы; 3 – осциллограмма, определяющая энергию в
системе; 4 – осциллограмма, показывающая изменение количества энергии при
переходе системы с одного предельного цикла на другой.
|
Рис. 9 Осциллограммы сигналов: 1,2 – сигналы и , показывающие колебания системы; 3 – осциллограмма, определяющая энергию в системе; 4 – осциллограмма, показывающая изменение количества энергии при переходе системы с одного предельного цикла на другой. |
|
Таким образом, под действием резонансного звена система переходит из начального состояния в критический режим функционирования, т.е. перемещается на границу устойчивости, что сопровождается появлением предельного цикла. Существенно, что возврат на исходный цикл в этом случае осуществляется при снятии управления (при помощи Manual Switch – рис.6). Тогда система скачком, за один период колебаний переходит на внутренний предельный цикл с выделением накопленной энергии.
Описанные процессы иллюстрируют фазовый портрет системы (рис.8) и осциллограммы сигналов (рис.9)
Выводы:
1. Автоколебательные системы могут проявлять свойство накапливания энергии при переходе в критический режим функционирования.
2. Динамические системы данного класса, в случае снятия управления, выделяют всю накопленную энергию при определенном виде функции диссипации. При этом осуществляется переход с внешнего предельного цикла на внутренний предельный цикл.
3. Переход происходит за один период колебаний системы, т.е. наблюдается квантовый характер перехода.
4. Изучение критических (предельных) режимов работы данного класса систем позволит предотвратить последствия ударов в системах, возникающих при снятии управления, т.е. при резком снижении напряженности режима.
The behaviour autooscillation systems is considered when change the functions of dissipation. It is installed that turning the system from one condition in other carries the quantum nature. It is determined that when removing of management system comes out of critical mode and selects the dug energy.
1. Анищенко В.С. Сложные колебания в простых системах: Механизмы возникновения, структура и свойства динамического хаоса в радиофизических системах.- М.: Наука. Гл. ред. физ.-мат. лит., 1990. – 312 с.
2. Анищенко В.С. Устойчивость, бифуркации, катастрофы // Соросовский образовательный журнал.- 2000.- Т.6, №6. - С. 98-115.
3. Арнольд В.И. Теория катастроф.-3-е изд., доп. – М.: Наука. Гл. ред. физ.-мат.лит., 1990. – 128 с.
4. Магнус К. Колебания: Введение в исследование колебательных систем: Пер. с нем. – М.: Мир, 1982. – 304 с., ил.
5. Яворский Б.М., Детлаф А.А. Справочник по физике.- 3-е изд., испр.- М.: Наука. Гл. ред. физ.-мат. лит., 1990. – 624 с.
6. Фрадков А.Л. Кибернетическая физика: принципы и примеры. – СПб.: Наука, 2003. – 208 с., ил.
Ответы на вопросы [_Задать вопроос_]
Читайте также
Моделирование объектов и систем управления
Соколов А.Е., Махова Е.О. Моделирование процесса принятия педагогического решения при компьютеризированном обученииСлавко О.Г. Порівняльний аналіз керування регулятором на основі локальної моделі керованого процесу та П-регулятором
Войтенко В.В., Дикусар Е.В, Ситников В.С. Определение частоты среза устройства сглаживания данных на основе метода скользящего среднего
Передерій В.І. Алгоритм визначення та оцінки характеристик ефективності комп’ютерних систем на початковій стадії проектування в умовах невизначенності
Ляшенко С.А, Ляшенко А.С. Оценка модели псевдолинейной регрессии
Ладієва Л.Р. Математична модель процесу газової мембранної дистиляції
Носов П.С., Косенко Ю.І. Нечіткі моделі і методи ідентифікації та прогнозу стану інформаційної моделі студента
Китаев А.В., Глухова В.И. Анализ работы синхронного двигателя с неявнополюсным ротором по данным каталога
Дорошкевич В.К., Пироженко А.В., Хитько А.В., Хорольский П.Г. К определению требований к системам увода космических объектов
Голінко І.М., Ковриго Ю.М., Кубрак А.І. Настройка системи керування за імпульсною характеристикою об’єкта
Яшина К.В., Садовой А.В. Комплексная математическая модель тепловых процессов, происходящих в дуговых электросталеплавильных печах
Шейник С.П., Рудакова А.В. Использование функций принадлежности для моделирования параметров распределенных объектов
Хомченко А.Н., Литвиненко Е.И. Метод барицентрического усреднения граничных потенциалов электростатического поля
Селяков Е. Б. Моделирование требований к техническим системам методами математической логики
Тодорцев Ю.К., Ларіонова О.С., Бундюк А.М. Математична модель контура теплопостачання когенераційної енергетичної установки
Кириллов О.Л. , Якимчук Г.С. Моделирование процесса управления системой перегрузки углеводородных жидких топлив
Шеховцов А.Н., Козел В.Н. Построение математической модели формирования распределенных систем
Китаев А.В., Глухова В.И. Анализ поведения генератора постоянного тока по данным каталога
Хомченко А.Н., Козуб Н.О. Задачі наближення функцій: від лагранжевих до серендипових поліномів
Хобин В.А., Титлова О.А. Определение температуры парожидкостной смеси в дефлегматоре АДХМ по результатам измерений температуры его поверхности
Григорова Т.М., Усов А.В. Вероятностно-статистическое моделирование маршрутизированных пассажиропотоков в крупных городах
Горач О.О., Тернова Т.І. Моделювання технологічного процесу одержання трести при використані штучного зволоження з урахуванням складу мікрофлори
Дубік Р.М., Ладієва Л.Р. Математична модель розділення неоднорідних рідких систем
Казак В.М, Лейва Каналес Родриго, Яковицкая Е.Ю. Моделирование динамики полета магистрального самолета на исследовательском стенде
Завальнюк И.П. Исследование процесса торможения автомобиля как критического режима динамической системы
Дмитриев С.А., Попов А.В. Построение портрета неисправностей проточной части газотурбинного двигателя на примере АИ-25
Русанов С.А., Луняка К.В., Клюєв О.І., Глухов Г.М. Математичне моделювання робочого процесу в апаратах з віброкиплячим шаром та розробка систем автоматизованого моделювання гідродинаміки віброкиплячих шарів
Боярчук В.П., Сыс В.Б. Экспериментальные исследования влияния технологии шлихтования на изменение жесткости текстильных нитей
Селін Ю.М. Використовування контекстних марківських моделей для аналізу дії промислових вибухів на будівельні конструкції
Рудакова А.В. Проблемы интеграции сложных систем
Передерій В.І., Касап А.М. Математична модель та алгоритм автоматизації розрахунку параметрів комп’ютеризованих систем працюючих у реальному часі
Передерий В.И., Еременко А.П. Математические модели и алгоритмы принятия релевантных решений пользователями автоматизированных систем с учетом личностных и внешних факторов на базе генетических алгоритмов
Михайловская Т.В., Михалев А.И., Гуда А.И. Исследование правил клеточных автоматов для моделирования процессов затвердевания квазиравновесных бинарных сплавов
Хомченко А.Н., Колесникова Н.В. Явление «сверхсходимости» в задаче Прандтля для уравнения Пуассона
Китаев А.В., Глухова В.И. Анализ работы трансформатора по данным каталога
Квасницкий В.В., Ермолаев Г.В., Матвиенко М. В., Бугаенко Б.В., Квасницкий В.Ф. Оценка применимости метода компьютерного моделирования к исследованию напряженно-деформиррованного состояния цилиндрических узлов
Китаев А.И., Глухова В.И. Анализ работы асинхронного двигателя по данным каталога
Шелестов А.Ю Имитационная модель взаимодействия GRID-узлов с очередью доступа к общей памяти
Chizhenkova R.A. Mathematical Aspects of Bibliometrical Analysis of Neurophysiological Investigations of Action of Non-ionized Radiation (Medline-Internet)
Хомченко А.Н., Козуб Н.А. Геометрическое моделирование дискретных элементов с криволинейными границами
Славич В.П. Модель автоматизованої системи управління потоками транспортних засобів
Маркута О.В., Мысак В.Ф. Программная реализация и исследование особенностей метода группового учета аргументов
Степанкова Г.А., Баклан І.В. Побудова гібридних моделей на основі прихованих марківських моделей та нейронних мереж
Бакшанська Т.Д., Рижиков Ю.Г., Тодорцев Ю.К. Математична модель процесу горіння природного газу з рециркуляцією продуктів згорання для цілей управління
Хомченко А.Н. Новые решения обобщенной задачи Бюффона
Передерий В.И., Еременко А.П. Математические модели и алгоритмы определения релевантности принимаемых решений с учетом психофункциональных характеристик пользователей при управлении автоматизированными динамическими системами
Ложечников В.Ф., Михайленко В.С., Максименко И.Н. Аналитическая много режимная математическая модель динамики газовоздушного тракта барабанного котла средней мощности
Ковриго Ю.М., Фоменко Б.В., Полищук И.А. Математическое моделирование систем автоматического регулирования с учетом ограничений на управление в пакете Matlab
Исаев Е.А., Наговский Д.А. Математическое описание влияния кривизны контактирующих тел на угол смачивания жидкости в межчастичном пространстве
Бідюк П.І., Литвиненко В.І., Кроптя А.В. Аналіз ефективності функціонування мережі Байєса
Тищенко И.А., Лубяный В.З. Математическое моделирование вокодера для определения оптимальной формы импульса сигнала возбуждения.
Николаенко Ю.И., Моисеенко С.В. Моделирование гармонического полиномиального базиса гексагона.
Козуб Н.А., Манойленко Е.С., Хомченко А.Н. Температурный тест для модифицированных базисов бикубической интерполяции.
Клименко А.К. Об упрощенном численном конструировании обратной модели динамического объекта.
Китаев А.В., Сушич Е.Ф. Расчет погрешностей измерительных трансформаторов.
Передерій В.І.,Касап А.М. Математична модель та алгоритм автоматизації розрахунку параметрів комп’ютеризованих систем працюючих у реальному часі
Шпильовий Л.В. Математична модель та алгоритм екстремального управління процесом осадження дисперсної фази суспензії.
Тулученко Г.Я. Інформаційний модуль експрес-пошуку точок еквівалентності процесу нейтралізації.
Тернова Т.І. Урахування морфогенетичного рівняння в математичній моделі тканини.
Попруга А.Г. Теоретические и экспериментальные исследования электрических нагревателей по критерию экономии энергии.