УДК 681.511.4: 681.5.037

Введение. Современное производство характеризуются напряженным режимом работы оборудования, что обусловлено требованиями к эффективности технологических процессов. При этом увеличивается  вероятность переход системы в критический режим, в котором нагрузка выше номинальной [1, 2, 3], с чем связано возникновение аварийных ситуаций. В критическом режиме контур диссипации системы перегружен и теряет способность рассеивать энергию во внешнюю среду, т.е. коэффициент диссипации падает и появляется возможность накопления энергии. При неправильном управлении (естественной реакцией в такой ситуации является резкое снятие управления) энергия высвобождается в виде динамического удара в контуре диссипации создавая угрозу аварии. 

Постановка задачи. Используя модель достаточно простого  технологического аппарата, выявить условия возникновения динамического удара в контуре диссипации, путем моделирования динамики объекта оценить характер процессов, вызывающих динамический удар и выявить характер управления снижающий риск аварии при выходе из критического режима.

Анализ последних исследований и публикаций. Вопросы, связанные с особыми режимами нелинейных систем широко освещены в теории катастроф [4, 5, 6], однако в данном случае система не изменяет атрактора и не теряет устойчивости, так как при снижении диссипации просто происходит накопление энергии в системе и резко увеличивается колебательность. Так в работе [7] рассмотрено, что наряду с возмущающей силой на систему в процессе вынужденных колебаний действуют и внутренние силы колебательной системы – силы инерции, силы демпфирования и восстанавливающие силы связанные с рассеиванием энергии - диссепацией. На основе сравнения энергии, поступающей в систему за счет внешних сил  с энергией, расходуемой на преодоление демпфирования  с использованием  энергетической диаграммы показано, что если работа демпфирования меньше работы системы , то в систему посту­пает больше энергии, нежели расходуется на преодоление сил демп­фирования, и, следовательно, амплитуда увеличивается. При  потребляемая демпфированием энергия больше энергии, производимой внешней силой, и вследствие этого происходит умень­шение амплитуды. При  обе работы равны между собой: , где  - частота колебаний.

Таким образом как систуация связанная с изменением свойств системы, так и вопросы расчета режима хорошо изучены, однако для нелинейной системы с диссепацией резко уменьшающейся при привышении  энергии  системы  критического значения вопрос стратегии управления изучен слабо.

Цель статьи. Изучение поведения модели технологического аппарата как динамической системы при различном характере снятия управления в условиях работы системы в предельном режиме. А также стратегию управления, гарантирующую отсутствие ударных нагрузок в системе при выходе её из критического режима.

Решение задачи. Рассматриваемое явление носит общий характер, поэтому

исследуем простейший случай - динамическую систему второго порядка

где  ,  - функция диссипации энергии в системе.

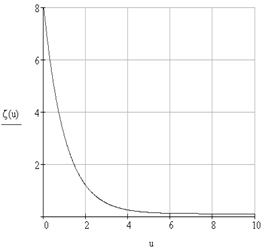
Рассмотрим наиболее простой случай - экспоненциальную зависимость диссипации энергии системы, при этом анализируемая система является нелинейной, поскольку коэффициент , определяющий затухание колебаний в системе, зависит от функции диссипации энергии в системе (рис.1):

где энергию системы оценим по фазовым переменным .

Исследуем ситуацию, когда исходное значение диссипации исключает колебательность (), а при потере диссипации, её остаточное значение очень мало (). Подчеркивая потерю эффективности контура диссипации  примем значения коэффициентов c и d в уравнении (3) равными 8 и 0.1 (соответственно).

Движение системы (1) при отсутствии управления описывается уравнением [8]:

где 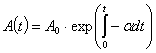, , 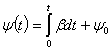 - постоянная (начальная) фаза.

Амплитуда  и частота  колебаний, по причине нелинейности системы, не являются постоянными величинами (в случае линейной системы определяются корнями характеристического уравнения - ) и могут быть определены, используя методику гармонической линеаризации нелинейных систем.

Учитывая, что во избежание  перегрузок при пуске системы, используется  постепенный разгон системы начальное управление выбираем в виде:

Амплитуда управления  обеспечивает выход системы в область малой диссипации, а постоянная времени T – больше, чем собственная потоянная времени объекта. Таким образом, выходной сигнал системы:

После завершения переходного процесса система находится в критическом состоянии и благодаря плавному разгону и выполнению условия d>0:

Следовательно, рассматриваемая система после завершения переходного процесса является системой с малой диссипацией энергии, она рассеивает энергию до определенного момента, что зависит от функции диссипации,  при дальнейшем росте управления  происходит накопление энергии – система переходит в критический режим работы. Естественно, что максимальное количество энергии зависит от амплитуды внешнего воздействия  и времени приложения управления :

Проведем анализ поведения системы при резком снятии нагрузки – естественной реакции на возникновение критического режима. Тогда управление изменяется следующим образом:

где 1(t) – ступенчатая функция.

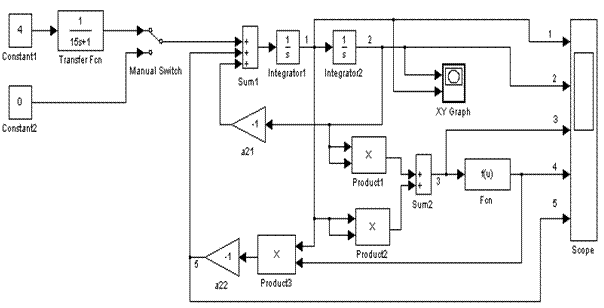
В структурной схеме моделирования (рис.2) в стандартную модель объекта 2-го порядка введен контур диссипации (Product1, Product2, Product3, Sum2, Fcn, блок а22); чтобы организовать требуемое управление (4) использованы блоки Constant1 и Transfer Fcn.

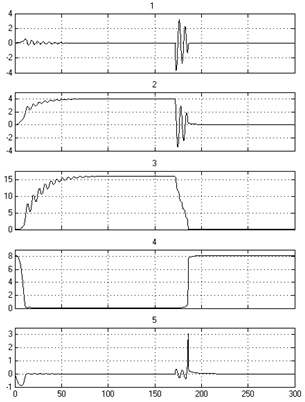
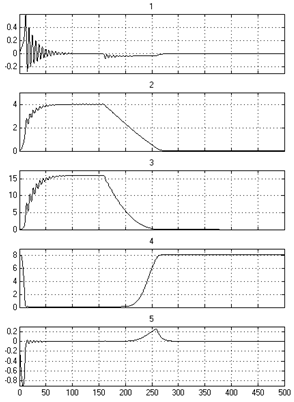
Результаты моделирования системы приведены на рис.4(а) - в системе наблюдаются высокочастотные колебания, после завершения, которых система возвращается в начальное состояние. При этом резко возрастает диссипация энергии, а в диссипирующем контуре системы происходит  удар, соответствующий мощному импульсу - за сравнительно короткий промежуток времени  выделяется накопленная энергия, что может привести к нежелательным последствиям.

Мощность удара определяется изменением энергии в системе ΔE за время Δt* прохождения участка с изменением диссипации:

где ,  - запас энергии в системе до и после снятия нагрузки

Естественно, что для исключения удара следует исключить резкое снятие управления. Поэтому управление в данном случае снимается по экспоненциальному закону, что обеспечивает рассеивание накопленной энергии до момента начала резкой диссипации. Таким образом, на спадающей части закон изменения управления будет иметь вид:

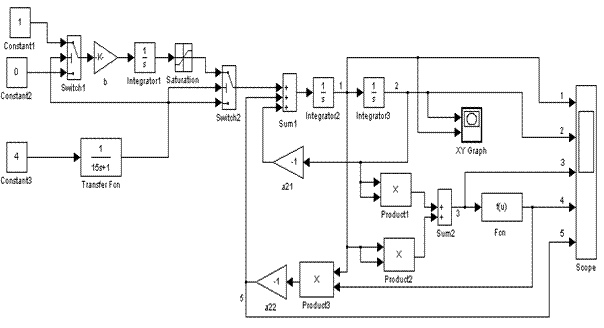
На рис.3 приведена структурная схема моделирования системы с плавным снятием управления, для чего введены блоки: Integrator1, Saturation и блок b. Важно, что длительность перехода системы в начальное состояние, длительность рассеяния энергии можно регулировать, изменяя значение коэффициента b.

Результаты моделирования системы с плавным снятием управления представлены на рис. 4(б) - система подходит к возникновению резкой диссипации плавно и амплитуда нагрузок на контур диссипации резко падает. Дополнительным фактором является  диссипация, протекающая за счет увеличения времени движения системы к границе нормального режима, для устранения удара при выходе системы из критического режима функционирования.

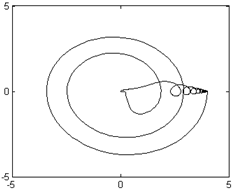
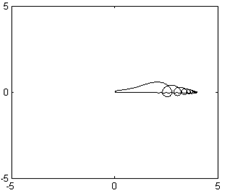
Дополнительно следует учитывать возникновение колебаний в системе. Для этого можно сравнить фазовые портреты при резком (рис. 5, а) и постепенном (рис.5, б) снятии нагрузки.

Действительно, при резком снятии управления возникают значительные колебания в системе, что легко объяснить как реакцию системы с малой диссипацией на резкое изменение управления. С другой стороны плавное снятие управления не только устраняет удар в контуре диссипации, но и резко снижает колебательность процесса остановки системы.

Выводы:

                  1.     Моделирование подтверждает гипотезу о возможности возникновения ударных нагрузок в контуре диссипации при резком снятии управления, что существенно для систем с ограниченными ресурсами контура диссипации.

                  2.     Плавный вывод систем из критического режима обеспечивает не только устранение удара, но и снижает колебательность процесса остановки системы.

                  3.     Учет изменения диссипации системы, описывает реальную ситуацию, возникающую при перенапряженных режимах, когда дальнейшая отдача энергии через контур диссипации во внешнюю среду прекращается. Например, перегрузка систем охлаждения, перенапряженность механических систем. 

                  4.     Процессы возникновения ударных нагрузок даже для простых динамических систем имеют сложный характер и требуют дальнейшего изучения.

                  1. Андронов А.А, Витт А.А, Хайкин С.Э. Теория колебаний.- 3-е изд., испр.- М.: Наука. Гл. ред. физ.-мат. лит., 1989. – 916 с.

                  2. Анищенко В.С. Сложные колебания в простых системах: Механизмы возникновения, структура и свойства динамического хаоса в радиофизических системах.- М.: Наука. Гл. ред. физ.-мат. лит., 1990. – 312 с.

                  3. Джакалья Г.Е.О. Методы теории возмущений для нелинейных систем: Пер с англ./ Под ред. А.П. Маркеева.- М.: Наука. Гл. ред. физ.-мат. лит., 1988. – 320 с.

                  4. Дж.М.Т.Томпсон Неустойчивость и катастрофы в науке и технике. Перевод с английского В.Л. Бердичевского. –М.: Мир., 1985.-254С.ил.

                  5. Тим Пост, Иэн Стюарт Теория катастроф и ее приложения. Перевод с английского А.В. Чернавского. – М.: Мир. 1980. 606С. Ил.

                  6. В.И. Арнольд Теория катастроф. -3-е изд.,доп.-М.: Наука гл.ред.физ.-мат. лит., 1990.-С.128.

                  7. Магнус К. Колебания: Введение в исследование колебательных систем: Пер. с нем. – М.: Мир, 1982. – 304 с., ил.

                  8. Теория систем автоматического регулирования, издание третье, исправленное / Бесекерский В. А., Попов Е. П. – М.: Наука, Гл. ред. физ.- мат. лит-ры, 1975. – 768 с.