УДК 532.5
Исследование устойчивости вихревых структур путем численного эксперимента
Бразалук Ю.В., Евдокимов Д.В., Поляков Н.В.
Введение. Разработка и совершенствование методов расчета вихревых течений жидкости является одним из магистральных направлений развития современной гидродинамики. Широкое распространение вихревых течений в природе и технике, важность их правильного и эффективного расчета для самых разнообразных отраслей деятельности человека определяют актуальность настоящей работы.
Современное состояние вопроса. Фундаментальной проблемой динамики вихревых течений является эволюция вихревых структур. Данному вопросу посвящена обширная литература, сколько-нибудь полный анализ которой не может быть приведен в ограниченных рамках настоящей статьи, отметим только, что достаточно полные обзоры литературы содержатся в фундаментальных монографиях по данному вопросу [1 – 5]. Определяющим фактором характера эволюции вихревой структуры является ее устойчивость, что и обусловило значительный интерес к этому вопросу, отраженный в упоминавшихся уже монографиях [1 – 5]. Трактовка понятия устойчивость в гидродинамике обычно несколько шире, нежели традиционная асимптотическая устойчивость по Ляпунову, используемая в теории дифференциальных уравнений. Гидродинамически устойчивой будем называть систему, которая сохраняет свои параметры в пределах определенных интервалов в течение некоторого конечного промежутка времени.
К сожалению, задачи об эволюции вихревой структуры имеет аналитическое решение только в очень ограниченном числе случаев [6]. В общем случае она может быть решена только численно. Как эйлеровы, так и лагранжевы подходы могут быть использованы при численном расчете, однако с ростом числа Рейнольдса применение эйлеровых подходов, например, метода конечных разностей, вызывает все больше затруднений, в результате чего в [2] высказана мысль о возможной неэффективности метода конечных разностей для численного решения подобных задач. Отметим, что большинство попыток численного анализа подобных задач было выполнено при помощи лагранжевых методов [1, 2, 4, 6 – 15]. Традиционно рассматривают плоские вихревые структуры, поскольку пространственный анализ в подобных задачах затруднен большим расходом ресурсов ЭВМ и сложностью визуализации, хотя принципиально пространственный анализ вполне возможен. В настоящей работе рассмотрение также будет ограничено плоским случаем.
По результатам вычислительного эксперимента можно судить не о собственно гидродинамической устойчивости, а о вычислительной устойчивости вихревой структуры, то есть, помимо гидродинамической неустойчивости может иметь место и неустойчивость вычислительного процесса. Неустойчивость вычислительного процесса, как правило, является следствием использования конкретной аппроксимации, например, дискретных вихрей. Хотя в работах [2, 3, 5, 6, 13, 14] и делались попытки ввести в схемы метода дискретных вихрей вязкую диссипацию, проблема эквивалентности расчетных схем в целом остается далекой от полного разрешения. Однако для конечных и относительно небольших промежутков времени и при достаточно больших числах Рейнольдса расчет эволюции вихревых структур методом дискретных вихрей дает результаты достаточно близкие реальным течениям, то есть, можно надеяться, что для таких случаев понятие гидродинамической устойчивости и вычислительной устойчивости также будут соответствовать друг другу.
Следует отметить, что существует известное расхождение во взглядах на проблему устойчивости. Дело в том, что системы, включающие 4 и более дискретных вихрей, начиная с некоторого момента времени, демонстрируют хаотическое поведение [2, 16] , то есть, асимптотически неустойчивы по Ляпунову. Однако многие системы дискретных вихрей, будучи неустойчивыми по Ляпунову, демонстрируют явно выраженную вычислительную устойчивость, которая, как отмечалось выше, как правило, соответствует гидродинамической устойчивости.
Нерешенные задачи и цели настоящей работы. Принципиальным недостатком метода дискретных вихрей является некорректное представление скоростей вихря при межвихревом взаимодействии на малом расстоянии. Для преодоления этой трудности используются различные схемы регуляризации [3, 17], которые, однако, решают проблему лишь частично. В работах [7, 17] предложен другой путь разрешения указанной проблемы – замена пары близкодействующих вихрей комбинацией вихря и вихревого диполя. Исходя из вышесказанного, первой целью настоящей работы является анализ устойчивости дипольно-вихревых структур путем численного эксперимента методом дискретных особенностей (дискретных вихрей и диполей), в отличие от предыдущих работ, где на устойчивость исследовались чисто вихревые структуры. Второй целью настоящей работы является исследование влияния дискретно-вихревой аппроксимации на потерю симметрии и последующую потерю устойчивости «больших» вихревых структур. В целом, следует отметить, что количество работ, в которых исследовались свойства «больших» вихревых структур, получающихся в результате дискретно-вихревой аппроксимации распределенной в области завихренности, весьма ограничено [2, 3, 6, 13, 14].
Постановка задачи. В отличие от классических работ по методу дискретных вихрей, где были даны формулировки задачи в терминах завихренность - скорость, в настоящей работе задача будет сформулирована в терминах завихренность - функция тока, следуя работе [17]. Функция тока плоского течения несжимаемой жидкости удовлетворяет следующему интегральному соотношению [17]:
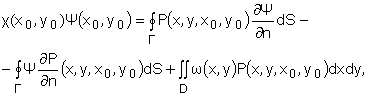 (1)
(1)
где ![]() – распределенная завихренность,
– распределенная завихренность, ![]() – область течения (в нашем случае
– область течения (в нашем случае ![]() ),
), ![]() –
граница области
–
граница области ![]() , поскольку область
бесконечная, то первые два интеграла в (1) выпадают, функции
, поскольку область
бесконечная, то первые два интеграла в (1) выпадают, функции
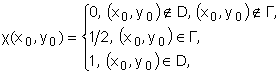
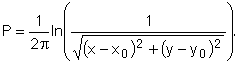
Метод дискретных вихрей предполагает представления завихренности в виде
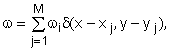 (2)
(2)
где ![]() – количество дискретных вихрей,
– количество дискретных вихрей, ![]() – их интенсивности. Тогда
– их интенсивности. Тогда
![]() (3)
(3)
Формально для комбинированного представления дискретных вихрей и дискретных диполей представление (2) должно быть заменено следующим представлением:
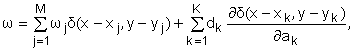 (4)
(4)
где ![]() – ось соответствующего диполя,
– ось соответствующего диполя, ![]() – его интенсивность. Однако
представление (4) лишено физического смысла, поэтому, следуя работам [7, 17] ,
примем в качестве исходного следующее представление для функции тока
– его интенсивность. Однако
представление (4) лишено физического смысла, поэтому, следуя работам [7, 17] ,
примем в качестве исходного следующее представление для функции тока
![]() (5)
(5)
опустив для краткости его вывод, который полностью соответствует приведенному в работах [7, 17]. Тогда поля скоростей
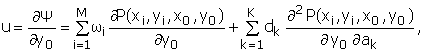 (6а)
(6а)
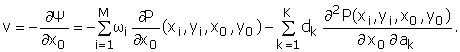 (6б)
(6б)
Как обычно, предполагаем, что вихри и диполи не влияют на величину скорости в точках, где они расположены. На вопросах регуляризации поля скоростей останавливаться не будем, поскольку они подробно изложены в работах [2, 3, 17].
Движение дискретных вихрей и диполей описывается системой
![]() (7)
(7)
Подставляя в (7) представления для скоростей (6), получим систему из М+К обыкновенных дифференциальных уравнений, которую дополним следующими начальными условиями:
![]() (8)
(8)
Метод решения. Задача Коши (7), (8) может быть решена любым из существующих методов численного решения систем обыкновенных дифференциальных уравнений. Приведенные ниже расчеты проведены при помощи метода Эйлера, то есть, использовалась следующая схема:
![]() (9)
(9)
Результаты расчетов. На основании приведенных выше формулировок задач (6) – (8) и численного алгоритма (9) были проведены несколько серий расчетов эволюции вихревых структур, аппроксимированных дискретными вихревыми и дипольно-вихревыми системами. Контроль устойчивости вихревых структур производился визуально на основании анализа траекторий дискретных особенностей. Каждый расчет проверялся контрольным расчетом с половинным шагом по времени, для ряда расчетов были проведены контрольные с более подробной аппроксимацией.
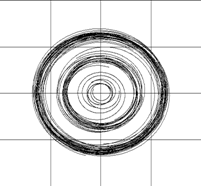
На качественном уровне можно выделить три состояния вихревых структур: устойчивая структура, неустойчивая структура и структура, устойчивая «как облако», то есть сохраняющая свою форму, но изменяющая размеры (термин заимствован в зарубежной литературе [5] и, возможно, является не совсем удачным).
Все рассмотренные в расчетах вихревые и дипольно-вихревые структуры имели первоначальную центральную симметрию, что обеспечивало их устойчивость для начальных моментов времени.
Выводы. По результатам проведенных расчетов можно сделать следующие выводы
1. Потеря устойчивости симметричной структуры происходит по следующей схеме: устойчивая структура; структура, устойчивая «как облако»; неустойчивые структуры. Причем в течение достаточно долгого времени неустойчивость проявляется в том, что отдельные вихри покидают структуру, остальная же часть структуры сохраняет устойчивость «как облако».
2. Более интенсивные (с большей плотностью завихренности) структуры разрушаются быстрее.
3. Мощный центральный вихрь ухудшает устойчивость структуры, но структура с концентрированным центральным вихрем более устойчива, чем структура с распределенной эквивалентной завихренностью.
4. Даже относительно слабый центральный диполь резко ухудшает устойчивость вихревой структуры.
5. Дипольно-вихревые структуры теряют устойчивость намного быстрее аналогичных вихревых, даже при слабых диполях. Следует отметить, что влияние диполей является важным и часто определяющим механизмом потери устойчивости.
6. Из всех исследованных структур наиболее устойчивой оказалось вихревое кольцо, это дает основание считать, что вихревое кольцо является наиболее устойчивой вихревой структурой вообще.
|
|
|
|
а) |
б) |
|
|
|
|
в) |
г) |
|
|
|
|
д) |
|
|
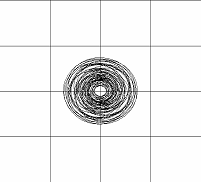
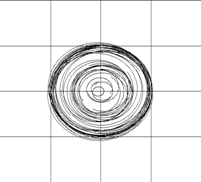
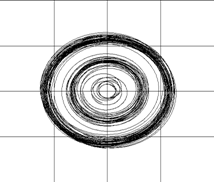
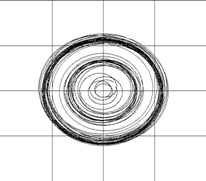
Рис. 1. Эволюция круговой вихревой структуры, устойчивой «как облако». На рисунках г) и д) отчетливо видно, что завихренность образует вихревые кольца, которые являются более устойчивыми вихревыми структурами |
|
|
|
|
|
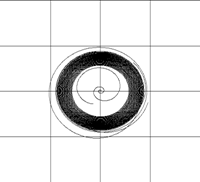
Рис. 2. Потеря симметрии вихревого кольца из-за сильного центрального вихря |
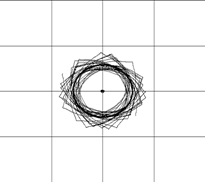
Рис. 3. Разрушение вихревого кольца центральным диполем |
Полученные в настоящей статье результаты имеют существенное методологическое значения для гидродинамики вихревых течений, поскольку здесь рассмотрена фундаментальная задача эволюции и устойчивости вихревых структур. Результаты работы могут быть использованы для разработки эффективных методик расчета вихревых течений, например, выявления когерентных структур в турбулентных течениях.
Разумеется, проблема устойчивости вихревых структур не исчерпывается настоящей работой. Остаются нерешенными многочисленные вопросы, связанные с взаимодействием вихревых структур между собой, образованием в результате взаимодействия новых устойчивых вихревых структур, взаимодействием вихревых структур с другими объектами в потоке и т.д. Остались недостаточно исследованными ряд задач, связанных с внутренними проблемами эволюции вихревых и дипольно-вихревых структур, например, проблема эквивалентности эффектов схемной вязкости эффектам вязкой диссипации, проблема эволюции диполей. Однако развитый в настоящей работе подход позволяет надеяться на эффективное разрешение указанных задач в будущих исследованиях.
The article is devoted to research of stability of vortical structures by the numeral experiment
1. Вилля Г. Теория вихрей. – Л.; М.: ОНТИ, 1936. – 268 с.
2. Белоцерковский С.М., Гиневский А.С. Моделирование турбулентных струй и следов на основе метода дискретных вихрей. – М.: Издательская фирма «Физико-математическая литература», 1995. – 368 с.
3. Белоцерковский С.М., Котовский В.Н., Ништ М.И., Федоров П.М. Математическое моделирование плоскопараллельного отрывного обтекания тел. – М.: Наука, 1988. – 309 с.
4. Салтанов Н.В., Горбань В.А. Вихревые структуры в жидкости: аналитические и численные решения. – К.: Наукова думка, 1993. – 244 с.
5. Chorin, A.J. Vorticity and Turbulence. – Springer-Verlag, Berlin, New York, 1994.
6. Евдокимов Д.В., Найденова М.А., Поляков Н.В. К вопросу о моделировании диффузии завихренности в граничноинтегральных методах вычислительной гидродинамики // Труды института прикладной математики и механики НАН Украины – Донецк, 2001. - Т. 6. - С. 39-43.
7. Бразалук Ю.В., Евдокимов Д.В., Поляков Н.В. Применение комбинированного метода граничных элементов и дискретных вихрей для решения некоторых задач гидродинамического взаимодействия в плоских потоках // Вестник Харьковского национального университета. Сер. «Математическое моделирование. Информационные технологии. Автоматизированные системы управления». – 2003. - Вып. 1, № 590. – С. 55-60.
8. Веретенцев А.Н., Гешев П.И, Рудяк В.Я. О развитии метода вихревых частиц применительно к описанию отрывных течений // Журн. вычисл. математики и мат.физики.. – 1989.. – Т. 29, № 6. – С. 878-887.
9. Веретенцев А.Н., Рудяк В.Я. О процессах образования и эволюции вихревых структур в сдвиговых слоях // Изв. АН СССР. Механика жидкости и газа. – 1987. – №1. – С.31-37.
10. Веретенцев А.Н., Рудяк В.Я., Яненко Н.Н. Построение дискретных вихревых моделей течений идеальной несжимаемой жидкости // Журн. вычисл. математики и мат. физики. – 1986. – Т. 26, № 1. – С. 103-113.
11. Белоцерковский С.М., Лифанов И.К. Численные методы в сингулярных интегральных уравнениях. – М.: Наука, 1985. – 253 с.
12. Белоцерковский С.М., Ништ М.И. Отрывное и безотрывное обтекание тонких крыльев идеальной жидкостью. – М.:Наука, 1978.–351 с.
13. Сарпкайя Т. Вычислительные методы вихрей // Тр. Американского об-ва инженеров механиков. Сер. А. – 1989. – № 10. – С. 1-60.
14. Сарпкайя Т., Шоафф Р.Л. Невязкая модель образования двухмерных вихрей за круговым цилиндром // Ракет. техника и космонавтика. – 1979. – Т. 17, № 11. – С. 51–60.
15. Chorin A.J., Bernard P.S. Discretization of Vortex Sheet with an Example of Roll-up // J. Computational. Physic. – 1973. – V. 13. – P. 423-429.
16. Aref H. Integrable, chaotic and turbulent vortex motion in two-dimensional flows // Ann. rev. fluid mech. – 1983. – V. 15. – P. 345-389.
17. Yevdokymov D. V. Boundary element and discrete vortices method for ideal fluid flow calculations. // D. Durban and A. R. J. Pearson (Eds.) Non-linear singularities in deformation and flow. Proceeding of IUTAM Symposium held in Haifa, Israel, 17-21 March, 1997. Kluwer Academic Publisher. – P. 217-230.
Ответы на вопросы [_Задать вопроос_]
Читайте также
Моделирование объектов и систем управления
Соколов А.Е., Махова Е.О. Моделирование процесса принятия педагогического решения при компьютеризированном обученииСлавко О.Г. Порівняльний аналіз керування регулятором на основі локальної моделі керованого процесу та П-регулятором
Войтенко В.В., Дикусар Е.В, Ситников В.С. Определение частоты среза устройства сглаживания данных на основе метода скользящего среднего
Передерій В.І. Алгоритм визначення та оцінки характеристик ефективності комп’ютерних систем на початковій стадії проектування в умовах невизначенності
Ляшенко С.А, Ляшенко А.С. Оценка модели псевдолинейной регрессии
Ладієва Л.Р. Математична модель процесу газової мембранної дистиляції
Носов П.С., Косенко Ю.І. Нечіткі моделі і методи ідентифікації та прогнозу стану інформаційної моделі студента
Китаев А.В., Глухова В.И. Анализ работы синхронного двигателя с неявнополюсным ротором по данным каталога
Дорошкевич В.К., Пироженко А.В., Хитько А.В., Хорольский П.Г. К определению требований к системам увода космических объектов
Голінко І.М., Ковриго Ю.М., Кубрак А.І. Настройка системи керування за імпульсною характеристикою об’єкта
Яшина К.В., Садовой А.В. Комплексная математическая модель тепловых процессов, происходящих в дуговых электросталеплавильных печах
Шейник С.П., Рудакова А.В. Использование функций принадлежности для моделирования параметров распределенных объектов
Хомченко А.Н., Литвиненко Е.И. Метод барицентрического усреднения граничных потенциалов электростатического поля
Селяков Е. Б. Моделирование требований к техническим системам методами математической логики
Тодорцев Ю.К., Ларіонова О.С., Бундюк А.М. Математична модель контура теплопостачання когенераційної енергетичної установки
Кириллов О.Л. , Якимчук Г.С. Моделирование процесса управления системой перегрузки углеводородных жидких топлив
Шеховцов А.Н., Козел В.Н. Построение математической модели формирования распределенных систем
Китаев А.В., Глухова В.И. Анализ поведения генератора постоянного тока по данным каталога
Хомченко А.Н., Козуб Н.О. Задачі наближення функцій: від лагранжевих до серендипових поліномів
Хобин В.А., Титлова О.А. Определение температуры парожидкостной смеси в дефлегматоре АДХМ по результатам измерений температуры его поверхности
Григорова Т.М., Усов А.В. Вероятностно-статистическое моделирование маршрутизированных пассажиропотоков в крупных городах
Горач О.О., Тернова Т.І. Моделювання технологічного процесу одержання трести при використані штучного зволоження з урахуванням складу мікрофлори
Дубік Р.М., Ладієва Л.Р. Математична модель розділення неоднорідних рідких систем
Казак В.М, Лейва Каналес Родриго, Яковицкая Е.Ю. Моделирование динамики полета магистрального самолета на исследовательском стенде
Завальнюк И.П. Исследование процесса торможения автомобиля как критического режима динамической системы
Дмитриев С.А., Попов А.В. Построение портрета неисправностей проточной части газотурбинного двигателя на примере АИ-25
Русанов С.А., Луняка К.В., Клюєв О.І., Глухов Г.М. Математичне моделювання робочого процесу в апаратах з віброкиплячим шаром та розробка систем автоматизованого моделювання гідродинаміки віброкиплячих шарів
Боярчук В.П., Сыс В.Б. Экспериментальные исследования влияния технологии шлихтования на изменение жесткости текстильных нитей
Селін Ю.М. Використовування контекстних марківських моделей для аналізу дії промислових вибухів на будівельні конструкції
Рудакова А.В. Проблемы интеграции сложных систем
Передерій В.І., Касап А.М. Математична модель та алгоритм автоматизації розрахунку параметрів комп’ютеризованих систем працюючих у реальному часі
Передерий В.И., Еременко А.П. Математические модели и алгоритмы принятия релевантных решений пользователями автоматизированных систем с учетом личностных и внешних факторов на базе генетических алгоритмов
Михайловская Т.В., Михалев А.И., Гуда А.И. Исследование правил клеточных автоматов для моделирования процессов затвердевания квазиравновесных бинарных сплавов
Хомченко А.Н., Колесникова Н.В. Явление «сверхсходимости» в задаче Прандтля для уравнения Пуассона
Китаев А.В., Глухова В.И. Анализ работы трансформатора по данным каталога
Квасницкий В.В., Ермолаев Г.В., Матвиенко М. В., Бугаенко Б.В., Квасницкий В.Ф. Оценка применимости метода компьютерного моделирования к исследованию напряженно-деформиррованного состояния цилиндрических узлов
Китаев А.И., Глухова В.И. Анализ работы асинхронного двигателя по данным каталога
Шелестов А.Ю Имитационная модель взаимодействия GRID-узлов с очередью доступа к общей памяти
Chizhenkova R.A. Mathematical Aspects of Bibliometrical Analysis of Neurophysiological Investigations of Action of Non-ionized Radiation (Medline-Internet)
Хомченко А.Н., Козуб Н.А. Геометрическое моделирование дискретных элементов с криволинейными границами
Славич В.П. Модель автоматизованої системи управління потоками транспортних засобів
Маркута О.В., Мысак В.Ф. Программная реализация и исследование особенностей метода группового учета аргументов
Степанкова Г.А., Баклан І.В. Побудова гібридних моделей на основі прихованих марківських моделей та нейронних мереж
Бакшанська Т.Д., Рижиков Ю.Г., Тодорцев Ю.К. Математична модель процесу горіння природного газу з рециркуляцією продуктів згорання для цілей управління
Хомченко А.Н. Новые решения обобщенной задачи Бюффона
Передерий В.И., Еременко А.П. Математические модели и алгоритмы определения релевантности принимаемых решений с учетом психофункциональных характеристик пользователей при управлении автоматизированными динамическими системами
Ложечников В.Ф., Михайленко В.С., Максименко И.Н. Аналитическая много режимная математическая модель динамики газовоздушного тракта барабанного котла средней мощности
Ковриго Ю.М., Фоменко Б.В., Полищук И.А. Математическое моделирование систем автоматического регулирования с учетом ограничений на управление в пакете Matlab
Исаев Е.А., Наговский Д.А. Математическое описание влияния кривизны контактирующих тел на угол смачивания жидкости в межчастичном пространстве
Бідюк П.І., Литвиненко В.І., Кроптя А.В. Аналіз ефективності функціонування мережі Байєса
Тищенко И.А., Лубяный В.З. Математическое моделирование вокодера для определения оптимальной формы импульса сигнала возбуждения.
Николаенко Ю.И., Моисеенко С.В. Моделирование гармонического полиномиального базиса гексагона.
Козуб Н.А., Манойленко Е.С., Хомченко А.Н. Температурный тест для модифицированных базисов бикубической интерполяции.
Клименко А.К. Об упрощенном численном конструировании обратной модели динамического объекта.
Китаев А.В., Сушич Е.Ф. Расчет погрешностей измерительных трансформаторов.
Передерій В.І.,Касап А.М. Математична модель та алгоритм автоматизації розрахунку параметрів комп’ютеризованих систем працюючих у реальному часі
Шпильовий Л.В. Математична модель та алгоритм екстремального управління процесом осадження дисперсної фази суспензії.
Тулученко Г.Я. Інформаційний модуль експрес-пошуку точок еквівалентності процесу нейтралізації.
Тернова Т.І. Урахування морфогенетичного рівняння в математичній моделі тканини.
Попруга А.Г. Теоретические и экспериментальные исследования электрических нагревателей по критерию экономии энергии.