Автоматика.
    Автоматизация.
        Электротехнические
            комплексы и системы.

УДК 007

КОЛИЧЕСТВЕННЫЙ ПОДХОД К ПОДБОРУ СОТРУДНИКОВ

ДЛЯ КОЛЛЕКТИВНОЙ ДЕЯТЕЛЬНОСТИ

Кирюшатова Т.Г.

В любой сфере общественной жизни с полной отдачей и добросовестно будут работать люди действительно попавшие «на своё место», а задача расставить людей так, чтобы они работали добросовестно и с полной отдачей, исключительно сложна. С задачами распре­деления функций в совместной деятельности повсеместно и посто­янно сталкиваются в своей практике и руководители различных уровней, и сами коллективы.

Все участвующие в этих процессах лица знают, что решать эти задачи надо для достижения определенных целей: выполнения плана, получения результата, осуществления деятельности как таковой, но в то же время и для обеспечения удовлетворенности членов коллектива своим трудом, получения заслуженного вознаграждения за свой вклад в общее дело, созда­ния благоприятных отношений в коллективе, поддержания нор­мальных условий совместной деятельности и т. д. Очевидно, что этот процесс обусловлен рядом факторов при решении этих задач, приходится учитывать разные обстоятельства: наличие нужных работников, их запросы, возможные распоряжения администра­ции, многочисленные конкретные условия и т. д. Возможно действие и таких факторов, как различные виды группового давления, протекционизм, внеслужебные, неделовые соображения и т. д. И результаты решения задач распределения функций можно оценить по-разному, например однопланово — при учете лишь конечного результата или многопланово и неоднозначно — с ориентацией на разнообразные аспекты проблемы, с учетом раз­личных отношений и параметров.

Для этого очень важно правильно распределить функции между субъектами производственной деятельности. Субъектами, выполняющими эту деятельность, могут быть отдельные лица или группа лиц в системе управления или в основном производстве. Субъекты могут различаться по месту в системе (статусу, рангу, позиции), по признаку коллективности (отдельное лицо, занимающее конкретную позицию в системе деятельности, или группа) и включенности в сам процесс (распре­деление может производиться лицом, стоящим вне системы функ­ций, подлежащих распределению, или осуществляется самой груп­пой, например бригадой, которая затем будет выполнять эти функции).

В настоящее время повышение эффективности функционирования человеко-машинных систем идет по трем направлениям:

-повышение эффективности работы «машинной части» путем улучшения характеристик машин и технологии;

-повышение эффективности работы человека-оператора или группы операторов;

-нахождение оптимальных соотношений между «человеческой» и «машинной» частями.

Третьим направлением, менее всего разработанным для практических задач и определяющим одно из основных звеньев систем управления, интенсивно занимаются специалисты по управлению и математики.

При коллективной деятельности операторов могут возникать нестандартные ситуации, отличные от штатной деятельности: работа неполным составом смены, замена отдельных ее членов менее квалифицированными операторами, частичная потеря трудоспособности отдельными операторами и наиболее сложная ситуация-работа при наличии конфликта. Все это приводит к снижению общей производительности работы коллектива и увеличивает вероятность ошибок.

Вероятность развития конфликта в группе зависит от типов составляющих ее отдельных личностей и направленности их целей: на себя, на коллектив, на дело.[1]

Суть конфликта для нового члена группы - изменить ценности других в свою пользу, увеличить свою ценность по сравнению с ценностью руководителя или задач группы.

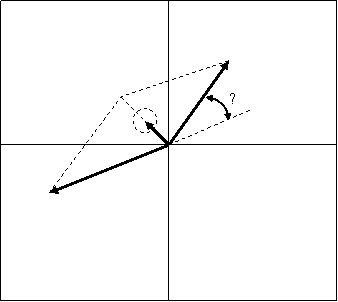
Согласно гипотезе Р.Акоффа [2], основой для оценки вероятности конфликтности группы должны служить матрицы координат каждого из операторов данной группы в пространстве личности (рис.1) в котором ось абсцисс «Х» («интернализация-экстернализация») отражает степень влияния человека на окружение, а ось ординат «У» («объективерсия-субъективерсия») - степень чувствительности личности к окружению. Координаты Х и У индивидуума обычно находят с помощью экспертных оценок пяти независимых экспериментаторов.

 Предлагается количественная методика определения матрицы координат индивидуума в пространстве личности как функции шестнадцати параметров, получаемых в результате обработки теста Кэттэла [3]

X_i=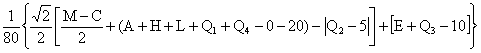   (1)

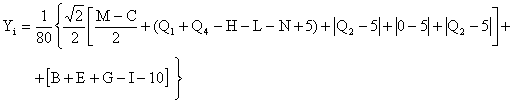
где  A,B,C,D,E,F,G,H,I,L,M,N,O,Q₁,Q₂,Q₃,Q₄- величина параметров личности по соответствующим шкалам Кэттэла в стандартных стенах.

Во введенном пространстве личность индивида рассматривается как сила, величина которой пропорциональна удалению точки, соответствующей этому индивиду от точки (0;0)- начала координат, так называемой  «точки центроверсии».

                                                                            Y

                                                                                      В

объективерсия

                                                       Д

                                                               Z           Ө

                                                                                                                             X

                                                                      О

                                         А

субъективерсия

                                           интернализация              экстернализация

Рис. 1

Коллектив из двух операторов А и В обладает  силой ОZ, равной векторной полусумме сил ОА и ОВ, соответствующих каждому из индивидов. Таким образом, построив параллелограмм АОВД на ОА и ОВ как на сторонах и взяв половину его диагонали OZ=1/2ОД (1/2-коэфициент нормировки, применяемый для того, чтобы результирующий вектор сил не выходил за пределы пространства личности). В общем случае для коллектива из s операторов  абсолютная величина результирующей силы |d_s| равна:

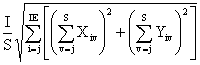=                                     (2)

где       i - число шкал Кэттэла, принимаемых к рассмотрению,

v - количество операторов в коллективе.

Пара, вектор результирующей силы который расположен в точке центроверсии или недалеко от нее, легко распределяет психологическую нагрузку и может эффективно сотрудничать. Чем  дальше от центроверсии сила пары OZ, тем острее становится соперничество (конфликт) из-за выполнения одной и той же психологической функции. Увеличиваются искажения в восприятии одного лица другим.

Под восприятием мы понимаем то расположение, которое по убеждению одного лица свойственно другому в пространстве личности.

Искажения в восприятии характеризуются углом асимметрии «θ»  (рис. 1) между векторами сил пары или коллектива и новичка.

Когда угол асимметрии превышает 90°, партнеры постепенно теряют надежду на возможность перемен и конфликт приобретает затяжной характер.

Таким образом, с целью предотвращения конфликтных ситуаций в результате замены выбывшего оператора подбирать нового члена группы надо так, чтобы угол асимметрии «Ө»  между вектором оставшихся членов группы и новичком и абсолютная величина вектора результирующей силы новой группы |d_si| были минимальными. Для  этого необходимо иметь картину «устойчивости» коллектива в виде матриц (тензоров) «неравновесия» и «асимметрии»,  на основе которых можно проводить имитационные эксперименты.

1.                  Разработка методов математической формализации деятельности коллективов операторов различной численности в условиях помех и дефицита  времени: Отчет о НИР / КПИ им. С. Лазо; руководитель работы Марсанов В.В. , №  ГР 01.  8.80.084062. – Кишинев, 1989.

2.                  Акофф Р. , Эмерли Ф. О целеустремленных системах. – М. : Советское радио, 1974.

3.                  Мельников В.М. , Ямпольский Л.Т. Введение в экспериментальную психологию личности. – М. : Просвещение, 1985.

4.                  Трофимов Ю.Л. Инженерная психология. – «Либiдь», 2002. – 264 с.

5.                  Уинстон П. Искусственный интеллект. – М. : Наука, 1980. – 520 с.